Bài toán về nghiệm của phương trình với tham số SVIP

Cho hàm số $y = f(x)$ có đạo hàm trên $\mathbb{R}$ và có bảng biến thiên như hình vẽ

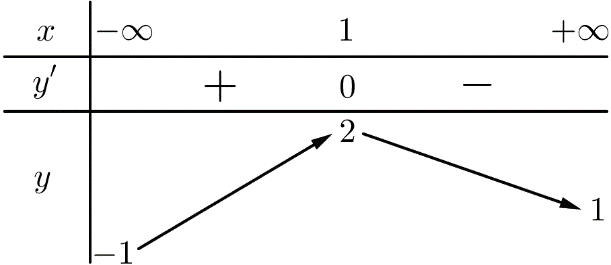
Phương trình $f(x) = m$ có $2$ nghiệm thực phân biệt khi và chỉ khi

Cho hàm số $y = f(x)$ xác định, liên tục trên $\mathbb{R}$ và có bảng biến thiên sau:

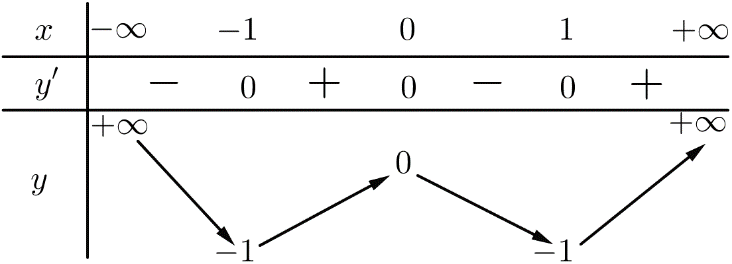
Giá trị của tham số $m$ để phương trình $f(x) - 1 = m$ có $2$ nghiệm là

Cho hàm số $y = f(x)$ xác định trên $\mathbb{R}\backslash\left\{ 2 \right\},$ liên tục trên mỗi khoảng xác định và có bảng biến thiên sau:

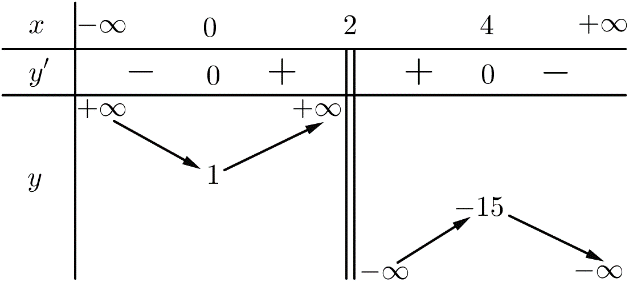
Tập hợp các giá trị thực của tham số $m$ để phương trình $f(x) + m = 0$ có nhiều nghiệm thực nhất là

Cho hàm số $y = f(x)$ xác định trên $\mathbb{R}\backslash\left\{ 1 \right\},$ liên tục trên từng khoảng xác định và có bảng biến thiên như sau:

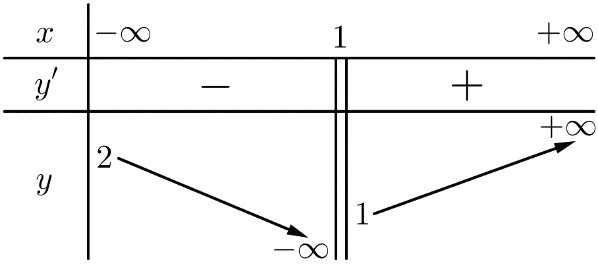
Giá trị thực của tham số $m$ để đồ thị hàm số $y = f(x)$ cắt đường thẳng $y = 2m - 1$ tại hai điểm phân biệt là

Cho hàm số $y = f(x)$ xác định trên $\mathbb{R}\backslash\left\{ - \ 1;1 \right\},$ liên tục trên mỗi khoảng xác định và có bảng biến thiên sau:

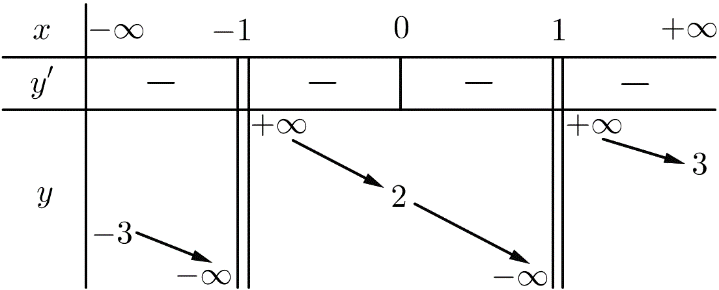
Giá trị của tham số $m$ để đường thẳng $y = 2m + 1$ cắt đồ thị hàm số đã cho tại hai điểm phân biệt là

Cho hàm số $y = f(x)$ xác định trên $\mathbb{R}\backslash\left\{ 0 \right\},$ liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:

Tập hợp các giá trị của tham số $m$ để phương trình $f(x) = m$ có ba nghiệm thực phân biệt là

Cho hàm số $y = f(x)$ xác định trên $\mathbb{R}\backslash\left\{ - 1 \right\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:

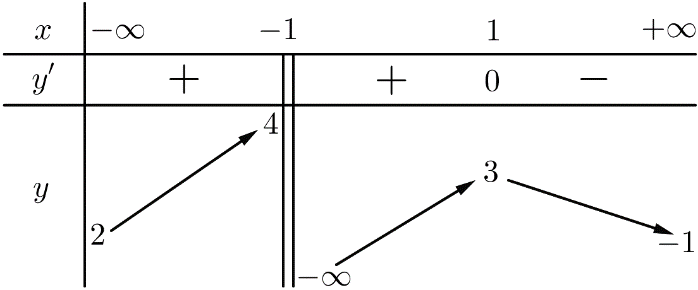
Có bao nhiêu giá trị nguyên của tham số $m$ thuộc $\lbrack - 5;5\rbrack$ để phương trình $f(x) = m$ có nghiệm duy nhất?

Cho hàm số $y = f(x)$ xác định trên $\mathbb{R}\backslash\left\{ \pm \ 1 \right\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:

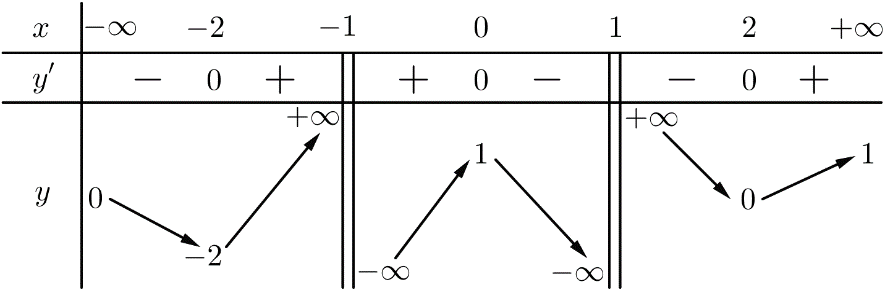
Có bao nhiêu giá trị nguyên của tham số $m$ để phương trình $f(x) = m$ có $4$ nghiệm phân biệt?

Tìm tất cả các giá trị của tham số $m$ để phương trình $- x^{4} + 2x^{2} - m=0$ có bốn nghiệm phân biệt.

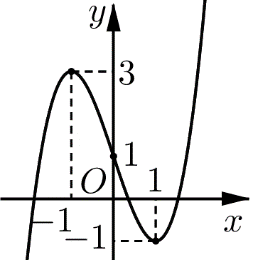
Cho hàm số bậc ba $y = f(x)$ có đồ thị như hình vẽ bên. Giá trị thực của tham số $m$ để phương trình $f(x) + m - 2020 = 0$ có nghiệm duy nhất là

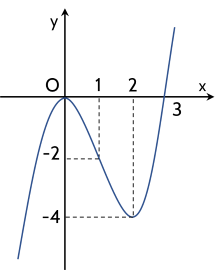
Cho hàm số $y = x^{3} - 3x^{2}$ có đồ thị như hình vẽ. Giá trị của tham số $m$ để phương trình $x^{3} - 3x^{2} + 3m - 1 = 0$ có ba nghiệm phân biệt trong đó có đúng hai nghiệm lớn hơn $1$ là

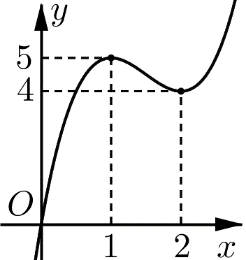
Cho hàm số $y = f(x) = \ 2x^{3} - 9x^{2} + 12x$ có đồ thị như hình vẽ. Giá trị của tham số $m$ để phương trình $\text{\ f}\left( |x| \right) + m = 0$ có $6$ nghiệm phân biệt là

Cho hàm số bậc ba $y = f(x)$ có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số $m$ để phương trình $2\left| f(x) \right| - m = 0$ có $4$ nghiệm phân biệt?

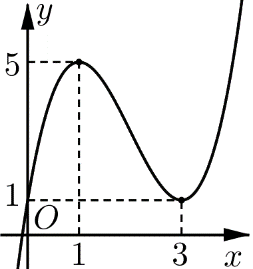
Cho hàm số bậc ba $y = f(x)$ đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số $m$ thuộc đoạn $\lbrack - 10;10\rbrack$ để phương trình $2\left| f(x) \right| - m = 0$ có $2$ nghiệm phân biệt?

Tập hợp các giá trị của tham số $m$ để đồ thị hàm số $y = (x - 1)\left( x^{2} + mx + m \right)$ cắt trục hoành tại ba điểm phân biệt là

Tập hợp các giá trị thực của tham số $m$ để đồ thị hàm số $y = x^{3} - 3x^{2}$ cắt đường thẳng $y = m$ tại ba điểm phân biệt là

Cho phương trình $2x^{3} - 3x^{2} = 2m + 1.$ Giá trị thực của tham số $m$ để phương trình đã cho có đúng hai nghiệm phân biệt là

Giá trị của tham số $m$ để đồ thị hàm số $y = x^{3} - mx^{2} + 4$ cắt trục hoành tại ba điểm phân biệt là

Giá trị của tham số $m$ để đồ thị hàm số $y = x^{3} - 3mx^{2} + 2$ có đúng hai điểm chung với trục hoành là

Giá trị thực của tham số $m$ để phương trình $x^{3} - 3mx + 2 = 0$ có nghiệm duy nhất là

Giá trị của tham số $m$ để đường thẳng $d:y = m(x - 1) + 1$ cắt đồ thị hàm số $y = - x^{3} + 3x - 1$ tại ba điểm phân biệt $A(1;1),B,C$ là

Giá trị của tham số $m$ để đồ thị hàm số $y = x^{3} - 3x^{2} + 2$ cắt đường thẳng $d:y = m(x - 1)$ tại ba điểm phân biệt có hoành độ $x_{1},x_{2},x_{3}$ thỏa mãn $x_{1}^{2} + x_{2}^{2} + x_{3}^{2} = 5$ là

Giá trị của tham số $m$ để đường thẳng $d:y = x + 4$ cắt đồ thị hàm số $y = x^{3} + 2mx^{2} + (m + 3)x + 4$ $\left( C_{m} \right)$ tại ba điểm phân biệt $A(0;4),B,C$ sao cho tam giác $\text{MBC}$ có diện tích bằng $4$, với $M(1;3)$ là

Tập hợp các giá trị thực của tham số $m$ để đường thẳng $d:y = - \ mx$ cắt đồ thị của hàm số $y = x^{3} - 3x^{2} - m + 2$ $(C)$ tại ba điểm phân biệt $A,B,C$ sao cho $AB = BC$ là

Giá trị của tham số $m$ để đồ thị hàm số $y = x^{3} - 3mx^{2} + 6mx - 8$ cắt trục hoành tại ba điểm phân biệt có hoành độ lập thành cấp số cộng là

lý thuyết

Biện luận số nghiệm của phương trình ${a}{x}^{{4}}{+ b}{x}^{{2}}{+ c = m}\left( {a >}{0,}{b <}{0} \right){.}$ $\left( {1} \right)$

Cách 1. Phương trình $ax^{4} + bx^{2} + c = m$ là phương trình hoành độ giao điểm của đồ thị hàm trùng phương $y = ax^{4} + bx^{2} + c$ và đường thẳng $y = m$ (có phương song song với trục hoành)

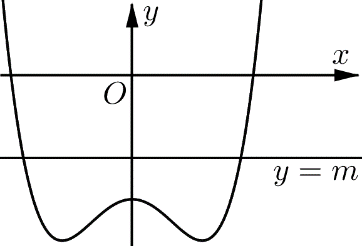
Do hệ số $a > 0,b < 0$ nên đồ thị hàm số $y = ax^{4} + bx^{2} + c$ có dạng như sau:

Dựa vào đồ thị ta có: $\bullet$ $(1)$ vô nghiệm $\Leftrightarrow m < y_{\text{CT}}.$ $\bullet$ $(1)$ có $2$ nghiệm $\Leftrightarrow \left\lbrack \begin{aligned}m = y_{\text{CT}} \\m > y_{\text{CD}} \\\end{aligned} \right.\ .$ $\bullet$ $(1)$ có $3$ nghiệm $\Leftrightarrow m = y_{\text{CD}}.$ $\bullet$ $(1)$ có $4$ nghiệm $\Leftrightarrow y_{\text{CT}} < m < y_{\text{CD}}.$

Cách 2. Phương trình $ax^{4} + bx^{2} + c = m\overset{}{\leftrightarrow}ax^{4} + bx^{2} + c - m = 0.$ $\left( {2} \right)$

Do hệ số $a > 0,b < 0$ nên đồ thị hàm số $y = ax^{4} + bx^{2} + c - m$ có dạng như sau:

Ta có các trường hợp sau: $\bullet$ $(2)$ vô nghiệm $\Leftrightarrow y_{\text{CT}} > 0.$ $\bullet$ $(2)$ có $2$ nghiệm $\Leftrightarrow \left\lbrack \begin{aligned}y_{\text{CT}} = 0 \\y_{\text{CD}} < 0 \\\end{aligned} \right.\ .$ $\bullet$ $(2)$ có $3$ nghiệm $\Leftrightarrow y_{\text{CD}} = 0.$ $\bullet$ $(2)$ có $4$ nghiệm $\Leftrightarrow y_{\text{CT}} < 0 < y_{\text{CD}}.$

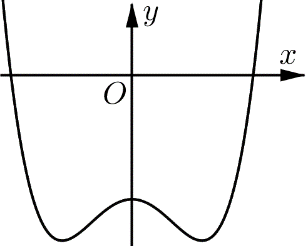Với điều kiện nào của tham số $k$ thì phương trình $4x^{2}\left( 1 - x^{2} \right) = 1 - k$ có bốn nghiệm phân biệt?

Cho hàm số $y = x^{4} - m(m + 1)x^{2} + m^{3}$ với $m$ là tham số thực. Tìm tất cả các giá trị của $m$ để đồ thị hàm số cắt trục hoành tại bốn điểm phân biệt.

Giá trị thực của tham số $m$ để phương trình $x^{4} - 2x^{2} + 2020 - m = 0$ có đúng ba nghiệm là

Cho hàm số $y = - x^{4} + 2(2 + m)x^{2} - 4 - m$ với $m$ là tham số thực. Có bao nhiêu giá trị nguyên của $m$ để đồ thị hàm số không có điểm chung với trục hoành?

Giá trị của tham số $m$ để đường thẳng $d:y = 2mx + m + 1$ cắt đồ thị hàm số $y = \dfrac{2x - 2}{2x + 1}$ $(C)$ tại hai điểm phân biệt là

Giá trị của tham số $m$ để đường thẳng $d:y = x - 2m$ cắt đồ thị hàm số $y = \dfrac{x - 3}{x + 1}$ $(C)$ tại hai điểm phân biệt có hoành độ dương là

Gọi $d$ là đường thẳng đi qua $A(1;0)$ và có hệ số góc $m.$ Giá trị của tham số $m$ để $d$ cắt đồ thị hàm số $y = \dfrac{x + 2}{x - 1}$ $(C)$ tại hai điểm phân biệt thuộc hai nhánh của đồ thị là

Tìm tất cả các giá trị thực của tham số $m$ để đường thẳng $d:y = - x + m$ cắt đồ thị hàm số $y = \dfrac{- 2x + 1}{x + 1}$ $(C)$ tại hai điểm $A,$ $B$ sao cho $AB = 2\sqrt{2}.$

Giá trị của tham số $m$ để đường thẳng $d:y = x - m + 2$ cắt đồ thị hàm số $y = \dfrac{2x}{x - 1}$ $(C)$ tại hai điểm phân biệt $A$ và $B$ sao cho độ dài $\text{AB}$ ngắn nhất là

Giá trị của tham số $k$ sao cho đường thẳng $d:y = x + 2k + 1$ cắt đồ thị hàm số $y = \dfrac{2x + 1}{x + 1}$ $(C)$ tại hai điểm phân biệt $A$ và $B$ sao cho các khoảng cách từ $A$ và $B$ đến trục hoành là bằng nhau là

Giá trị của tham số $m$ để đường thẳng $d:y = x + m$ cắt đồ thị hàm số $y = \dfrac{2x - 1}{x - 1}$ $(C)$ tại hai điểm phân biệt $A,\text{\ B}$ sao cho tam giác $\text{OAB}$ vuông tại $O,$ với $O$ là gốc tọa độ.

Giá trị của tham số $m$ để đường thẳng $d:\ y\ = \ - 3x\ + \ m$ cắt đồ thị hàm số $y\ = \ \dfrac{2x\ + \ 1}{x\ - \ 1}$ $(C)$ tại hai điểm phân biệt $A$ và $B$ sao cho trọng tâm tam giác $\text{OAB}$ thuộc đường thẳng $\text{Δ\ }:\ x\ - \ 2y\ - \ 2\ = \ 0,$ với $O$ là gốc tọa độ là

Giá trị của tham số $m$ để đường thẳng $d:y = 2x + m$ cắt đồ thị hàm số $y = \dfrac{2x - 4}{x - 1}$ $(C)$ tại hai điểm phân biệt $A$ và $B$ sao cho $4S_{\text{ΔIAB}} = 15,$ với $I$ là giao điểm của hai đường tiệm cận của đồ thị là