Phần tự luận (8 điểm) SVIP

Hướng dẫn giải:

Phân tích đa thức sau thành nhân tử:

a) $2x(x-3y) - 25(3y-x)$

$=2x(x-3y) + 25(x-3y)$

$=(2x + 25)(x-3y)$

b) $36x^2 - 24x + 4$;

$= (6x)^2 - 2.6x.2 + 2^2$

$= (6x-2)^2$

c) $(3x+2)^2 + 2 . (3x+2) . (3x-1) + (3x-1)^2$.

$= (3x+2+3x-1)^2$

$= (6x+1)^2$

Hướng dẫn giải:

a) Điều kiện: $x \neq 0, x \neq-5$.

b) $A = \dfrac{x^2+2 x}{2 x+10}+\dfrac{x-5}{x}-\dfrac{5 x-50}{2 x(x+5)}$

$= \dfrac{x^2+2 x}{2 x+10}+\dfrac{x-5}{x}+\dfrac{50-5 x}{2 x(x+5)}$

$=\dfrac{x^3+2 x^2+2 x^2-50+50-5 x}{2 x(x+5)}$

$=\dfrac{x\left(x^2+2 x+2 x-5\right)}{2 x(x+5)}$

$=\dfrac{x^2-x+5 x-5}{2(x+5)}$

$=\dfrac{(x-1)(x+5)}{2(x+5)}=\dfrac{x-1}{2}$

Nếu giá trị của biểu thức bằng $1$ thì giá trị của $\dfrac{x-1}{2}$ cũng bằng $1$. Ta có : $\dfrac{x-1}{2}=1$ khi $x-1=2$ hay $x=3$. 

Vì $x=3$ thoả mãn điều kiện nên đó là giá trị phải tìm.

c) Tương tự $\dfrac{x-1}{2}=-\dfrac{1}{2}$ khi $x-1=-1$ hay $x=0$ (không thoả mãn điều kiện). Vậy không có giá trị nào của $x$ để phân thức có giá trị bằng $-\dfrac{1}{2}$.

d) Tương tự $\dfrac{x-1}{2}=-3$ khi $x-1=-6$ hay $x=-5$ (không thoả mãn điểu kiện). Vậy không có giá trị nào của $x$ để phân thức có giá trị bằng $-3.$

Hướng dẫn giải:

Gọi phương trình đường thẳng $A B$ là $y=a x+b$ $(a,b \in \mathbb R $ và $a \neq 0)$.

Ta có $A(-3 ; 0) \in A B$ suy ra $0=a . (-3)+b$ hay $b=3 a$.

$B(0 ; 2) \in A B$ suy ra $2=a . 0+b$ hay $b=2$. Từ đó suy ra $a=\dfrac{2}{3}$.

Vậy phương trình đường thẳng $AB$ là $y=\dfrac{2}{3} x+2$.

Hướng dẫn giải:

1) Diện đáy của hình chóp tứ giác đều là

$6\,250 . 3 : 30 = 625$ (cm$^2$)

Độ dài cạnh đáy của hình chóp tứ giác đều là

$\sqrt{625} = 25$ (cm)

2) 

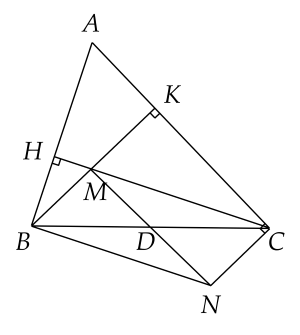
a) Xét tứ giác $BMCN$ có hai đường chéo $MN$ và $BC$ cắt nhau tại trung điểm mỗi đường, đo đó $BMNC$ là hình bình hành.

b) Vì $BMCN$ là hình bình hành nên ta suy ra $BM // NC$. Vậy $BKCN$ là hình thang. Mặt khác do $\widehat{BKC} = 90^{\circ}$ nên $BMCN$ là hình thang cân.

c) Để $BMCN$ là hình thoi thì $MD \perp BC$.

Mặt khác ta cũng có $AM \perp BC$ (giao điểm ba đường cao).

Kẻ đường thẳng $d$ vuông góc với $BC$, từ đây ta suy ra

$MD // d$ và $AM // d$. Vậy theo tiên đề Euclid, ta có 3 điểm $M,A,D$ thẳng hàng, hay $AD$ vừa là đường cao và vừa là đường trung tuyến của tam giác $ABC$.

Dễ dàng chứng minh được $\Delta AMD = \Delta ADC$, từ đó suy ra $AB = AC$, hay tam giác $ABC$ cân tại $A$.

Vậy để $BMCN$ là hình thoi thì $\Delta ABC $ là tam giác cân.

Hướng dẫn giải:

Biến đổi phương trình trở thành:

$\left({a}^2+{ab}+{b}^2-3\right)^2+3({a}-{b})^2=0$

$a^2+a b+b^2=3$ và $(a-b)^2=0$

$a^2+a b+b^2=3$ và $a=b$.

Thay $a=b$ vào $a^2+a b+b^2=3$, ta được:

$a^2+a.a+a^2=3$

$a^2=1$

Hay $a=b=1$ hoặc $a=b=-1$.

Vậy ta tìm được hai cặp $(a;b)$ là $(1;1)$ và $(-1;-1)$.