Phần tự luận (8 điểm) SVIP

Hướng dẫn giải:

a) $5(x+2y)-15x(x+2y)=5(x+2y).(1-3x)$.

b) $4{{x}^{2}}-12x+9=\left[ {{(2x)}^{2}}-2.2x.3+{{3}^{2}} \right]={{(2x-3)}^{2}}$.

c) ${{(3x-2)}^{3}}-3(x-4)(x+4)+{{(x-3)}^{3}}-(x+1)\left( {{x}^{2}}-x+1 \right)$

$=27{{x}^{3}}-54{{x}^{2}}+36x-8-3\left( {{x}^{2}}-16 \right)+{{x}^{3}}-9{{x}^{2}}+27x-27-\left( {{x}^{3}}+1 \right)$

$=\left( 27{{x}^{3}}+{{x}^{3}}-{{x}^{3}} \right)+\left( -54{{x}^{2}}-3{{x}^{2}}-9{{x}^{2}} \right)+(36x+27x)+(-8+48-27-1)$

$=27{{x}^{3}}-66{{x}^{2}}+63x+12$.

Hướng dẫn giải:

a) Thay $x=2$ (thỏa mãn điều kiện xác định) vào $Q=\dfrac{x+1}{{{x}^{2}}-9}$, ta được:

$Q=\dfrac{x+1}{{{x}^{2}}-9}=\dfrac{2+1}{{{2}^{2}}-9}=\dfrac{3}{-5}=-\dfrac{3}{5}$.

b) $P=\dfrac{2{{x}^{2}}-1}{x(x+1)}-\dfrac{(x-1)(x+1)}{x(x+1)}+\dfrac{3x}{x(x+1)}$

$P=\dfrac{2{{x}^{2}}-1-\left( {{x}^{2}}-1 \right)+3x}{x(x+1)}$

$P=\dfrac{2{{x}^{2}}-1-{{x}^{2}}+1+3x}{x(x+1)}$

$P=\dfrac{{{x}^{2}}+3x}{x(x+1)}=\dfrac{x+3}{x+1}$.

c) Ta có $M=P.Q=\dfrac{x+3}{x+1}. \dfrac{x+1}{{{x}^{2}}-9}=\dfrac{x+3}{(x-3)(x+3)}=\dfrac{1}{x-3}$

$M=\dfrac{-1}{2}$ suy ra $\dfrac{1}{x-3}=\dfrac{-1}{2}$

$x-3=-2$

$x=1$.

Vậy với $x=1$ thì$M=\dfrac{-1}{2}$.

Hướng dẫn giải:

Vì đồ thị hàm số $y=ax+b$ đi qua điểm $A\left( -1;2 \right)$ nên ta có:

   $2=-1.a+b$ suy ra $-a+b=2$

Vi đồ thị hàm số $y=ax+b$ đi qua điểm $B\left( 1;4 \right)$ nên ta có:

   $4=1.a+b$ suy ra $a+b=4\left( 2 \right)$

Từ (1) và (2) ta tìm được $a=1;\,\,b=3$

Vậy hàm số cần tìm là $y=x+3$.

Hướng dẫn giải:

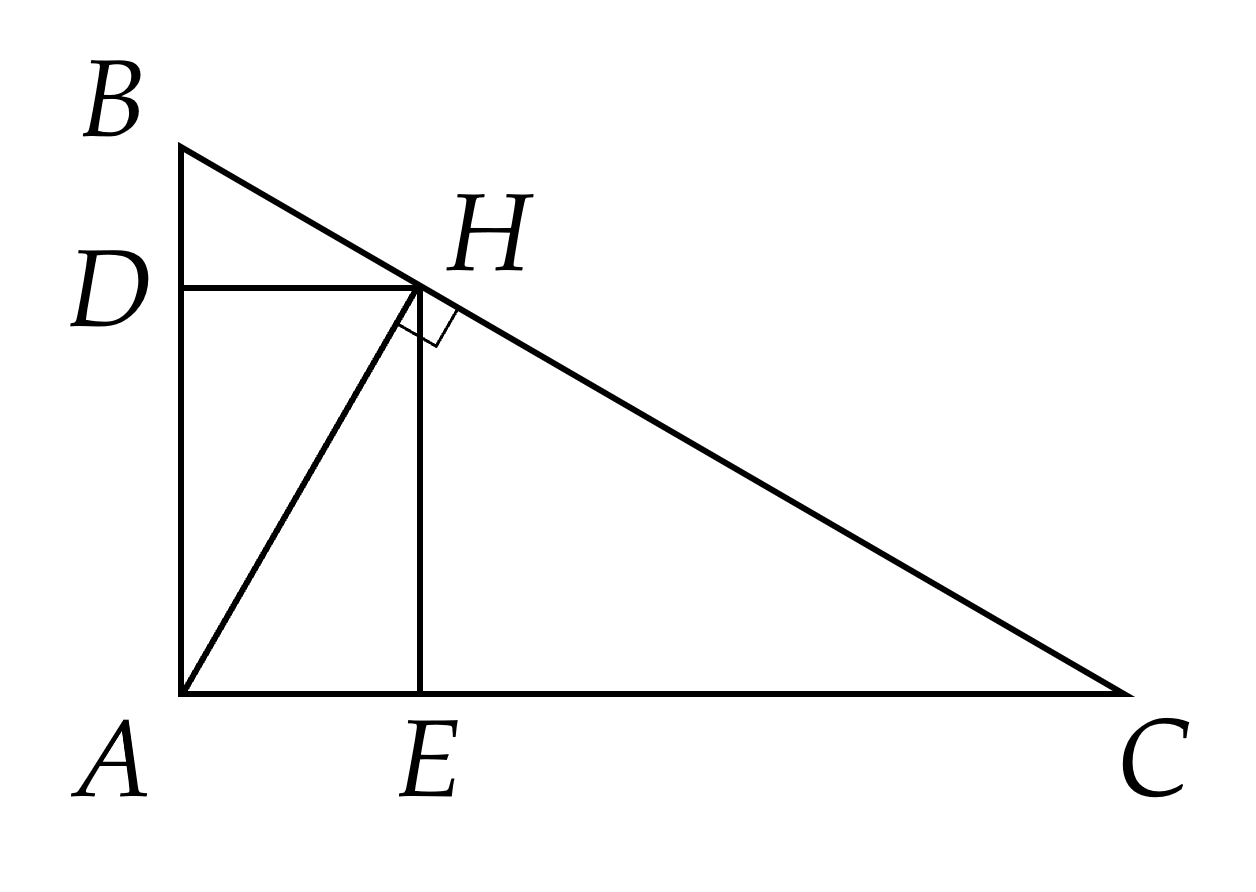
a) $\Delta ABC$ vuông tại $A$ suy ra $\widehat{BAC}=90^\circ$ suy ra $\widehat{DAE}=90^\circ$.

Do $HD\bot AB$ suy ra $\widehat{HDA}=90^\circ $; $HE\bot AC$ suy ra $\widehat{HEA}=90^\circ$.

Tứ giác $ADHE$ có $\widehat{DAE}=\widehat{HDA}=\widehat{HEA}=90^\circ$ suy ra tứ giác $ADHE$ là hình chữ nhật. 

b) Do $\Delta AHD$ vuông tại $D$, áp dụng định lí Pythagore suy ra:

$A{{H}^{2}}=A{{D}^{2}}+D{{H}^{2}}$

$25=16+D{{H}^{2}}$

$D{{H}^{2}}=9$ nên $DH=3$ cm.

Do $ADHE$ là hình chữ nhật suy ra ${{S}_{ADHE}}=AD.DH=4.3=12$ (cm$^2$).

Hướng dẫn giải:

Từ $x+y+z=0$ suy ra $x+y=-z$

${{x}^{2}}+2xy+{{y}^{2}}={{z}^{2}}$

${{x}^{2}}+{{y}^{2}}-{{z}^{2}}=-2xy$.

Tương tự ta có: ${{y}^{2}}+{{z}^{2}}-{{x}^{2}}=-2yz$ và ${{z}^{2}}+{{x}^{2}}-{{y}^{2}}=-2zx $.

Do đó $A=\dfrac{xy}{-2xy}+\dfrac{yz}{-2yz}+\dfrac{zx}{-2zx}=-\dfrac{1}{2}-\dfrac{1}{2}-\dfrac{1}{2}=-\dfrac{3}{2}$.

Vậy $A=-\dfrac{3}{2}$.