Hình chiếu vuông góc SVIP

1. Hình biểu diễn của một hình, khối.

$*)$ Nhắc lại khái niệm về phép chiếu mà em đã học:

​@201918466441@

2. Hình chiếu đứng, hình chiếu bằng và hình chiếu cạnh:

Cho hình $\mathscr{H}$ trong không gian và ba mặt phẳng $\left(P_1\right),\left(P_2\right),\left(P_3\right)$ đôi một vuông góc với nhau sao cho:

+) Mặt phẳng $\left(P_1\right)$ vuông góc với hướng nhìn từ phía trước của hình $\mathscr{H}$;

+) Mặt phẳng $\left(P_2\right)$ vuông góc với hướng nhìn từ phía trên của hình $\mathscr{H}$;

+) Mặt phẳng $\left(P_3\right)$ vuông góc với hướng nhìn từ phía trái của hình $\mathscr{H}$.

Khi đó:

+) Các mặt phẳng $\left(P_1\right),\left(P_2\right)$ và $\left(P_3\right)$ lần lượt được gọi là mặt phẳng hình chiếu đứng, mặt phẳng hình chiếu bằng và mặt phẳng hình chiếu cạnh.
+) Các hình chiếu vuông góc của hình $\mathscr{H}$ lên các mặt phẳng $\left(P_1\right),\left(P_2\right),\left(P_3\right)$ lần lượt được gọi là hình chiếu đứng, hình chiếu bằng và hình chiếu cạnh của hình $\mathscr{H}$.

3. Mối liên hệ giữa ba hình chiếu vuông góc:

$*)$ Từ hai hình chiếu vuông góc $A_1$ và $A_2$ của điểm $A$, ta sẽ xác định được vị trí của điểm $A$ trong không gian.

Mặt khác, từ hình vẽ ta thấy $A_1A_2$ vuông góc với $Ox$ (giao tuyến của hai mặt phẳng hình chiếu).​

Nếu ta mở rộng mặt phẳng $(P_2)$ sao cho trùng với $(P_1)$ thì ta thấy $A_1 A_2$ vuông góc với $Ox$.

$*)$ Trong không gian, một trong ba điểm $A_1, A_2,A_3$ hoàn toàn được xác định nếu biết hai điểm còn lại.

Trên hình vẽ, ta thấy $A_1AA_3P. M A_2 N O$ là hình lập phương, do đó ta thấy $A_2M=A_3P$.

Khi mở hai mặt phẳng $(P_2)$ và $(P_3)$ trùng với mặt phẳng $(P_1)$, ta có hình vẽ:

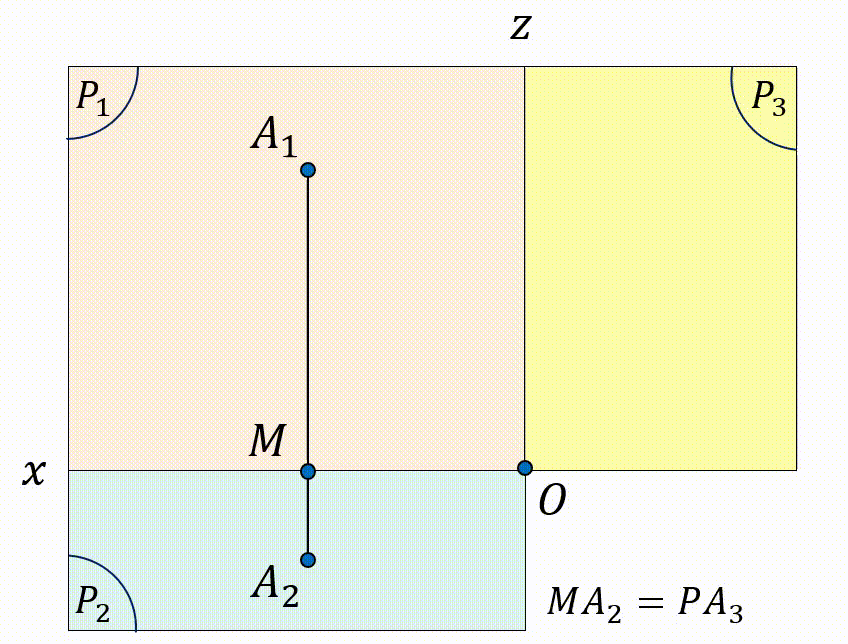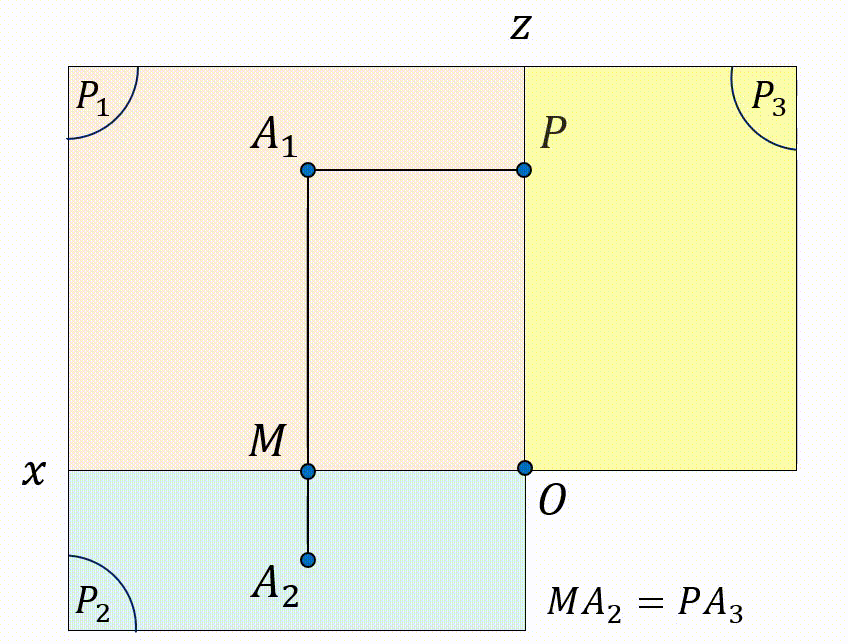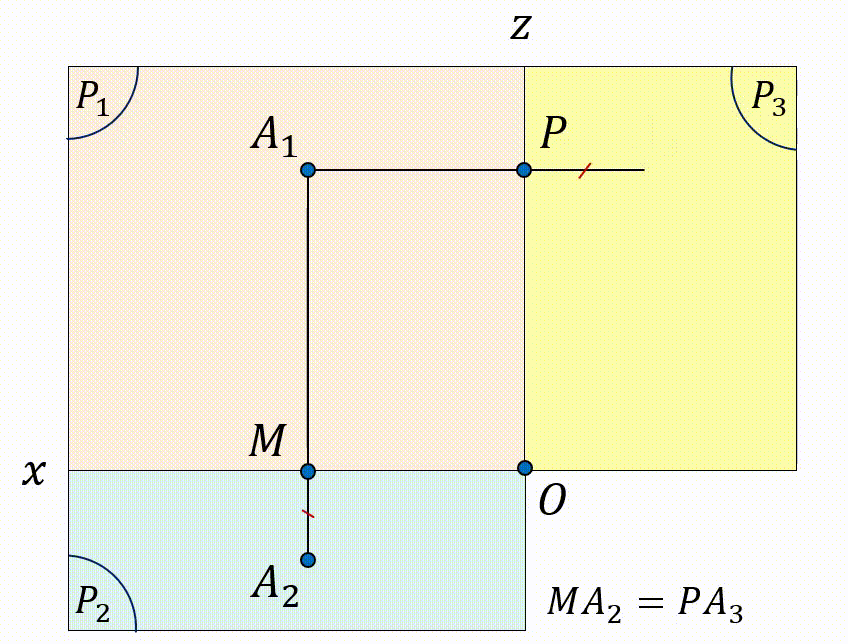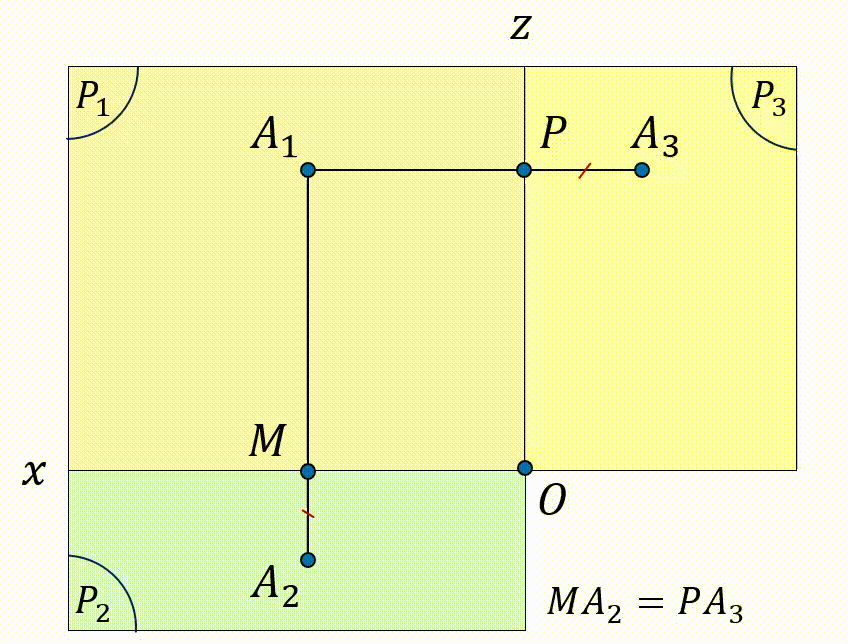
Vậy, khi biết vị trí 2 trong 3 hình chiếu của điểm $A$, ta hoàn toàn có thể xác định điểm còn lại. Mở rộng với hình $H$ bất kì, khi biết 2 hình chiếu của $H$, ta có thể vẽ được hình chiếu thứ 3 của hình $H$.

Ví dụ: Cho hình chiếu đứng và hình chiếu bằng của đoạn thẳng $AB$ trong không gian, hãy xác định hình chiếu cạnh của đoạn thẳng đó.

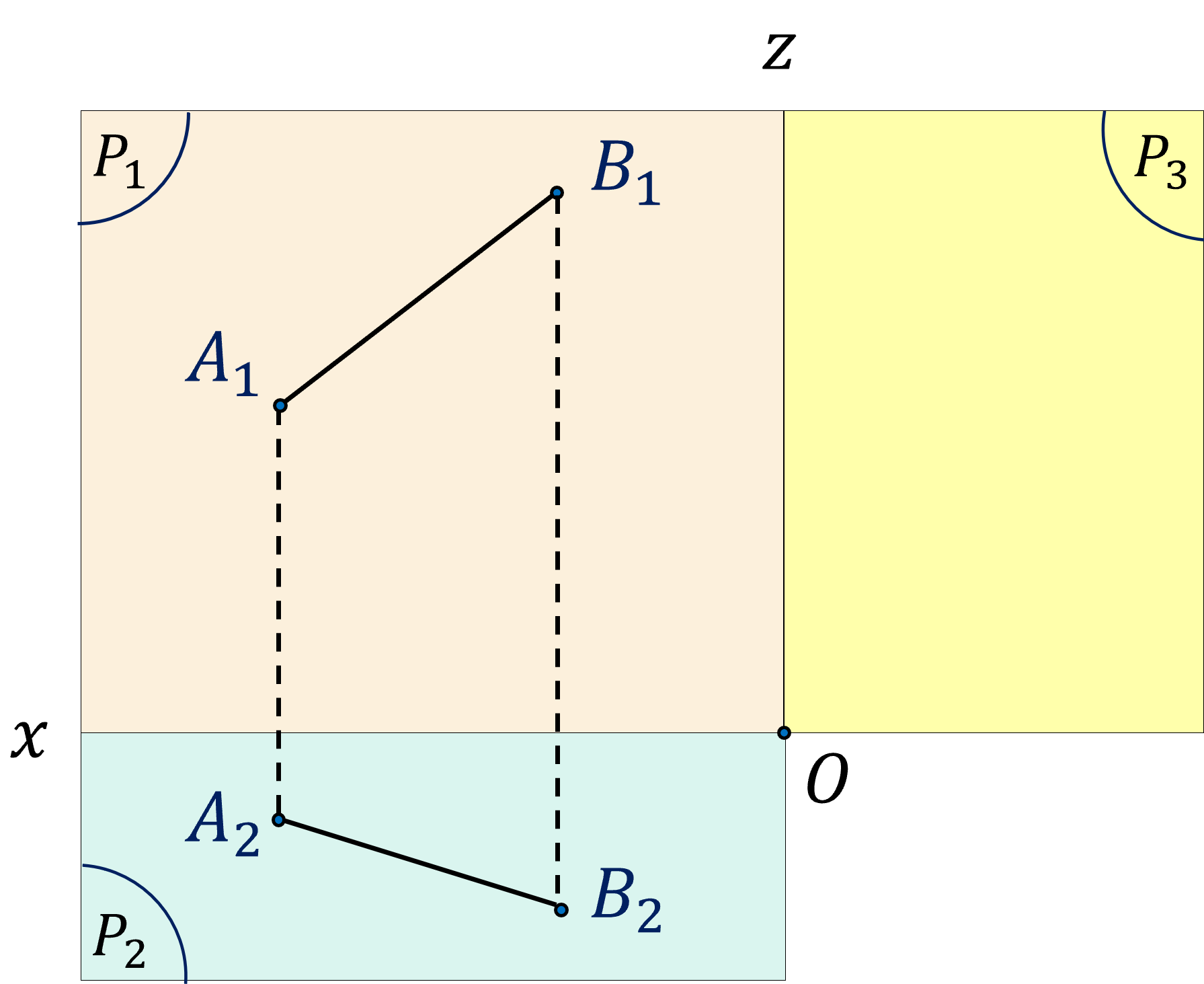
 Giải

Ta xác định từng hình chiếu của hai đầu mút. 

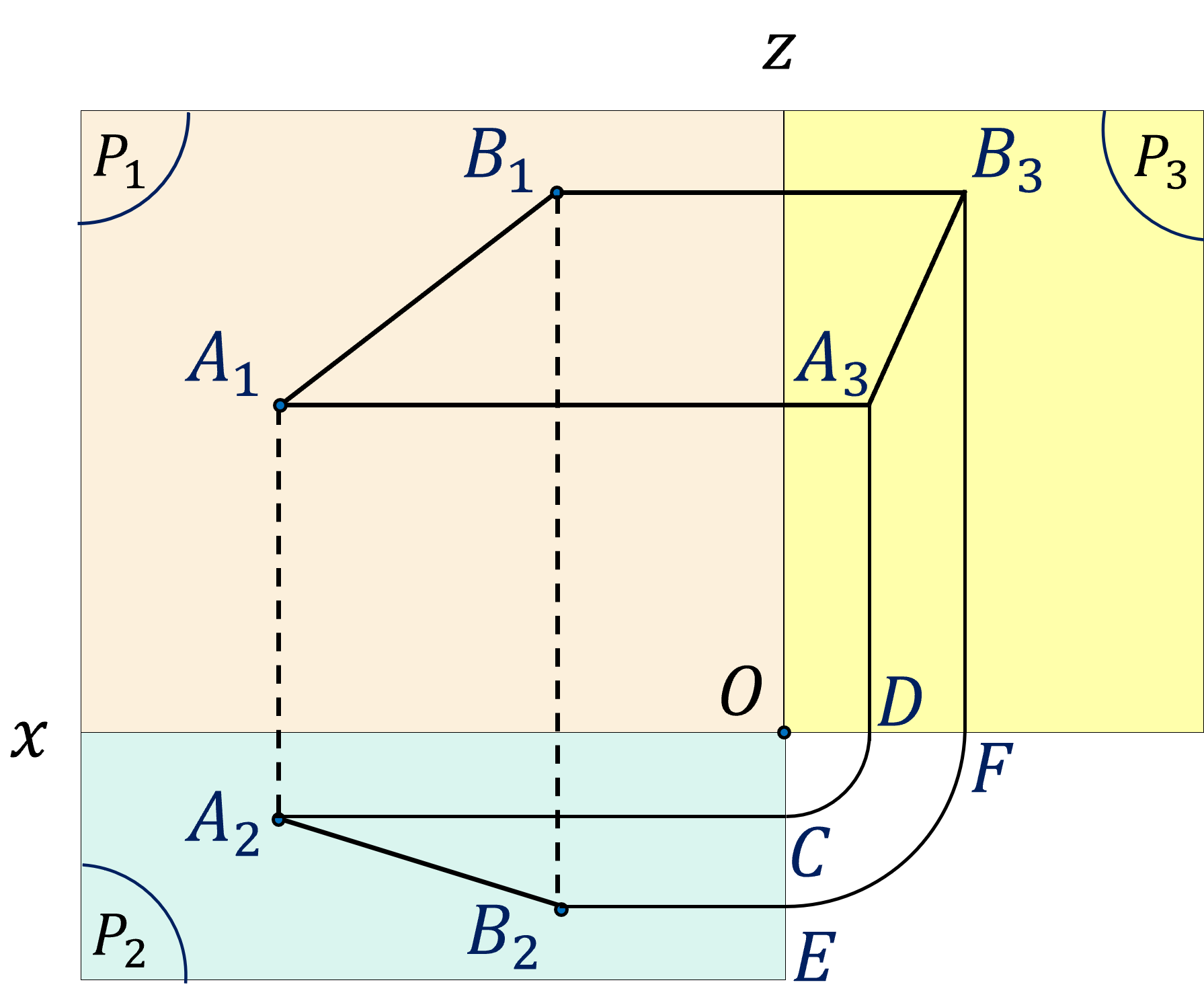
Hình chiếu cạnh của đoạn thẳng $A B$ có hai đầu mút là hình chiếu cạnh $A_3$ của $A$ và $B_3$ của $B$. Để xác định $A_3$ ta làm như sau: Qua điểm $A_2$ vẽ đường thẳng vuông góc với $O z$ tại $C$ và trên $O x$ lấy điểm $D$ sao cho $O C=O D$ (xem hình vẽ bên dưới). Đường thẳng qua $A_1$ và vuông góc với $O z$ cắt đường thẳng qua $D$ và vuông góc với $O x$ tại $A_3$. Tương tự xác định $B_3$. Nối $A_3$ và $B_3$ ta nhận được hình chiếu cạnh của đoạn thẳng $A B$.