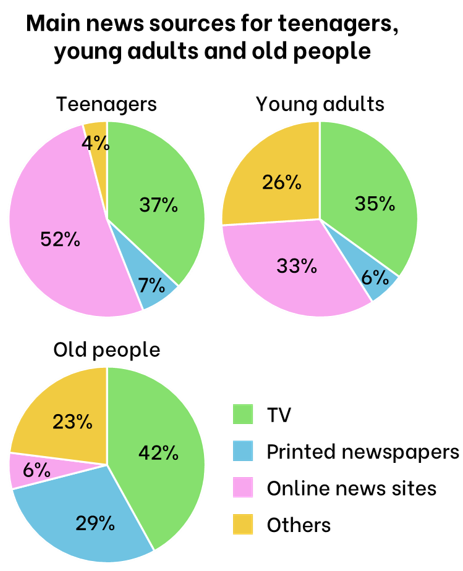
Write a description (120-150 words) of the charts below.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta có \(\sqrt{2+2\cos2x}=\sqrt{2+2\left(2\cos^2x-1\right)}=\sqrt{4\cos^2x}=2\left|\cos x\right|\)
\(\Leftrightarrow f\left(x\right)+f\left(-x\right)=2\left|\cos x\right|,\forall x\inℝ\) (1)
Đặt \(g\left(x\right)=f\left(x\right)-\left|\cos x\right|\)
Khi đó (1) \(\Leftrightarrow\left[f\left(x\right)-\left|\cos x\right|\right]+\left[f\left(-x\right)-\left|\cos x\right|\right]=0\)
\(\Leftrightarrow g\left(x\right)+\left[f\left(-x\right)-\left|\cos\left(-x\right)\right|\right]=0\) (do \(\cos x\) là hàm chẵn)
\(\Leftrightarrow g\left(x\right)+g\left(-x\right)=0\)
\(\Leftrightarrow g\left(x\right)=-g\left(-x\right)\)
\(\Leftrightarrow g\left(x\right)\) là hàm lẻ
Khi đó \(f\left(x\right)=g\left(x\right)+\left|\cos x\right|\) với \(g\left(x\right)\) là hàm lẻ. Thử lại, ta thấy:
(1) \(\Leftrightarrow f\left(x\right)+f\left(-x\right)=g\left(x\right)+\left|\cos x\right|+g\left(-x\right)+\left|\cos\left(-x\right)\right|\)
\(\Leftrightarrow f\left(x\right)+f\left(-x\right)=2\left|\cos x\right|\), thỏa mãn
Vậy \(f\left(x\right)=g\left(x\right)+\left|\cos x\right|\) với \(g\left(x\right)\) là hàm lẻ bất kì có tập xác định là \(ℝ\)
\(\Rightarrow I=\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}f\left(x\right)dx\)
\(I=\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}\left[g\left(x\right)+\left|\cos x\right|\right]dx\)
\(I=\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}g\left(x\right)dx+\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}\left|\cos x\right|dx\)
\(I=\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}\left|\cos x\right|dx\) (do \(g\left(x\right)\) là hàm lẻ)
\(I=\int\limits^{-\dfrac{\pi}{2}}_{-\dfrac{3\pi}{2}}\left(-\cos x\right)dx+\int\limits^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}\cos xdx+\int\limits^{\dfrac{3\pi}{2}}_{\dfrac{\pi}{2}}\left(-\cos x\right)dx\)
\(I=-\sin x|^{-\dfrac{\pi}{2}}_{-\dfrac{3\pi}{2}}+\sin x|^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}-\sin x|^{\dfrac{3\pi}{2}}_{\dfrac{\pi}{2}}\)
\(I=6\)

\(x=3y\) và y = 5\(x\) thay y = 5\(x\) vào \(x\) = 3y ta có: \(x\) = 3.5\(x\)
⇒ \(x\) = 15\(x\) ⇒ \(x-15x\) = 0 ⇒ \(-14\)\(x\) = 0 ⇒ \(x=0\)
Thay \(x\) = 0 vào y = 5\(x\) ta được: y= 5.0 = 0
Vậy \(x=3\)y; y = 5\(x\) thì y = 0

em chỉ thử làm thôi ạ:
Tương tự như thế vậy xuống 100m thì tăng 0,6 độ C và xuống 1000m thì tăng 6 độ C
Khi viết về biểu đồ tròn trong IELTS Writing Task 1, bạn cần tuân theo một cấu trúc rõ ràng để phân tích một cách đầy đủ và mạch lạc:
1. Mở bài:
Giới thiệu ngắn gọn nội dung của biểu đồ bằng cách diễn đạt lại đề bài. Ví dụ: "Biểu đồ tròn minh họa sự phân bổ các nguồn năng lượng được sản xuất tại Pháp vào các năm 1995 và 2005."
2. Tổng quan:
Khái quát những xu hướng chính mà bạn quan sát được. Ví dụ: "Có thể thấy rằng tỷ lệ năng lượng được tạo ra từ xăng dầu giảm đi, trong khi tỷ lệ từ than và khí đốt lại tăng nhẹ."
3. Thân bài:
Phân tích chi tiết sự khác biệt, có thể dựa theo từng năm hoặc theo từng loại năng lượng. Ví dụ:
"Năm 1995, than chiếm tỷ lệ cao nhất trong sản xuất năng lượng, với 29,8%, trong khi xăng dầu chiếm 29,3%. Đến năm 2005, tỷ lệ từ than tăng lên 30,9%, trong khi xăng dầu giảm đáng kể, chỉ còn khoảng 20%."
4. Kết luận:
Đánh giá xu hướng chung dựa trên dữ liệu, nhưng không giới thiệu dữ liệu mới. Ví dụ: "Nhìn chung, trong khi tỷ lệ từ than và khí đốt tăng, sự phụ thuộc vào xăng dầu đã giảm đi đáng kể trong vòng một thập kỷ."
Việc sử dụng các so sánh rõ ràng và các con số chính xác sẽ giúp bài viết của bạn chặt chẽ hơn và đạt được kỳ vọng khi phân tích biểu đồ tròn trong bài thi IELTS.