Trong nhà thì Lan là con thứ 2. Mẹ hơn Lan 30 tuổi. 5 năm sau Lan bằng 1/4 tuổi mẹ. Tính số tuổi mỗi người.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Số ngày còn lại theo dự định 60 người phải làm:
36 - 16 = 20 (ngày)
Số ngày thực tế làm:
20 + 10 = 30 (ngày)
Do cùng làm một đoạn đường và xem sức làm việc của mỗi người là như nhau nên số người và số ngày là hai đại lượng tỉ lệ nghịch
Số người còn lại làm hoàn thành đoạn đường trong 30 ngày:
60 × 20 : 30 = 40 (người)

Phương trình hoành độ giao điểm của (d') và (d):
2x + m - 1 = x - 3
⇔ 2x - x + m = -3 + 1
⇔ x + m = -2 (1)
(d') cắt (d) tại một điểm trên trục tung nên thay x = 0 vào (1), ta có:
0 + m = -2
⇔ m = -2
Vậy m = -2 thì (d') cắt (d) tại một điểm trên trục tung

Bài 1
∆' = (-4)² - (m - 1)
= 16 - m + 1
= 17 - m
Để phương trình có hai nghiệm phân biệt thì ∆' > 0
⇔ 17 - m > 0
⇔ m < 17
Theo hệ thức Vi-ét, ta có:
x₁ + x₂ = 8
x₁x₂ = m - 1
P = (x₁² - 1)(x₂² - 1) + 2087
= (x₁x₂)² - x₁² - x₂² + 1 + 2087
= (x₁x₂)² - (x₁² + x₂²) + 2088
= (x₁x₂)² - [(x₁ + x₂)² - 2x₁x₂] + 2088
= (x₁x₂)² - (x₁ + x₂)² + 2x₁x₂ + 2088
= (m - 1)² - 8² + 2(m - 1) + 2088
= (m - 1)² + 2(m - 1) + 1 - 1 - 64 + 2088
= (m - 1 + 1)² + 2023
= m² + 2023 ≥ 2023 với mọi m ∈ R
Vậy GTNN của P là 2023 khi m = 0

a: \(-3x^2+5x+1=0\)
=>\(3x^2-5x-1=0\)
\(\text{Δ}=\left(-5\right)^2-4\cdot3\cdot\left(-1\right)=25+12=37>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{5-\sqrt{37}}{2\cdot3}=\dfrac{5-\sqrt{37}}{6}\\x_2=\dfrac{5+\sqrt{37}}{6}\end{matrix}\right.\)

Câu 8:
a) Ta có:
- Góc BFC và góc BEC cùng nhìn cạnh BC dưới hai góc vuông (do BF và BE là đường cao), suy ra tứ giác BFEC nội tiếp.
Tứ giác CDHE nội tiếp vì:
- Góc CHD và góc CED cùng nhìn cạnh CD dưới hai góc vuông (do CF và DE là đường cao), suy ra tứ giác CDHE nội tiếp.
b) Theo định lý Pascal, ta có:
- Giao điểm của AH và BE là H.
- Giao điểm của HG và EK là I (do HI//DE và DE cắt EK tại I).
- Giao điểm của GB và KA là J (do HJ//DF và DF cắt KA tại J).
Vì H, I, J thẳng hàng, theo định lý Pascal, điểm K cũng phải nằm trên đường thẳng này, suy ra I, J, K thẳng hàng.
c) Ta có:
- CF là tiếp tuyến của (O) tại C (do CF là đường cao và F là tiếp điểm).
- CL là dây cung (do L nằm trên (O)).
Vì góc CFL là góc tạo bởi tiếp tuyến CF và dây cung CL, nên góc CFL bằng góc LCO (góc nội tiếp cùng chắn cung CL). Tương tự, góc LFC bằng góc LCO. Do đó, C, F, L thẳng hàng.
Ta có:
- Góc ANG bằng góc AGH (do HI//DE và HJ//DF).
- Góc AGH bằng nửa góc AOH (góc ở tâm cùng chắn cung AH).
Vì AH là đường kính của (O), nên góc AOH là góc vuông. Do đó, góc AGH là \(\dfrac{1}{2}\) góc vuông, suy ra tam giác AHG vuông tại H. Áp dụng định lý Pythagoras cho tam giác AHG, ta có:
\(AN\cdot AG=AH^2\)

Lời giải:
Áp dụng định lý Viet:
$x_1+x_2=4$
$x_1x_2=2$
Ta có:
$P=\frac{1}{x_1^2}-\frac{1}{x_2^2}+2024$
$=\frac{x_2^2-x_1^2}{(x_1x_2)^2}+2024$
$=\frac{(x_2-x_1)(x_2+x_1)}{(x_1x_2)^2}+2024$
$=\frac{4(x_2-x_1)}{2^2}+2024$
$=x_2-x_1+2024$
Vì $x_1>x_2$ nên $x_2-x_1<0$. Do đó:
$x_2-x_1=-|x_1-x_2|=-\sqrt{(x_1-x_2)^2}=-\sqrt{(x_1+x_2)^2-4x_1x_2}$
$=-\sqrt{4^2-4.2}=-2\sqrt{2}$
Do đó: $P=-2\sqrt{2}+2024$

Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=4\\x_1x_2=\dfrac{c}{a}=2\end{matrix}\right.\)
\(x_1>x_2\)
=>\(x_1-x_2>0\)
\(\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1x_2\)
\(=4^2-4\cdot2=8\)
=>\(x_1-x_2=2\sqrt{2}\)(do x1-x2>0)
\(P=\dfrac{1}{x_1^2}-\dfrac{1}{x_2^2}+2024\)
\(=\dfrac{x_2^2-x_1^2}{\left(x_1x_2\right)^4}+2024\)
\(=\dfrac{\left(x_2-x_1\right)\left(x_2+x_1\right)}{2^4}+2024\)
\(=\dfrac{\left(x_2-x_1\right)\cdot4}{16}+2024=\dfrac{\left(x_2-x_1\right)}{4}+2024\)
\(=\dfrac{-2\sqrt{2}}{4}+2024=-\dfrac{\sqrt{2}}{2}+2024=\dfrac{4048-\sqrt{2}}{2}\)

Lời giải:
Áp dụng định lý Viet:
$x_1+x_2=4$
$x_1x_2=2$
Khi đó:
$P=\frac{1}{x_1^2}+\frac{1}{x_2^2}+2024$
$=\frac{x_1^2+x_2^2}{x_1^2x_2^2}+2024$
$=\frac{(x_1+x_2)^2-2x_1x_2}{(x_1x_2)^2}+2024$
$=\frac{4^2-2.2}{2^2}+2024=2027$

Lời giải:
Với $n$ nguyên, để $\frac{3n+2}{4n-5}$ là số nguyên thì:
$3n+2\vdots 4n-5$
$\Rightarrow 4(3n+2)\vdots 4n-5$
$\Rightarrow 12n+8\vdots 4n-5$
$\Rightarrow 3(4n-5)+23\vdots 4n-5$
$\Rightarrow 23\vdots 4n-5$
Với $n$ nguyên $\Rightarrow 4n-5\in Ư(23)$
$\Rightarrow 4n-5\in \left\{-1; -23; 1; 23\right\}$
$\Rightarrow n\in \left\{1; -4,5; 1,5; 7\right\}$
Vì $n$ nguyên nên $n\in\left\{1; 7\right\}$




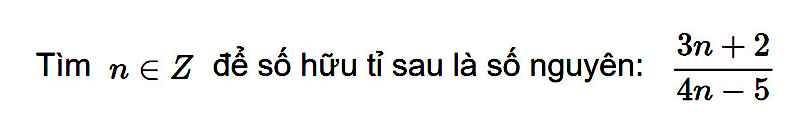
5 năm sau, tuổi mẹ vẫn hơn tuổi Lan 30 tuổi
Hiệu số phần bằng nhau:
4 - 1 = 3 (phần)
Tuổi mẹ hiện nay:
30 : 3 × 4 - 5 = 35 (tuổi)
Tuổi con hiện nay:
35 - 30 = 5 (tuổi)
Tính số tuổi mỗi người hiện nay hay tuổi mỗi người 5 năm sau em nhỉ?