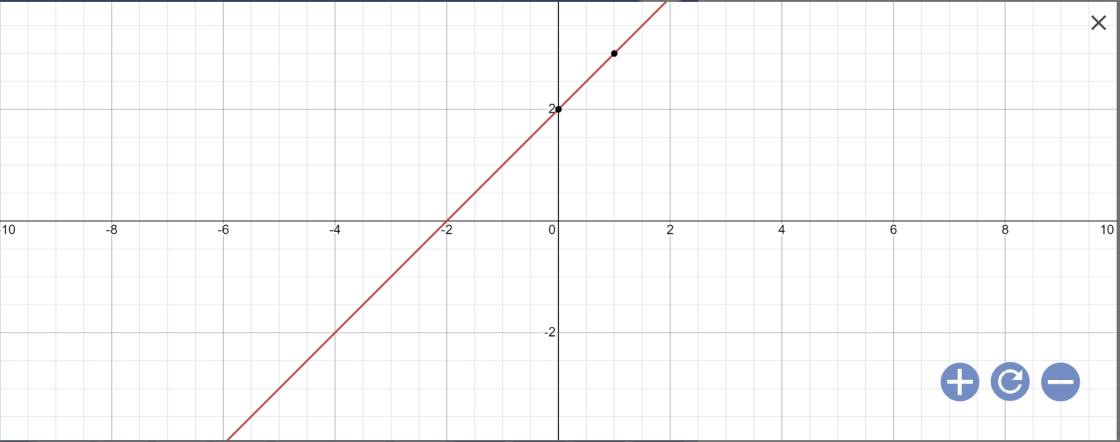
Giúp mình với ạ gi
gi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta giả sử 36 con đều là gà thì tổng số chân gà là:
2 x 36 = 72 (chân)
Như vậy số chân còn thiếu là:
100 - 72 = 28 (chân)
Mỗi con chó hơn mỗi con gà số chân là:
4 - 2 = 2 (chân)
Số con chó là:
28 : 2 = 14 (con)
Số con gà là:
36 - 14 = 22 (con)
Đáp số: 14 con chó và 22 con gà.
giả sử 36 con là con chó=> số chân là:36x4=144(cái chân)
sở dĩ ta bị thừa 44 cái chân do ta coi tất cả là chó
số gà là:44:=22(con)
số chó là:36-22=14(con)
easy

Bài 2:
a: \(x^2\left(x-2\right)+2-x=0\)
=>\(x^2\left(x-2\right)-\left(x-2\right)=0\)
=>\(\left(x-2\right)\left(x^2-1\right)=0\)
=>(x-2)(x+1)(x-1)=0
=>\(\left[{}\begin{matrix}x-2=0\\x+1=0\\x-1=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=2\\x=-1\\x=1\end{matrix}\right.\)
b: \(x^2-9x^3=x^2-9x\)
=>\(9x^3=9x\)
=>\(x^3=x\)
=>\(x^3-x=0\)
=>\(x\cdot\left(x^2-1\right)=0\)
=>x(x-1)(x+1)=0
=>\(\left[{}\begin{matrix}x=0\\x-1=0\\x+1=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=0\\x=1\\x=-1\end{matrix}\right.\)
c: \(x\left(x+2\right)+x^2=-2x\)
=>\(x\left(x+2\right)+x^2+2x=0\)
=>2x(x+2)=0
=>x(x+2)=0
=>\(\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
d: \(\left(x+1\right)\left(x^2+4\right)=x^2+x\)
=>\(\left(x+1\right)\left(x^2+4\right)-x\left(x+1\right)=0\)
=>\(\left(x+1\right)\left(x^2-x+4\right)=0\)
mà \(x^2-x+4=\left(x-\dfrac{1}{2}\right)^2+\dfrac{15}{4}>=\dfrac{15}{4}\forall x\)
nên x+1=0
=>x=-1

10 con chó có số cái chân là:
4x10=40(cái chân)
Đáp số : 40 cái chân
Số cái chân 10 con chó có là:
10 x 4 = 40 (cái chân)
Đáp số: 40 cái chân.
#hoctot

Câu 3:
a: Xét ΔBEF vuông tại E và ΔBAC vuông tại A có
\(\widehat{EBF}\) chung
Do đó: ΔBEF~ΔBAC
b: Xét ΔEDC vuông tại D và ΔEBF vuông tại E có
\(\widehat{EDC}=\widehat{EBF}\left(=90^0-\widehat{ACB}\right)\)
Do đó: ΔEDC~ΔEBF
=>\(\dfrac{ED}{EB}=\dfrac{EC}{EF}\)
=>\(ED\cdot EF=EB\cdot EC\)
Câu 1:
a:
\(A=\dfrac{x^2-9}{x-3}=\dfrac{\left(x-3\right)\left(x+3\right)}{x-3}=x+3\)
Thay x=4 vào A, ta được:
A=4+3=7
Thay x=4 vào B, ta được:
\(B=\dfrac{3}{4-3}+\dfrac{2}{4+3}+\dfrac{4^2-5\cdot4-3}{4^2-9}\)
\(=3+\dfrac{2}{7}+\dfrac{-7}{7}=3+\dfrac{2}{7}-1=2+\dfrac{2}{7}=\dfrac{16}{7}\)
b: \(B=\dfrac{3}{x-3}+\dfrac{2}{x+3}+\dfrac{x^2-5x-3}{x^2-9}\)
\(=\dfrac{3}{x-3}+\dfrac{2}{x+3}+\dfrac{x^2-5x-3}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{3\left(x+3\right)+2\left(x-3\right)+x^2-5x-3}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{3x+9+2x-6+x^2-5x-3}{\left(x-3\right)\left(x+3\right)}=\dfrac{x^2}{\left(x-3\right)\left(x+3\right)}\)
c: \(A\cdot B=\left(x+3\right)\cdot\dfrac{x^2}{\left(x-3\right)\left(x+3\right)}=\dfrac{x^2}{x-3}\)

Câu 4:
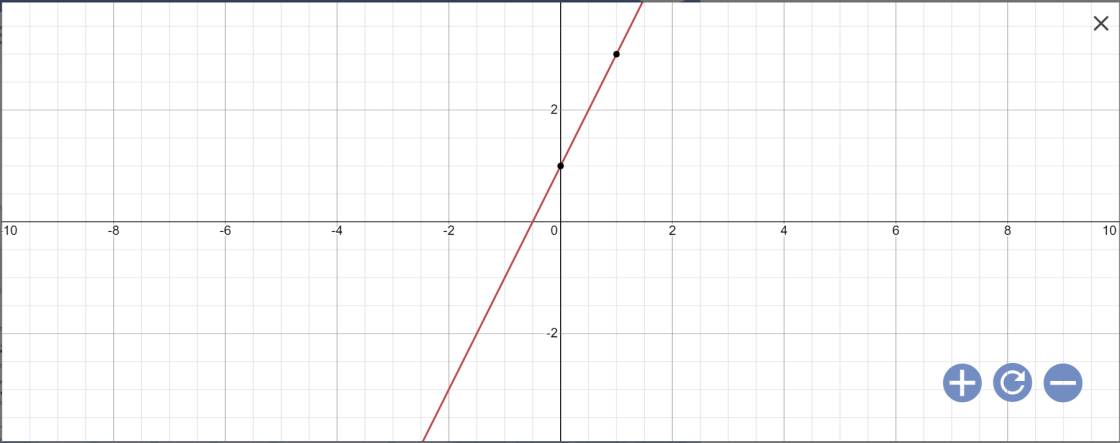
a: Thay m=2 vào y=2x+m-1, ta được:
y=2x+2-1=2x+1
Vẽ đồ thị:
b: Thay x=1 và y=3 vào y=2x+m-1, ta được:
m-1+2=3
=>m+1=3
=>m=2
c: Thay y=0 vào y=x-1, ta được:
x-1=0
=>x=1
Thay x=1 và y=0 vào y=2x+m-1, ta được:
\(2\cdot1+m-1=0\)
=>m+1=0
=>m=-1
Câu 2:
a: \(3\left(x-1\right)-2x+4=4\left(x-2\right)\)
=>\(4x-8=3x-3-2x+4\)
=>\(4x-8=x+1\)
=>3x=9
=>x=3
b: \(\left(x-2\right)\left(3-4x\right)+x^2-4x+4=0\)
=>\(\left(x-2\right)\left(3-4x\right)+\left(x-2\right)^2=0\)
=>\(\left(x-2\right)\left(3-4x+x-2\right)=0\)
=>(x-2)(1-3x)=0
=>\(\left[{}\begin{matrix}x=2\\x=\dfrac{1}{3}\end{matrix}\right.\)
c: ĐKXĐ: \(x\notin\left\{2;-2\right\}\)
\(\dfrac{x+2}{x-2}-\dfrac{x-2}{x+2}=\dfrac{4x^2}{x^2-4}\)
=>\(\dfrac{\left(x+2\right)^2-\left(x-2\right)^2}{\left(x-2\right)\left(x+2\right)}=\dfrac{4x^2}{\left(x-2\right)\left(x+2\right)}\)
=>\(4x^2=x^2+4x+4-x^2+4x-4\)
=>\(4x^2=8x\)
=>\(x^2=2x\)
=>x(x-2)=0
=>\(\left[{}\begin{matrix}x=0\left(nhận\right)\\x=2\left(loại\right)\end{matrix}\right.\)

a: Xét tứ giác AHKM có \(\widehat{AHM}=\widehat{AKM}=90^0\)
nên AHKM là tứ giác nội tiếp
b: Xét (O) có
ΔMAN nội tiếp
MN là đường kính
Do đó: ΔMAN vuông tại A
Xét (O) có
\(\widehat{ABM}\) là góc nội tiếp chắn cung AM
\(\widehat{ANM}\) là góc nội tiếp chắn cung AM
Do đó: \(\widehat{ABM}=\widehat{ANM}\)
Xét ΔHBA vuông tại H và ΔANM vuông tại A có
\(\widehat{HBA}=\widehat{ANM}\)
Do đó: ΔHBA~ΔANM
c: Xét ΔHAB vuông tại H và ΔKMA vuông tại K có
\(\widehat{HAB}=\widehat{KMA}\)(ΔHBA~ΔANM)
Do đó: ΔHAB~ΔKMA
=>\(\dfrac{AH}{MK}=\dfrac{HB}{AK}\)
=>\(AH\cdot AK=MK\cdot HB\)

Ta biết:\(\dfrac{11}{17}\)<\(\dfrac{a}{b}< \dfrac{23}{29}\) và \(8b-9a=31\)(\(a,b\in N\))
\(\Rightarrow b=\dfrac{31+9a}{8}=\dfrac{32-1+8a+a}{8}=\left[\left(4+a\right)+\dfrac{a-1}{8}\right]\in N\)
⇒\(\dfrac{a-1}{8}\in N\)
\(\Leftrightarrow\left(a-1\right)⋮8\Rightarrow a=8k++1\)
khi đó\(b=\dfrac{31+9.\left(8k+1\right)}{8}=9k+5\)⇒\(\dfrac{11}{17}< \dfrac{8k+1}{9k+5}< \dfrac{23}{29}\)
11.(9k+5)<17.(8k+1)⇔k>129.(8k+1)<23.(9k+5)⇔k<4⇒1<k<4
⇒kϵ{2;3}
k=2=>a=17
b=23
k=3=>a=25
b=32
kết luận:(a,b) là:(17,23);(25,32)

\(\text{Δ}=\left[-2\left(m-1\right)\right]^2-4\left(m^2-3m\right)\)
\(=4m^2-8m+4-4m^2+12m=4m+4\)
Để phương trình có hai nghiệm phân biệt thì 4m+4>0
=>m>-1
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2\left(m-1\right)=2m-2\\x_1x_2=\dfrac{c}{a}=m^2-3m\end{matrix}\right.\)
\(\dfrac{1}{x_1^2}+\dfrac{1}{x_2^2}=4\)
=>\(\dfrac{x_1^2+x_2^2}{\left(x_1x_2\right)^2}=4\)
=>\(\dfrac{\left(x_1+x_2\right)^2-2x_1x_2}{\left(x_1x_2\right)^2}=4\)
=>\(\left(2m-2\right)^2-2\left(m^2-3m\right)=4\left(m^2-3m\right)^2\)
=>\(4m^2-8m+4-2m^2+6m=4\left(m^2-3m\right)^2\)
=>\(2m^2-2m+4=4\left(m^2-3m\right)^2\)
=>\(2\left(m^4-6m^2+9\right)=m^2-m+2\)
=>\(2m^4-12m^2+18-m^2+m-2=0\)
=>\(2m^4-13m^2+m+16=0\)
=>\(m\in\left\{-2,27;-1,21;1,37;2,12\right\}\)


Bài 2:
a: 7-3x=9-x
=>-3x+x=9-7
=>-2x=2
=>x=-1
b: \(\dfrac{x+2}{3}+\dfrac{3x-1}{5}=-2\)
=>\(\dfrac{5\left(x+2\right)+3\left(3x-1\right)}{15}=-2\)
=>\(5\left(x+2\right)+3\left(3x-1\right)=-30\)
=>5x+10+9x-3=-30
=>14x+7=-30
=>14x=-37
=>\(x=-\dfrac{37}{14}\)
Bài 1:
a:
(d): y=x+2
=>Hệ số góc là a=1>0
=>Góc tạo bởi (d) với trục Ox là góc nhọn
b: (d')//(d)
=>\(\left\{{}\begin{matrix}a=1\\2\ne-2\left(đúng\right)\end{matrix}\right.\)
=>a=1
c: