Tìm số tự nhiên a biết khi chia a cho 15;21;25 thì số dư lần lượt là 7;10;12 và 1000<a<1100
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


(x - 3)⁴ = (x - 3)²
(x - 3)⁴ - (x - 3)² = 0
(x - 3)².[(x - 3)² - 1] = 0
(x - 3)².(x² - 6x + 9 - 1) = 0
(x - 3)²(x² - 6x + 8) = 0
(x - 3)²(x² - 2x - 4x + 8) = 0
(x - 3)²[(x² - 2x) - (4x - 8)] = 0
(x - 3)²[x(x - 2) - 4(x - 2)] = 0
(x - 3)²(x - 2)(x - 4) = 0
(x - 3)² = 0 hoặc x - 2 = 0 hoặc x - 4 = 0
*) (x - 3)² = 0
x - 3 = 0
x = 3
*) x - 2 = 0
x = 2
*) x - 4 = 0
x = 4
Vậy x = 2; x = 3; x = 4

Sửa đề: số học sinh khối 6 của trường từ 660 đến 720 học sinh
Giải
Gọi x (học sinh) là số học sinh cần tìm (x ∈ ℕ* và 660 ≤ x ≤ 720)
Do khi xếp hàng 10; 12; 15 đều vừa đủ nên x ∈ BC(10; 12; 15)
Ta có:
10 = 2.5
12 = 2².3
15 = 3.5
⇒ BCNN(10; 12; 15) = 2².3.5 = 60
⇒ x ∈ BC(10; 12; 15) = B(60) = {0; 60; ...; 600; 660; 720; ...}
Do 660 chia 18 dư 12 nên x = 660
Vậy số học sinh cần tìm là 660 học sinh

x + 5 = x + 1 + 4
Do x là số tự nhiên nên x + 1 > 1
Để (x + 5) ⋮ (x + 1) thì 4 ⋮ (x + 1)
x + 1 ∈ Ư(4) = {2; 4}
⇒ x ∈ {1; 3}
x + 5 = x + 1 + 4
Do x là số tự nhiên nên x + 1 > 1
Để (x + 5) ⋮ (x + 1) thì 4 ⋮ (x + 1)
x + 1 ∈ Ư(4) = {2; 4}
⇒ x ∈ {1; 3}

2\(xy\) + 4\(x\) + y + 2 = 4 + 2
2\(x\).( y + 2) + (y + 2) = 6
(y + 2).(2\(x\) + 1) = 6
Ư(6) = {-6; -3; -2; -1; 1; 2; 3; 6}
Lập bảng ta có:
| 2\(x+1\) | -6 | -3 | -2 | -1 | 1 | 2 | 3 | 6 |
| \(x\) | -\(\dfrac{7}{2}\) | -2 | -\(\dfrac{3}{2}\) | -1 | 0 | \(\dfrac{1}{2}\) | 1 | \(\dfrac{7}{2}\) |
| y + 2 | -1 | -2 | -3 | -6 | 6 | 3 | 2 | 1 |
| y | -3 | -4 | -5 | -8 | 4 | 1 | 0 | -1 |
Theo bảng trên ta có các cặp (\(x\);y) nguyên thỏa mãn đề bài là:
(\(x\); y) = (-2; -4); (-1; -8); (0; 4); (1; 0)

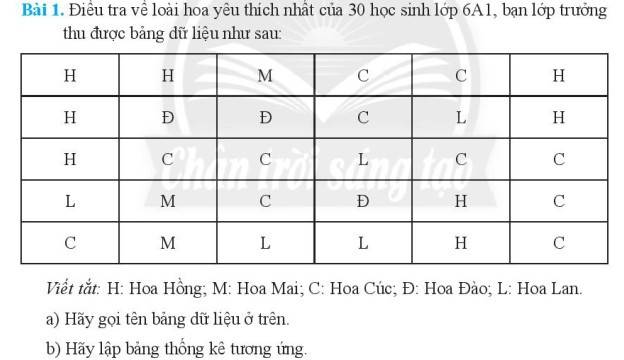
a, Điều tra về loài hoa yêu thích của 30 học sinh lớp 6 A1
b, Bảng dữ liệu điều tra về loài hoa yêu thích nhất của 30 học sinh lớp 6A1
| Số học sinh yêu thích hoa | Tên loài hoa được học sinh yêu thích |
| 8 | Hoa Hồng |
| 3 | Hoa Mai |
| 11 | Hoa Cúc |
| 3 | Hoa Đào |
| 5 | Hoa Lan |

Bài 6: \(x\).(\(x\) + 2) < 0
Lập bảng xét dấu ta có:
| \(x\) | -2 0 |
| \(x\) | - + + |
| \(x\) + 2 | - 0 - 0 + |
| \(x\).(\(x\) + 2) | + 0 - 0 + |
- 2 < \(x\) < 0
Vì \(x\) nguyên nên \(x\) = -1
b, (7 - \(x\)).(\(x\) + 3) > 0
Lập bảng ta có:
| \(x\) | -3 7 |
| 7 - \(x\) | + + 0 - |
| \(x\) + 3 | - 0 + + |
| (7 - \(x\)).(\(x\) + 3) | - 0 + 0 - |
- 3 < \(x\) < 7
Vì \(x\) \(\in\) Z nên \(x\) \(\in\) {-2; -1; 0; 1; 2; 3; 4; 5; 6}

\(a,\left(8-2x\right)\left(3+x\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}8-2x=0\\3+x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=8\\x=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-3\end{matrix}\right.\\ ---\\ b,\left(2x+1\right)^2=25\\ Mà:5^2=25;\left(-5\right)^2=25\\ \Rightarrow\left[{}\begin{matrix}\left(2x+1\right)^2=5^2\\\left(2x+1\right)^2=\left(-5\right)^2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x+1=5\\2x+1=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=4\\2x=-6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-3\end{matrix}\right.\)
\(----\\ c,\left(1-3x\right)^3=64=4^3\\ Nên:1-3x=4\\ \Leftrightarrow3x=-3\\ \Leftrightarrow x=-1\)
\(d,\left(4-x\right)^3=-27\\ Mà:\left(-3\right)^3=-27\\ Nên:\left(4-x\right)^3=\left(-3\right)^3\\ Nên:4-x=-3\\ Vậy:x=4+3=7\\ Vậy:x=7\\ ---\\ e,\left(x^2-1\right)\left(5-x\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x^2-1=0\\5-x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x^2=1\\x=5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\pm1\\x=5\end{matrix}\right.\\ ---\\ g,x^2-4x=0\\ \Leftrightarrow x\left(x-4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)

\(Thay:a=-1;b=1.vàoA:\\ A=5a^3b^8=5.\left(-1\right)^3.1^8=5.\left(-1\right).1=-5\\ --\\ Thay:a=-1;b=2.vàoB:\\ B=-9a^4-b^2=-9.\left(-1\right)^4-2^2=-9.1-4=-9-4=-13\)

Lời giải:
$a=1+2+3+...+n=\frac{n(n+1)}{2}$
Gọi $ƯCLN(a,b)=d$ thì:
$\frac{n(n+1)}{2}\vdots d$
$2n+1\vdots d$
$\Rightarrow n(n+1)\vdots d; 2n+1\vdots d$
Từ $n(n+1)\vdots d$, mà $(n,n+1)=1$ nên:
$n\vdots d$ hoặc $n+1\vdots d$
Nếu $n\vdots d\Rightarrow 2n\vdots d$
Kết hợp với $2n+1\vdots d\Rightarrow 1\vdots d$
$\Rightarrow d=1$
Nếu $n+1\vdots d\Rightarrow 2n+2\vdots d$
Kết hợp với $2n+1\vdots d$
$\Rightarrow (2n+2)-(2n+1)\vdots d$
Hay $1\vdots d\Rightarrow d=1$
Vậy $ƯCLN(a,b)=1$
 Câu b là vẽ nha .
Câu b là vẽ nha . 
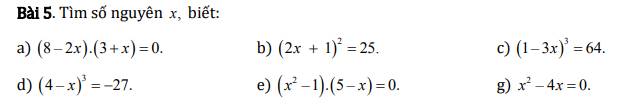

a:15�:15 dư 13 ⇒a=15k+13(k∈N )⇒�=15�+13(�∈� )
b:12�:12 dư 8 ⇒b=12k+8(k∈N)⇒�=12�+8(�∈�)
⇒a+b=15k+12k+13+8=27k+21=3(9k+7)
Chúc bạn học tốt :3