tìm x,y biết:
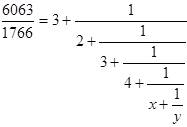
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\left|x-1\right|+\dfrac{4}{3}=4\dfrac{2}{3}\)
\(\Leftrightarrow\left|x-1\right|+\dfrac{4}{3}=\dfrac{14}{3}\)
\(\Leftrightarrow\left|x-1\right|=\dfrac{10}{3}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=\dfrac{10}{3}\\x-1=-\dfrac{10}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{13}{3}\\x=-\dfrac{7}{3}\end{matrix}\right.\)
|x-1| +4/3= 14/3
|x-1| = 14/3-4/3=10/3
x-1 = ±10/3
TH1: x-1 =10/3
x = 10/3 + 1=13/3
TH2: x-1 = -10/3
x =-10/3+1=-13/3
Vậy x =13/3 hoạc x=-13/3

Biết 36 người làm cỏ một cánh đồng hết 8 giờ. Nếu muốn hoàn thành sớm hơn 2 giờ thì số người cần thêm vào là

Lời giải:
a. Xét tam giác $AOI$ và $BOI$ có:
$OA=OB$ (gt)
$\widehat{AOI}=\widehat{BOI}$ (do $OI$ là tia phân giác $\widehat{AOB}$)
$OI$ chung
$\Rightarrow \triangle AOI=\triangle BOI$ (c.g.c)
b.
Giả sử $AB$ cắt $OI$ tại $M$
Xét tam giác $AOM$ và $BOM$ có:
$AO=BO$ (gt)
$\widehat{AOM}=\widehat{BOM}$
$OM$ chung
$\Rightarrow \triangle AOM=\triangle BOM$ (c.g.c)
$\Rightarrow \widehat{AMO}=\widehat{BMO}$
Mà $\widehat{AMO}+\widehat{BMO}=\widehat{AMB}=180^0$
$\Rightarrow \widehat{AMO}=\widehat{BMO}=90^0$
$\Rightarrow AB\perp OI$

Bạn nên tách lẻ bài ra 1 bài/ 1 post để được hỗ trợ tốt hơn.

Áp dụng tính chất dãy tỉ số bằng nhau ta có:
$\dfrac x9 = \dfrac y8 = \dfrac{x+y}{9 +8} = \dfrac{-17}{17} = -1$
Suy ra $x = (-1). 9 = -9$ và $y = (-1).8 = -8$.
Em sẽ áp dụng tính chất dãy tỉ số bằng nhau nhé, ví dụ: $\dfrac{x_1}{y_1} = \dfrac{x_2}{y_2} = \dfrac{x_1 + x_2}{y_1 + y_2} = \dfrac{x_1 - x_2}{y_1 - y_2}$ (các biểu thức đều có nghĩa).
Đề bài cho tổng $x + y = -17$ nên:
$\dfrac x9 = \dfrac y8 = \dfrac{x+y}{8+9} = \dfrac{-17}{17} = -1$.
Từ đó em suy ra $x$; $y$ nhé.
$\dfrac x9 = -1$ thì $x = (-1).9 = -9.$ Tương tự ta tìm được $y$.
Để hiểu hơn về các bài dạng này, em theo dõi bài học này trên OLM nhé: https://olm.vn/chu-de/tinh-chat-cua-day-ti-so-bang-nhau-2132348726
\(\dfrac{6063}{1766}=3+\dfrac{1}{2+\dfrac{1}{3+\dfrac{1}{4+\dfrac{1}{x+\dfrac{1}{y}}}}}\)
\(3\dfrac{765}{1766}=3+\dfrac{1}{2+\dfrac{1}{3+\dfrac{1}{4+\dfrac{1}{x+\dfrac{1}{y}}}}}\)
\(\dfrac{765}{1766}=\dfrac{1}{2+\dfrac{1}{3+\dfrac{1}{4+\dfrac{1}{x+\dfrac{1}{y}}}}}\)
\(\dfrac{1766}{765}=2+\dfrac{1}{3+\dfrac{1}{4+\dfrac{1}{x+\dfrac{1}{y}}}}\)
\(2\dfrac{236}{765}=2+\dfrac{1}{3+\dfrac{1}{4+\dfrac{1}{x+\dfrac{1}{y}}}}\)
\(\dfrac{236}{765}=\dfrac{1}{3+\dfrac{1}{4+\dfrac{1}{x+\dfrac{1}{y}}}}\)
\(\dfrac{765}{236}=3+\dfrac{1}{4+\dfrac{1}{x+\dfrac{1}{y}}}\)
\(3\dfrac{57}{236}=3+\dfrac{1}{4+\dfrac{1}{x+\dfrac{1}{y}}}\)
\(\dfrac{57}{236}=\dfrac{1}{4+\dfrac{1}{x+\dfrac{1}{y}}}\)
\(\dfrac{236}{57}=4+\dfrac{1}{x+\dfrac{1}{y}}\)
\(4\dfrac{8}{57}=4+\dfrac{1}{x+\dfrac{1}{y}}\)
\(\dfrac{8}{57}=\dfrac{1}{x+\dfrac{1}{y}}\)
\(\dfrac{57}{8}=x+\dfrac{1}{y}\)
\(\dfrac{57}{8}=\dfrac{xy+1}{y}\)
\(\left(\dfrac{xy+1}{y}\right)làphânsốtốigiản\)
=> y = 8
=> xy+1 = 57
=> 8x + 1 =57
=> 8x = 56
=> x = 56/8=7
Vậy x = 7 và y = 8