
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét tứ giác EAOD có \(\widehat{EAO}+\widehat{EDO}=90^0+90^0=180^0\)
nên EAOD là tứ giác nội tiếp
b: Xét (O) có
EA,ED là các tiếp tuyến
Do đó: EA=ED
=>E nằm trên đường trung trực của AD(1)
ta có: OA=OD
=>O nằm trên đường trung trực của AD(2)
Từ (1),(2) suy ra OE là đường trung trực của AD
=>OE\(\perp\)AD tại H
Xét (O) có
ΔAKB nội tiếp
AB là đường kính
Do đó: ΔAKB vuông tại K
Xét ΔEAB vuông tại A có AK là đường cao
nên \(EK\cdot EB=EA^2\left(3\right)\)
Xét ΔEAO vuông tại A có AH là đường cao
nên \(EH\cdot EO=EA^2\left(4\right)\)
Từ (3),(4) suy ra \(EK\cdot EB=EH\cdot EO\)

\(B=\left(\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1}-\dfrac{\sqrt{x}-2}{x-1}\right)\cdot\dfrac{x\sqrt{x}+x-\sqrt{x}-1}{\sqrt{x}}\)
\(=\left(\dfrac{\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2}-\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\cdot\dfrac{\left(\sqrt{x}+1\right)\left(x-1\right)}{\sqrt{x}}\)
\(=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)-\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)^2\cdot\left(\sqrt{x}-1\right)}\cdot\dfrac{\left(\sqrt{x}+1\right)^2\cdot\left(\sqrt{x}-1\right)}{\sqrt{x}}\)
\(=\dfrac{x+\sqrt{x}-2-\left(x-\sqrt{x}-2\right)}{\sqrt{x}}=\dfrac{2\sqrt{x}}{\sqrt{x}}=2\)
=>B là số nguyên

a: Thay x=1 và y=1 vào (d), ta được:
\(a\cdot1+3=1\)
=>a+3=1
=>a=-2
b: a=-2 nên y=-2x+3
Thay x=-2 vào y=-2x+3, ta được:
\(y=-2\cdot\left(-2\right)+3=7=y_B\)
Vậy: B(-2;7) thuộc (d)
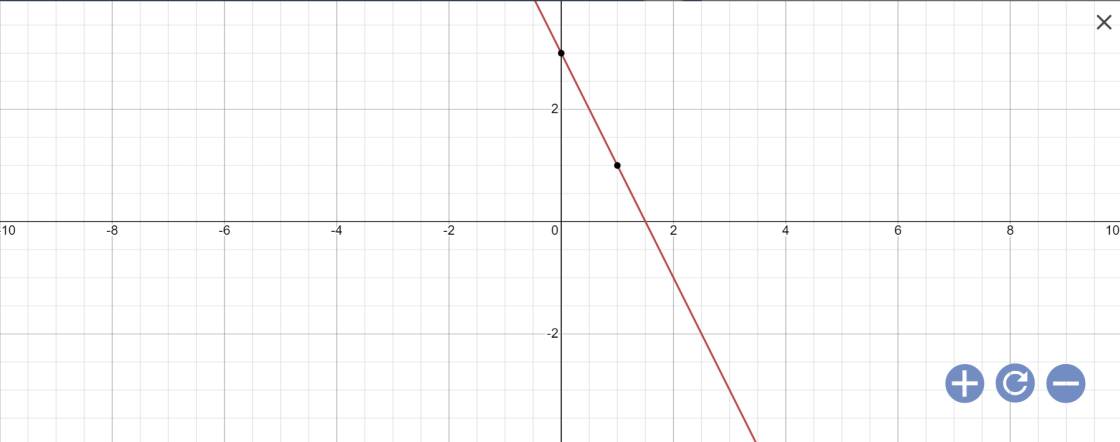
c: y=-2x+3

Lời giải:
Gọi tia sáng mặt trời tạo với mặt đất là $\alpha$.
Ta có:
$\tan \alpha = \frac{7,5}{12}=\frac{5}{8}$
$\Rightarrow \alpha = 32^0$

\(\Delta=m^2-4\left(m-1\right)=\left(m-2\right)^2\ge0;\forall m\in\mathbb{R}\)
\(\Rightarrow\) Phương trình đã cho có 2 nghiệm với mọi \(m\in\mathbb{R}\)
Theo hệ thức Vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=-m\\x_1x_2=m-1\end{matrix}\right.\)
Theo đề bài, ta có:
\(x_1^3+x_2^3=26\)
\(\Leftrightarrow\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=26\)
\(\Rightarrow\left(-m\right)^3-3\left(m-1\right)\cdot\left(-m\right)=26\)
\(\Leftrightarrow-m^3+3m-3=26\)
\(\Leftrightarrow m^3-3m+29=0\)
Nghiệm của pt này hơi xấu, bạn kiểm tra lại đề nhé.
Từ trên xuống tới dòng:
(-m)³ - 3(m - 1).(-m) = 26 em coi của bạn Toru nhé, Thầy giải tiếp chỗ đó
(-m)³ - 3(m - 1).(-m) = 26
⇔ -m³ + 3m² - 3m = 26
⇔ m³ - 3m² + 3m + 26 = 0
⇔ m³ + 2m² - 5m² - 10m + 13m + 26 = 0
⇔ (m³ + 2m²) - (5m² + 10m) + (13m + 26) = 0
⇔ m²(m + 2) - 5m(m + 2) + 13(m + 2) = 0
⇔ (m + 2)(m² - 5m + 13) = 0
⇔ m + 2 = 0 hoặc m² - 5m + 13 = 0
*) m + 2 = 0
⇔ m = -2
*) m² - 5m + 13 = 0 (2)
∆ = (-5)² - 4.1.13 = -27 < 0
⇒ Phương trình (2) vô nghiệm
Vậy m = -2

\(\text{Δ}=m^2-4\cdot1\cdot\left(m-1\right)\)
\(=m^2-4m+4=\left(m-2\right)^2>=0\forall m\)
=>Phương trình luôn có hai nghiệm
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-m\\x_1x_2=\dfrac{c}{a}=m-1\end{matrix}\right.\)
\(x_1^3+x_2^3=26\)
=>\(\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=26\)
=>\(\left(-m\right)^3-3\cdot\left(-m\right)\left(m-1\right)=26\)
=>\(-m^3+3m\left(m-1\right)=26\)
=>\(m^3-3m\left(m-1\right)=-26\)
=>\(m^3-3m^2+3m=-26\)
=>\(m^3-3m^2+3m-1=-27\)
=>\(\left(m-1\right)^3=-27\)
=>m-1=-3
=>m=-2

a: Thay m=1 vào (1), ta được:
\(\left\{{}\begin{matrix}x+2y=1+3=4\\2x-3y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+4y=8\\2x-3y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}7y=7\\x+2y=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=1\\x=2\end{matrix}\right.\)
b: Vì \(\dfrac{1}{2}\ne\dfrac{2}{-3}\)
nên hệ (1) luôn có nghiệm duy nhất
\(\left\{{}\begin{matrix}x+2y=m+3\\2x-3y=m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+4y=2m+6\\2x-3y=m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+4y-2x+3y=2m+6-m\\x+2y=m+3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}7y=m+6\\x=m+3-2y\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=\dfrac{m+6}{7}\\x=m+3-\dfrac{2\left(m+6\right)}{7}=\dfrac{7m+21-2m-12}{7}=\dfrac{5m+9}{7}\end{matrix}\right.\)
x+y=-3
=>\(\dfrac{5m+9+m+6}{7}=-3\)
=>6m+15=-21
=>6m=-36
=>m=-6

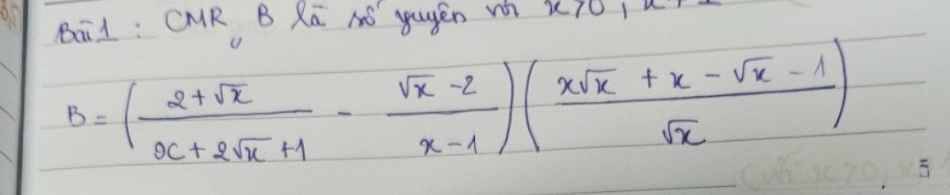 giúp e bài này với ạ
giúp e bài này với ạ 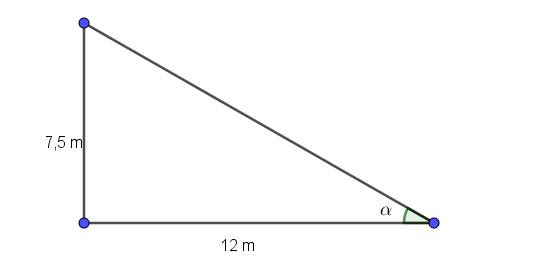
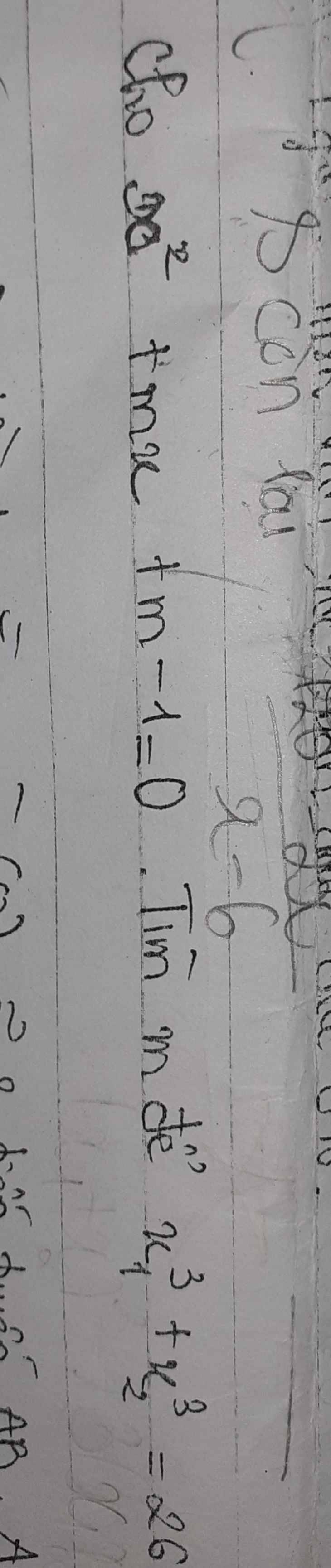
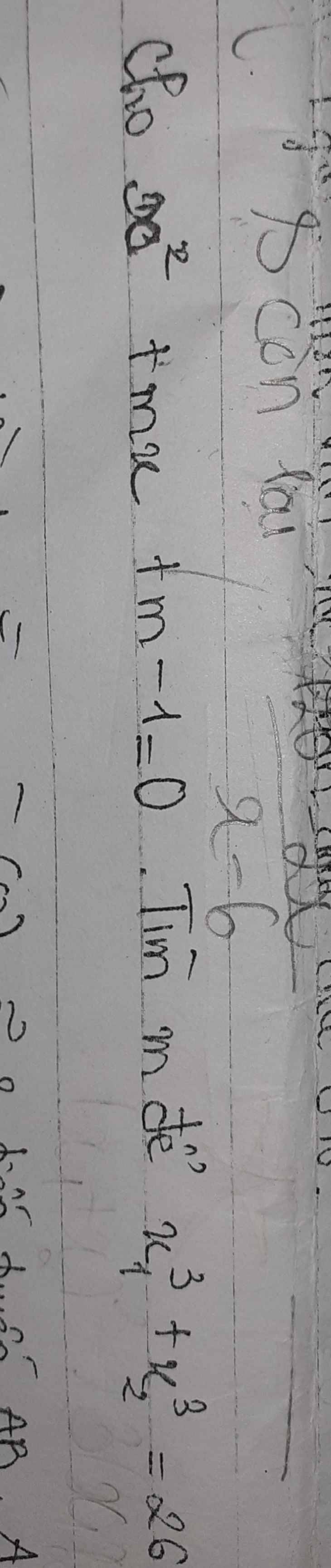

Bài 1:
1: Thay x=2025 vào A, ta được:
\(A=\dfrac{2025+5}{\sqrt{2025}-2}=\dfrac{2030}{43}\)
2: \(B=\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{2}{\sqrt{x}+2}-\dfrac{4\sqrt{x}}{x-4}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{2}{\sqrt{x}+2}-\dfrac{4\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)-2\left(\sqrt{x}-2\right)-4\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{x+2\sqrt{x}-2\sqrt{x}+4-4\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{x-4\sqrt{x}+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\)
3: \(P=A\cdot B=\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\cdot\dfrac{x+5}{\sqrt{x}-2}=\dfrac{x+5}{\sqrt{x}+2}\)
\(=\dfrac{x-4+9}{\sqrt{x}+2}=\sqrt{x}-2+\dfrac{9}{\sqrt{x}+2}\)
\(=\sqrt{x}+2+\dfrac{9}{\sqrt{x}+2}-4>=2\cdot\sqrt{\left(\sqrt{x}+2\right)\cdot\dfrac{9}{\sqrt{x}+2}}-4=2\)
Dấu '=' xảy ra khi \(\sqrt{x}+2=\sqrt{9}=3\)
=>x=1(nhận)
Bài 3:
1: Khi m=-2 thì phương trình sẽ trở thành:
\(x^2+2\cdot\left(-2\right)\cdot x-2-3=0\)
=>\(x^2-4x-5=0\)
=>(x-5)(x+1)=0
=>\(\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)
2: \(\text{Δ}=\left(2m\right)^2-4\cdot1\cdot\left(m-3\right)\)
\(=4m^2-4m+12=4m^2-4m+1+11=\left(2m-1\right)^2+11>0\forall m\)
=>Phương trình luôn có 2 nghiệm phân biệt
Theo vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-2m\\x_1x_2=\dfrac{c}{a}=m-3\end{matrix}\right.\)
\(x_1^2+x_1x_2-2x_2^2=3\left(x_1-x_2\right)\)
=>\(x_1^2+2x_1x_2-x_1x_2-2x_2^2=3\left(x_1-x_2\right)\)
=>\(x_1\left(x_1+2x_2\right)-x_2\left(x_1+2x_2\right)-3\left(x_1-x_2\right)=0\)
=>\(\left(x_1-x_2\right)\left(x_1+2x_2-3\right)=0\)
=>\(\left[{}\begin{matrix}x_1=x_2\\x_1+2x_2=3\end{matrix}\right.\)
TH1: \(x_1=x_2\)
mà \(x_1+x_2=-2m\)
nên \(x_1=x_2=-m\)
\(x_1x_2=m-3\)
=>\(\left(-m\right)\cdot\left(-m\right)=m-3\)
=>\(m^2-m+3=0\)
=>\(\left(m-\dfrac{1}{2}\right)^2+\dfrac{11}{4}=0\)(vô lý)
TH2: \(x_1+2x_2=3\)
mà \(x_1+x_2=-2m\)
nên \(x_2=3-\left(-2m\right)=2m+3\)
=>\(x_1=-2m-x_2=-2m-\left(2m+3\right)=-4m-3\)
\(x_1x_2=m-3\)
=>\(\left(2m+3\right)\left(-4m-3\right)=m-3\)
=>\(-8m^2-6m-12m-9=m-3\)
=>\(-8m^2-18m-9-m+3=0\)
=>\(-8m^2-19m-6=0\)
=>\(\left[{}\begin{matrix}m=-\dfrac{3}{8}\\m=-2\end{matrix}\right.\)