Giải rõ Câu 5 giúp mình với ạ 😞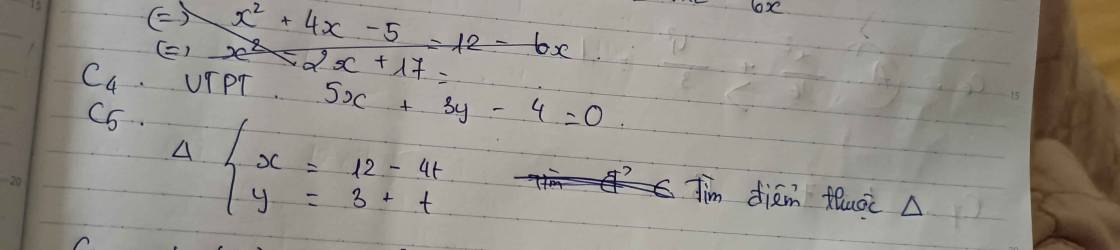
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Có \(\left|\Omega\right|=C^4_{25}\)
Gọi A là biến cố: "Có ít nhất 1 viên bi màu đỏ."
Xét biến cố \(\overline{A}:\) "Không có viên bi màu đỏ nào."
Khi đó \(\left|\overline{A}\right|=C^4_{15}\) \(\Rightarrow P\left(\overline{A}\right)=\dfrac{C^4_{15}}{C^4_{25}}=\dfrac{273}{2530}\)
\(\Rightarrow P\left(A\right)=1-P\left(\overline{A}\right)=1-\dfrac{273}{2530}=\dfrac{2257}{2530}\)


Gọi các số thỏa mãn ycbt là \(\overline{\alpha\beta\gamma\delta}\)
Khi đó \(\delta\in\left\{4,6,8\right\}\) -> Có 3 cách.
TH1: \(\alpha,\beta,\gamma\) đều lẻ \(\Rightarrow\) Có \(A^3_4=24\) cách.
TH2: Trong các số \(\alpha,\beta,\gamma\) có đúng 1 số chẵn
\(\Rightarrow\) Có \(3.2.4.3=72\) cách.
TH3: Trong các số \(\alpha,\beta,\gamma\) có đúng 1 số lẻ.
\(\Rightarrow\) Có \(3.4.2.1=24\) cách.
\(\Rightarrow\) Có tất cả \(24+72+24=120\) cách chọn bộ \(\left(\alpha,\beta,\gamma\right)\)
\(\Rightarrow\) Có tất cả \(3.120=360\) số thỏa mãn ycbt.

Câu a là lấy mấy viên để xác suất có 3 viên đỏ em? Đề bài thiếu.
b.
Không gian mẫu: \(C_{20}^4\)
Số cách lấy 2 viên đỏ, 2 viên xanh: \(C_{12}^2.C_8^2\)
Xác suất: \(P=\dfrac{C_{12}^2.C_8^2}{C_{20}^2}=\)
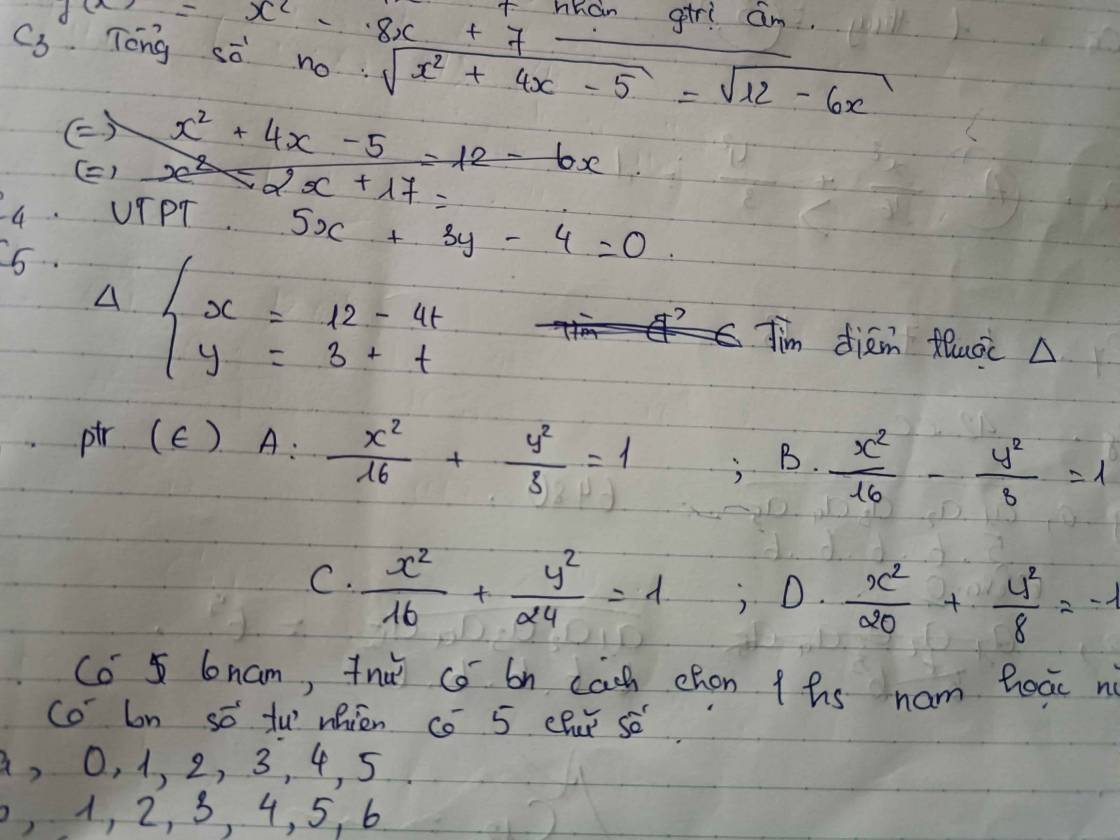

Câu 5:
\(\left\{{}\begin{matrix}x=12-4t\\y=3+t\end{matrix}\right.\)(Δ)
=>\(A\left(12-4t;3+t\right)\left(t\in R\right)\) là những điểm thuộc Δ