Cho ∆ABC cân tại A(𝐴̂ < 90 độ ), M là trung điểm của BC.
a) Chứng minh ∆ABM = ∆ACM.
b) Trên cạnh AM lấy điểm D bất kỳ (D khác A và M). Chứng minh: ∆ADB = ∆ADC.Từ đó suy ra DB = DC.
c) Trên tia đối của tia DB lấy điểm E sao cho DB = DE. Gọi G là điểm trên đoạn thẳng CD sao cho CG 2/3 = CD. Chứng minh: ba điểm M, G, E thẳng hàng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số công nhân trong đội lúc đầu là $x$.
Theo đề bài, ta có:
$x \cdot 30 = (x + 10) \cdot 20$
Giải trên, ta được: $x = 20$
Vậy, số công nhân trong đội lúc đầu là 20 người.

Gọi giá tiền mua 1 kg táo, 1kg bưởi và 1 kg dưa hấu lần lượt là a(đồng),b(đồng),c(đồng)
Vì số tiền để cô Mai mua táo bằng số tiền mua bưởi và dưa hấu nên 3a=6b=10c
=>\(\dfrac{3a}{30}=\dfrac{6b}{30}=\dfrac{10c}{30}\)
=>\(\dfrac{a}{10}=\dfrac{b}{5}=\dfrac{c}{3}\)
Giá 1kg bưởi hơn 1kg dưa hấu 18000 đồng nên b-c=18000
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{10}=\dfrac{b}{5}=\dfrac{c}{3}=\dfrac{b-c}{5-3}=\dfrac{18000}{2}=9000\)
=>\(a=9000\cdot10=90000;b=9000\cdot5=45000;c=9000\cdot3=27000\)
Vậy: giá tiền mua 1 kg táo, 1kg bưởi và 1 kg dưa hấu lần lượt là 90000 đồng; 45000 đồng; 27000 đồng

a: Sửa đề: ΔBAD=ΔBED
Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
b: Xét ΔMDH và ΔMCB có
\(\widehat{MDH}=\widehat{MCB}\)(hai góc so le trong, DH//BC)
MD=MC
\(\widehat{DMH}=\widehat{CMB}\)(hai góc đối đỉnh)
Do đó: ΔMDH=ΔMCB
=>DH=CB

a)Ta có tam giác ABC cân
=>:AB=AC;góc B=góc C.
Xét tam giác AMB và tam giác AMC có:
AB=AC(cmt)
góc BAM=góc CAM (AM là phân giác của góc A).
AM chung.
=>tam giác AMB = tam giác AMC(c-g-c)
b) Vì tam giác AMB = tam giác AMC
=>góc AMB=góc AMC (2 góc tương ứng)
Mà 2 góc ở vị trí kề bù => góc AMB=góc AMC=180:2=90độ
=>AM vuông góc BC
c)

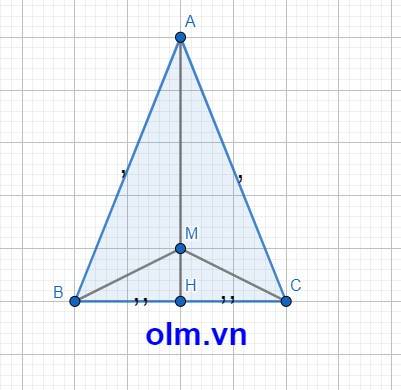
Nếu M là điểm tùy ý trên AH thì BM = MC chứ không phải BM = BA em nhé.

Gọi O là giao điểm của AE và BI.
Do I là trung điểm của AC nên AI = IC.
Gọi H là hình chiếu của I lên BC.
Do HI vuông góc với BC nên tam giác BHI và CHI là các tam giác vuông cân tại I.
Trong tam giác BHI, ta có $$BH^2 + IH^2 = BI^2$$.
Trong tam giác CHI, ta có $$CH^2 + IH^2 = CI^2$$.
Cộng ta được $$BH^2 + CH^2 + 2IH^2 = BI^2 + CI^2$$.
Nhưng $$BH + CH = BC$$ và $$BI^2 + CI^2 = BC^2$$ (do tam giác BIC là tam giác vuông tại I), nên ta có $$BC^2 + 2IH^2 = BC^2$$.
Điều này chỉ ra rằng $$IH = 0$$, tức là I trùng với H.
Do I trùng với H, điểm I nằm trên BC. Vì vậy, đường thẳng AE (đường thẳng vuông góc với BC tại E) sẽ vuông góc với BI tại I.
Vậy AE vuông góc với BI.

Gọi \(F\) là giao điểm của \(AB\) và \(EI\)
Xét \(\Delta IAF\) và \(\Delta ICE\)
có: \(\widehat{IAF}=\widehat{ICE}=90^o\left(gt\right)\)
\(IA=IC\left(gt\right)\)
\(\widehat{AIF}=\widehat{CIE}\) (đối đỉnh)
\(\Rightarrow\Delta IAF=\Delta ICE\left(g-c-g\right)\)
\(\Rightarrow IF=IE\) (hai cạnh tương ứng)
Xét tứ giác \(AFCE\)
có: \(IA=IC\left(gt\right)\)
\(IF=IE\left(cmt\right)\)
\(\Rightarrow\) Tứ giác \(AFCE\) là hình bình hành
\(\Rightarrow AE//FC\left(1\right)\)
Xét \(\Delta BFC\)
có: \(CI\perp BF\left(gt\right)\)
\(FI\perp BC\left(gt\right)\)
\(\Rightarrow I\) là trực tâm của \(\Delta BFC\)
\(\Rightarrow BI\perp FC\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) \(\Rightarrow AE\perp BI\left(đpcm\right)\)

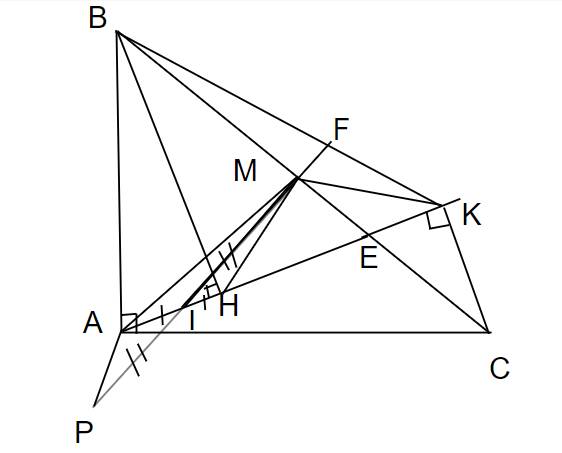
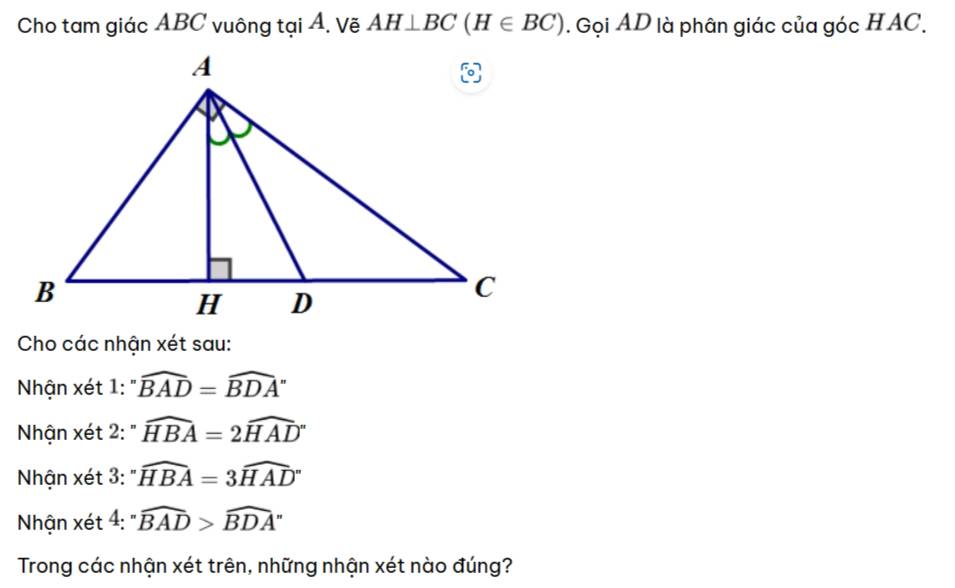
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
b: Ta có: ΔABM=ΔACM
=>\(\widehat{BAM}=\widehat{CAM}\)
Xét ΔADB và ΔADC có
AD chung
\(\widehat{BAD}=\widehat{CAD}\)
AB=AC
Do đó: ΔADB=ΔADC
=>DB=DC
c:
Ta có: DB và DE là hai tia đối nhau
=>D nằm giữa B và E
mà DB=DE
nên D là trung điểm của BE
Xét ΔCEB có
CD là đường trung tuyến
\(CG=\dfrac{2}{3}CD\)
Do đó: G là trọng tâm của ΔCEB
Xét ΔCEB có
G là trọng tâm
M là trung điểm của BC
Do đó; E,G,M thẳng hàng