`@` `\text {Ans}`

`\downarrow`

\(-7\in\text{N}\)

\(-7\in\text{Z}\)

\(-7\in\text{Q}\)

\(-\dfrac{5}{7}\notin\text{Z}\)

\(-\dfrac{5}{7}\in\text{Q}\)

`@` `\text {Ans}`

`\downarrow`

`a)` Đúng

`b)` Đúng

`c)` Sai

`-` Số `0` không phải là số hữu tỉ âm cũng không phải là số hữu tỉ dương.

`d)` Sai

`-` Số nguyên âm cũng được gọi là `1` số hữu tỉ âm, vì tập hợp số nguyên là tập hợp con của tập hợp số hữu tỉ.

a,đúng

b, đúng

c, sai

d, sai 

(\(x-3\))² + (2y - 1)² = 0

          (\(x\) - 3)² ≥ 0 ∀ \(x\)

        (2y - 1)² ≥ 0 ∀ y

⇔ (\(x\) - 3)² + (2y - 1)²= 0

⇔ \(\left\{{}\begin{matrix}x-3=0\\3y-1=0\end{matrix}\right.\)

\(\Leftrightarrow\) \(\left\{{}\begin{matrix}x=2\\y=\dfrac{1}{3}\end{matrix}\right.\)

(4\(x-3\))⁴ + (y + 2)² ≤ 0

(4\(x\) - 3)⁴ ≥ 0 ∀ \(x\)

(y + 2)² ≥ 0 ∀ y

⇔(4\(x\) - 3)⁴   + (y+2)² ≥ 0

⇔ (4\(x\) - 3)⁴ + (y + 2)² ≤ 0 ⇔

⇔\(\left\{{}\begin{matrix}4x-3=0\\y+2=0\end{matrix}\right.\)

⇔ \(\left\{{}\begin{matrix}x=\dfrac{3}{4}\\y=-2\end{matrix}\right.\)

help me :(((((

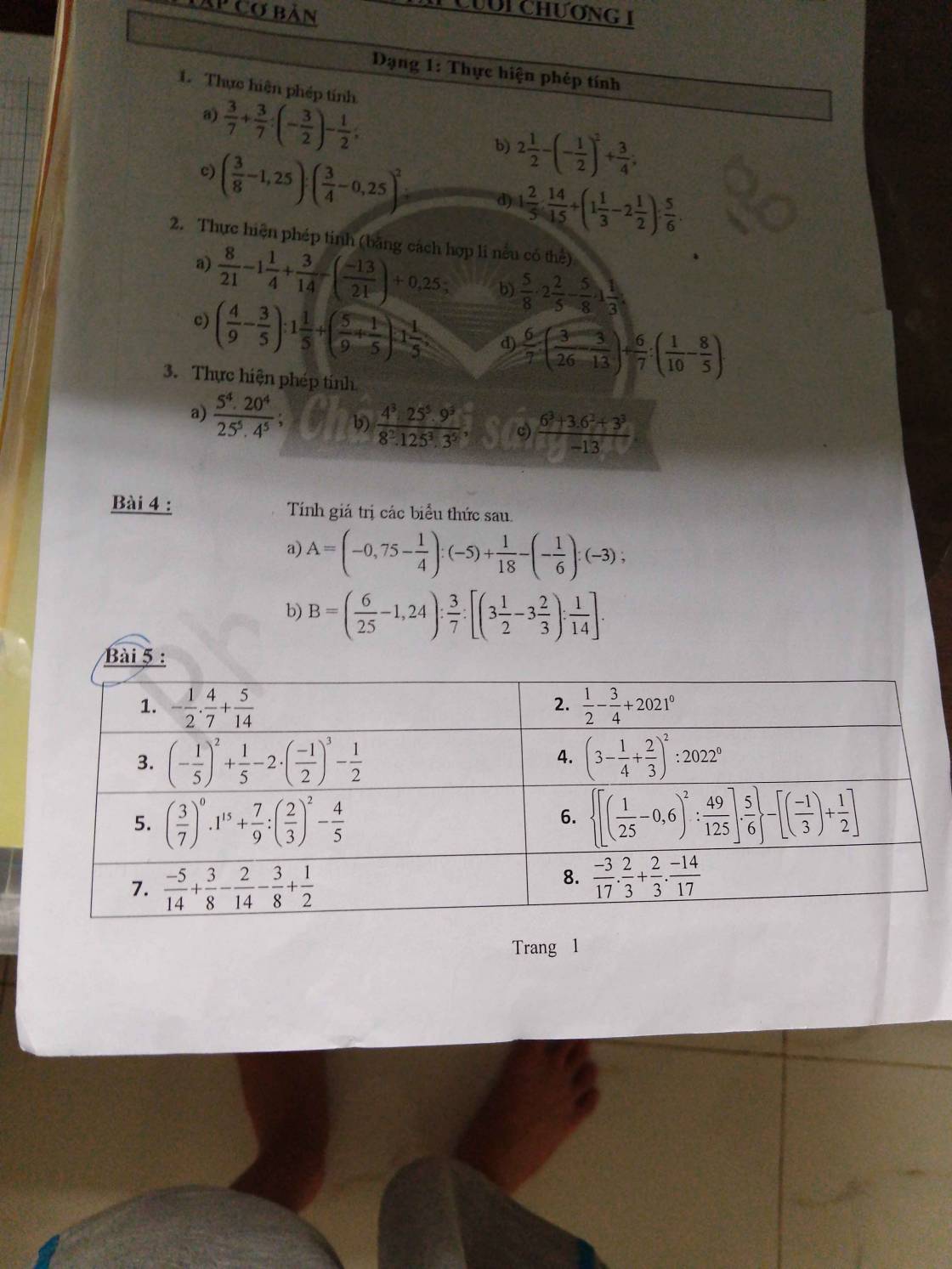
\(1,-\dfrac{1}{2}.\dfrac{4}{7}+\dfrac{5}{14}=-\dfrac{2}{7}+\dfrac{5}{14}\)

\(=\dfrac{1}{14}\)

\(2,\dfrac{1}{2}-\dfrac{3}{4}+2021^0=-\dfrac{1}{4}+1\)

\(=\dfrac{3}{4}\)

\(3,\left(-\dfrac{1}{5}\right)^2+\dfrac{1}{5}-2.\left(\dfrac{-1}{2}\right)^3-\dfrac{1}{2}\)

\(=\dfrac{1}{25}+\dfrac{1}{5}-2.\left(-\dfrac{1}{8}\right)-\dfrac{1}{2}\)

\(=\dfrac{6}{25}-\left(-\dfrac{1}{4}\right)-\dfrac{1}{2}=\dfrac{6}{25}+\dfrac{1}{4}-\dfrac{1}{2}\)

\(=\dfrac{49}{100}-\dfrac{1}{2}=-\dfrac{1}{100}\)

\(4,\left(3-\dfrac{1}{4}+\dfrac{2}{3}\right)^2:2022^0=\left(\dfrac{11}{4}+\dfrac{2}{3}\right)^2:1\)

\(=\dfrac{1681}{144}:1=\dfrac{1681}{144}\)

\(5,\left(\dfrac{3}{7}\right)^0.1^{15}+\dfrac{7}{9}:\left(\dfrac{2}{3}\right)^2-\dfrac{4}{5}\)

\(=1.1+\dfrac{7}{9}:\dfrac{4}{9}-\dfrac{4}{5}\)

\(=1+\dfrac{7}{9}.\dfrac{9}{4}-\dfrac{4}{5}=1+\dfrac{7}{4}-\dfrac{4}{5}\)

\(=\dfrac{11}{4}-\dfrac{4}{5}=\dfrac{39}{20}\)

\(6,\left\{\left[\left(\dfrac{1}{25}-0,6\right)^2:\dfrac{49}{125}\right].\dfrac{5}{6}\right\}-\left[\left(-\dfrac{1}{3}\right)+\dfrac{1}{2}\right]\)

\(=\left\{\left[\left(-\dfrac{14}{25}\right)^2.\dfrac{125}{49}\right].\dfrac{5}{6}\right\}-\dfrac{1}{6}\)

\(=\left[\left(\dfrac{196}{625}.\dfrac{125}{49}\right).\dfrac{5}{6}\right]-\dfrac{1}{6}\)

\(=\left(\dfrac{196.125}{625.49}.\dfrac{5}{6}\right)-\dfrac{1}{6}=\left(\dfrac{49.4.125}{5.125.49}.\dfrac{5}{6}\right)-\dfrac{1}{6}\)

\(=\left(\dfrac{4}{5}.\dfrac{5}{6}\right)-\dfrac{1}{6}=\dfrac{4}{6}-\dfrac{1}{6}=\dfrac{3}{6}=\dfrac{1}{2}\)

\(7,-\dfrac{5}{14}+\dfrac{3}{8}-\dfrac{2}{14}-\dfrac{3}{8}+\dfrac{1}{2}=\left(-\dfrac{5}{14}-\dfrac{2}{14}\right)+\left(\dfrac{3}{8}-\dfrac{3}{8}\right)+\dfrac{1}{2}\)

\(=-\dfrac{1}{2}+\dfrac{1}{2}=0\)

\(8,-\dfrac{3}{17}.\dfrac{2}{3}+\dfrac{2}{3}.\left(\dfrac{-14}{17}\right)=\dfrac{2}{3}.\left[-\dfrac{3}{17}+\left(-\dfrac{14}{17}\right)\right]\)

\(=\dfrac{2}{3}.\left(-1\right)=-\dfrac{2}{3}\)

#\(Cụt\)

#\(yGLinh\)

*Làm xong rồi ngỏm*

a, Xét ∆ ABH và ∆AHC có:

+AH chung

+ ∠AHB= ∠AHC(=90*)

+AB=AC(△ ABC cân)

=> △AHB=△AHC(ch-cgv)

=>BH=HC(2 cạnh tương ứng)

b) Xét △ HEB và △HFC có:

+ ∠BEH= ∠CFH(=90*)

+HB=HC(cmt)

+ ∠B= ∠C(△ABC cân)

=> △HEB=△HFC(ch-cgnhon)

`!`

\(-\dfrac{3}{4}+\dfrac{1}{2}:\dfrac{5}{6}\times\dfrac{10}{3}\\ =-\dfrac{3}{4}+\dfrac{1}{2}\times\dfrac{6}{5}\times\dfrac{10}{3}\\ =-\dfrac{3}{4}+\dfrac{6}{10}\times\dfrac{10}{3}\\ =-\dfrac{3}{4}+\dfrac{3}{5}\times\dfrac{10}{3}\\ =-\dfrac{3}{4}+\dfrac{30}{15}\\ =-\dfrac{3}{4}+2\\ =-\dfrac{3}{4}+\dfrac{8}{4}\\ =\dfrac{5}{4}\)

  \(\dfrac{3}{4}\) \(\times\) \(\dfrac{5}{9}\) + \(\dfrac{6}{7}\) : \(\dfrac{4}{3}\) - (\(\dfrac{7}{5}\) : \(\dfrac{4}{3}\))

= \(\dfrac{5}{12}\) + \(\dfrac{9}{14}\) - \(\dfrac{21}{20}\)

= \(\dfrac{175}{420}\) + \(\dfrac{270}{420}\) - \(\dfrac{441}{420}\)

= \(\dfrac{4}{420}\)

= \(\dfrac{1}{105}\)

5/12 + 9/14 - 21/20
= 1/105

Có phải là tìm \(x\); y nguyên không em? 

Ta có OH\(\perp\)AB 

=>OH là đường cao

Mà HC là đường cao của ∆OAB

=>∆OAB là ∆ cân

=> Oh cũng là đường trung trực của AB 

=> HA=HB (1)

Xét ∆OAB có: OA=OB (2)

Từ (1) và (2) =>HA=HB; OA=OB(đpcm)

b, Ta có HA=HB(cmt) 

=>HC là trung tuyến của ∆ABC

Mà ∆ ABC là ∆ đều

=>HC là đường trung trực của AB(2)

Từ (1);(2)=> O;H;C thẳng hàng (đpcm)