Tìm \(n\) ϵ \(Z\) để \(\dfrac{6n-1}{3n-2}\) có giá trị nhỏ nhất?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 61:
a, 5,5 : \(\dfrac{1}{2}\) = \(\dfrac{55}{10}\) : \(\dfrac{1}{2}\) = \(\dfrac{11}{1}\)
Vậy 5,5 : \(\dfrac{1}{2}\) = \(\dfrac{11}{1}\)
b, 1\(\dfrac{5}{7}\): (-1\(\dfrac{3}{9}\)) = \(\dfrac{12}{7}\): (-\(\dfrac{4}{3}\)) = - \(\dfrac{9}{7}\) = \(\dfrac{-9}{7}\)
vậy 1\(\dfrac{5}{7}\) = \(\dfrac{-9}{7}\)
c, (-0,12) : 2\(\dfrac{3}{4}\) = - \(\dfrac{12}{100}\) : \(\dfrac{11}{4}\) = - \(\dfrac{12}{275}\) = \(\dfrac{-12}{275}\)
vậy (-0,12) : 2\(\dfrac{3}{4}\) = \(\dfrac{-12}{275}\)
d, (-2,5) : 3,5 = \(\dfrac{-25}{10}\) : \(\dfrac{35}{10}\) = \(\dfrac{-5}{7}\)
vậy -2,5 : 3,5 = \(\dfrac{-5}{7}\)
Bài 62: (-5) : 10 = - \(\dfrac{1}{2}\); \(\dfrac{2}{5}\) : \(\dfrac{9}{7}\) = \(\dfrac{14}{45}\);
(-3,11) : 12,5 = - \(\dfrac{311}{1250}\); - \(\dfrac{14}{5}\) : 9 = - \(\dfrac{14}{45}\)
(-1,5): 3 = \(-\dfrac{1}{2}\); - \(\dfrac{311}{50}\): 25 = - \(\dfrac{311}{1250}\)
\(\dfrac{-5}{10}\) = \(\dfrac{-1,5}{3}\); \(\dfrac{-3,11}{12,5}\) = \(\dfrac{\dfrac{-311}{50}}{25}\)

\(2^{91}=\left(2^{13}\right)^7=73728^7\)
\(5^{35}=\left(5^5\right)^7=3125^7\) nhỏ hơn \(73728^7\)
\(\Rightarrow2^{91}\) lớn hơn \(5^{35}\)
\(b,3^{400}=\left(3^4\right)^{100}=81^{100}\\ 4^{300}=\left(4^3\right)^{100}=64^{100}\\ Vì:81^{100}>64^{100}\left(Do:81>64\right)\\ \Rightarrow3^{400}>4^{300}\)

\(\left(x+\dfrac{1}{3}\right)^2=\dfrac{1}{25}\\ \Rightarrow\left(x+\dfrac{1}{3}\right)^2=\left(\pm\dfrac{1}{5}\right)^2\\ \Rightarrow\left[{}\begin{matrix}x+\dfrac{1}{3}=\dfrac{1}{5}\\x+\dfrac{1}{3}=-\dfrac{1}{5}\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=-\dfrac{2}{15}\\x=-\dfrac{8}{15}\end{matrix}\right.\)
\(\left(x+\dfrac{1}{3}\right)^2=\dfrac{1}{25}\\ \Leftrightarrow\left[{}\begin{matrix}x+\dfrac{1}{3}=\dfrac{1}{5}\\x+\dfrac{1}{3}=-\dfrac{1}{5}\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{2}{15}\\x=-\dfrac{8}{15}\end{matrix}\right.\)
Vậy phương trình có nghiệm \(S=\left\{-\dfrac{2}{15};-\dfrac{8}{15}\right\}\)

\(\left(x-\dfrac{3}{4}\right)^2=\dfrac{1}{16}\\ \Rightarrow\left(x-\dfrac{3}{4}\right)^2=\left(\pm\dfrac{1}{4}\right)^2\\ \Rightarrow\left[{}\begin{matrix}x-\dfrac{3}{4}=\dfrac{1}{4}\\x-\dfrac{3}{4}=-\dfrac{1}{4}\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{1}{2}\end{matrix}\right.\)
(x-3/4)2=1/16=(1/4)2
=>x-3/4=1/4 hoặc x-3/4=-1/4
=>x=1/4+3/4=1 hoặc x=-1/4+3/4=2/4=1/2

\(\left(2x-3\right)^2=\dfrac{4}{25}\\ \Rightarrow\left(2x-3\right)^2=\left(\pm\dfrac{2}{5}\right)^2\\ \Rightarrow\left[{}\begin{matrix}2x-3=\dfrac{2}{5}\\2x-3=-\dfrac{2}{5}\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}2x=\dfrac{17}{5}\\2x=\dfrac{13}{5}\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{17}{10}\\x=\dfrac{13}{10}\end{matrix}\right.\)
\(\left(2x-3\right)^2=\dfrac{4}{25}\\ \Leftrightarrow\left(2x-3\right)^2=\left(\dfrac{2}{5}\right)^2\\ \Leftrightarrow\left[{}\begin{matrix}2x-3=\dfrac{2}{5}\\-2x+3=\dfrac{2}{5}\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{17}{5}\\-2x=-\dfrac{13}{5}\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{17}{10}\\x=\dfrac{13}{10}\end{matrix}\right.\)
Vậy...

Lời giải:
Gọi số bộ quần áo 2 phân xưởng may được lần lượt là $a,b$ (bộ)
Theo bài ra ta có:
$a+b=1125$
$a:b=0,8=4:5$
$\Rightarrow \frac{a}{4}=\frac{b}{5}=\frac{a+b}{4+5}=\frac{1125}{9}=125$ (áp dụng tính chất dtsbn)
$\Rightarrow a=125.4=500; b=125.5=625$ (bộ)

a,x.y=3=1x3=3x1=-1x(-3)=-3x(-1).
Vậy (x,y)=(1,3)=(3,1)=(-1,-3)=(-3,-1)
b,x.(y+1)=5=1x5=5x1=-1x(-5)=-5x(-1)
=>
| x | 1 | 5 | -1 | -5 |
| y+1 | 5 | 1 | -5 | -1 |
| y | 4 | 0 | -6 | -2 |
Vậy (x,y)=(1,4)=(5,0)=(-1,-6)=(-1,-2).
c,(x-2)(y+3)=7=1x7=7x1=-1x(-7)=-7(-1)
=>
| x-2 | 1 | 7 | -1 | -7 |
| y+3 | 7 | 1 | -7 | -1 |
| x | 3 | 9 | 1 | -5 |
| y | 4 | -2 | -10 | -4 |
Vậy (x,y)=(3,4)=(9,-2)=(1,-10)=(-5,-4).

Lời giải:
a. $3(x-\frac{1}{2})-3(x-\frac{1}{3})=x$
$3[(x-\frac{1}{2})-(x-\frac{1}{3})]=x$
$3.\frac{-1}{6}=x$
$\Rightarrow x=\frac{-1}{2}$
b.
$\frac{1}{2}(x+2)-4(x-\frac{1}{4})=\frac{1}{2}x$
$\frac{1}{2}x+1-4(x-\frac{1}{4})=\frac{1}{2}x$
$1-4(x-\frac{1}{4})=0$
$x-\frac{1}{4}=\frac{1}{4}$
$x=\frac{1}{4}+\frac{1}{4}=\frac{1}{2}$
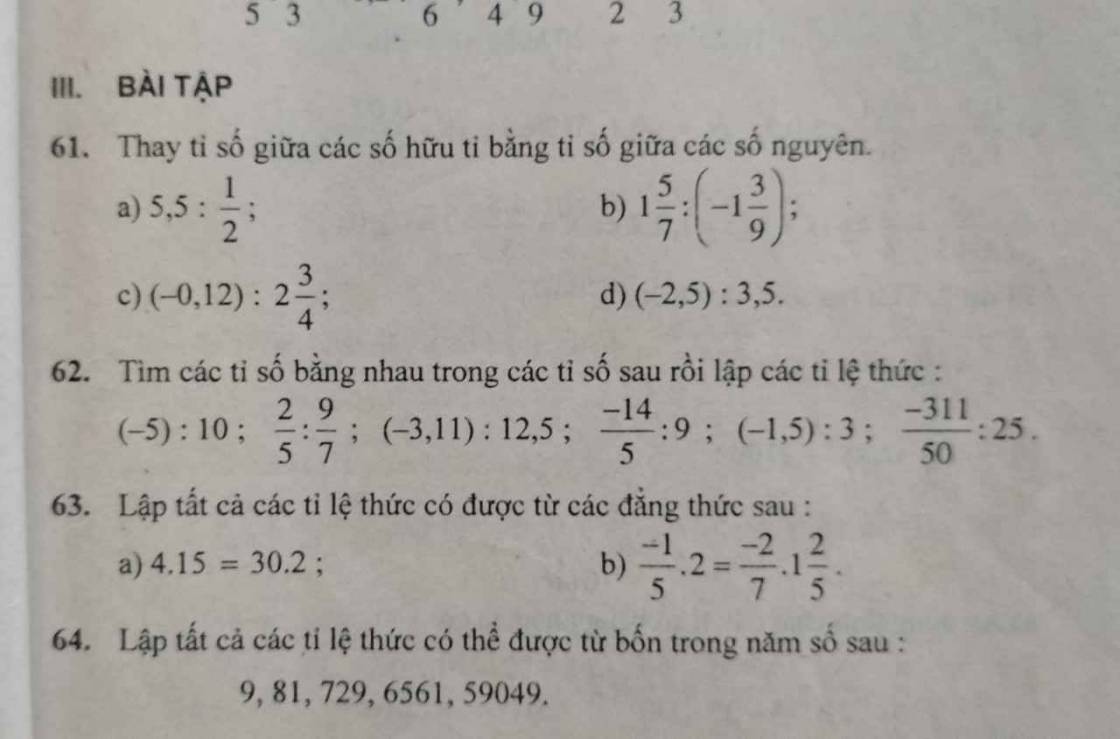

\(A=\dfrac{6n-1}{3n-2}\)
\(\Rightarrow A=\dfrac{6n-4+3}{3n-2}\)
\(\Rightarrow A=\dfrac{2\left(3n-2\right)+3}{3n-2}\)
\(\Rightarrow A=2+\dfrac{3}{3n-2}\ge2+\dfrac{3}{3.1-2}=5\left(n=1\in Z\right)\)
\(\Rightarrow Min\left(A\right)=5\left(n=1\right)\)
mkmhkkkkkkkkkkkkkk