tim mot so biet rang so do co 500 qua trung
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CH
Cô Hoàng Huyền
Admin
VIP
28 tháng 3 2018
a) Xét tam giác vuông OAD và tam giác vuông OBE có:
Góc O chung
OA = OB
\(\Rightarrow\Delta OAD=\Delta OBE\) (Cạnh huyền - góc nhọn)
\(\Rightarrow OE=OD\)
\(\Rightarrow\frac{OE}{OA}=\frac{OD}{OB}\Rightarrow ED//AB\) (Định lý Talet đảo)
b) Ta có ngay \(\Delta OEB\sim\Delta OAC\left(g-g\right)\Rightarrow\frac{OE}{OA}=\frac{OB}{OC}\)
\(\Rightarrow OA.OB=OE.OC\Rightarrow OB^2=OE.OC\)
c) Ta cũng có ngay \(\Delta AEB=\Delta BDA\) (Cạnh huyền - góc nhọn)
\(\Rightarrow\widehat{DAB}=\widehat{EBA}\)
Lại có \(\widehat{EBA}=\widehat{BAC}\) (Hai góc so le trong)
Nên \(\widehat{DAB}=\widehat{BAC}\) hay AB là phân giác góc CAD.
d) Ta có EB // AC nên áp dụng Ta let thì:
\(\frac{OE}{AE}=\frac{OB}{BC}\Rightarrow OE.BC=OB.AE\)
Mà OB = OA, AE = BD
Vậy nên \(OE.BC=OA.BD\)
CH
Cô Hoàng Huyền
Admin
VIP
27 tháng 3 2018
Gọi J là trung điểm BC. Khi đó AJ là trung tuyến. Vậy thì AG = 2GJ. (1)
Xét tứ giác BIKC có BI cùng CK cùng song song với AG nên BI // CK hay BIKC là hình thang.
Xét hình thang BIKC có :
J là trung điểm BC
GJ // BI // KC
Suy ra GJ là đường trung bình hình thang BIKC.
Từ đó ta có: \(BI+CK=2GJ\) (2)
Từ (1) và (2) suy ra \(BI+KC=AG\)
CH
Cô Hoàng Huyền
Admin
VIP
22 tháng 3 2018
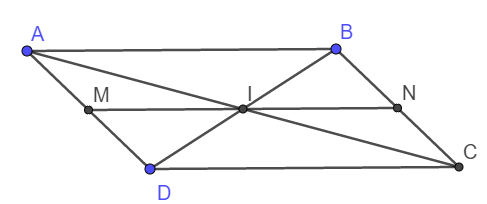
1. Xét tam giác ABD có MI // AB nên theo định lý Talet ta có:
\(\frac{MI}{AB}=\frac{DI}{DB}\)
Xét tam giác ABC có NI // AB nên theo định lý Talet ta có:
\(\frac{NI}{AB}=\frac{NC}{BC}\)
2. Xét tam giác BDC có IN // DC nên \(\frac{DI}{DB}=\frac{NC}{BC}\)
Từ đó ta có: \(\frac{MI}{AB}=\frac{NI}{AB}\Rightarrow MI=IN\)
Vậy I là trung điểm MN (đpcm)
16 tháng 3 2018
ọi phương trình là A
A <=> 4x^6 + 4x^5 + 4x^4 + 4x^3 + 4x^2 + 4x + 3 + 1 = 0
<=> (4x^6 + 4x^5 + x^4) + (2x^4 + 4x^3 + 2x^2) + (2x^2 + 4x + 2) + x^4 + 2 = 0
<=> [2.(2x^3 + x^2)^2 + 2.(√2.x^2 + √2 . x)^2 + 2.(x+1)^2 + x^4] + 2 = 0
Xét tổng các số hạng trong ngoặc vuông, các số hạng đều có thừa số 2>0, thừa số còn lại là bình phương của 1 số sẽ > 0, còn số hạng ngoài ngoặc (số 2) hiển nhiên > 0. Từ đây suy ra phương trình A vô nghiệm.
Còn cách nữa chứng minh phương trình trên vô nghiệm. Nhân cả 2 vế với x-1 rồi thu gọn, ta có phương trình: x^7 - 1 = 0 <=> x = 1.
Ta thấy x = 1 không là nghiệm của phương trình A, vậy ta có phương trình A vô nghiệm.
(Bài tính thì theo bài của bạn, còn phần chứng minh năm ở bài 290, sách Nâng cao và phát triển toán 8 tập 2, trang 15)
P/S: Đình Huy ơi, chỗ (x + 1/x)^3 - 3.x.1/x.(x + 1/x) hình như phải là (x + 1/x)^3 - 3.x.1/x.(x - 1/x) chứ nhỉ?
KT
16 tháng 3 2018
cách đơn giản hơn nhé.
Đặt \(A=x^6+x^5+x^4+x^3+x^2+x+1=0\)
\(\Leftrightarrow\)\(x^5\left(x+1\right)+x^3\left(x+1\right)+x\left(x+1\right)+1=0\)
\(\Leftrightarrow\)\(\left(x+1\right)\left(x^5+x^3+x\right)+1=0\)
\(\Leftrightarrow\)\(x\left(x+1\right)\left(x^4+x^2+1\right)+1=0\)
Ta có: \(x^4+x^2+1=\left(x^2+\frac{1}{2}\right)+\frac{3}{4}>0\) \(\forall x\)
Nếu \(x\ge0\)thì \(x+1>0\)\(\Rightarrow\)\(x\left(x+1\right)\left(x^4+x^2+1\right)\ge0\)\(\Rightarrow\)\(A>1\)
Nếu \(x=-1\) thì \(x+1=0\)\(\Rightarrow\) \(A=1\)
Nếu \(x< -1\) thì \(x+1< 0\) \(\Rightarrow\) \(A>0\)
Vậy pt vô nghiệm
P/s: sai đâu m.n chỉ cho mk nhé
10500
10500