một khu vườn hình chữ nhật có chiều dài dài hơn chiều rộng 8m nếu tăng chiều dài 10m và giảm chiều rộng 4m thì diện tích khu vườn không thay đổi tính kích thước ban đầu khu vườn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi chiều dài của khu vườn là a (a > 0,m), khi đó chiều rộng của khu vườn là a - 8 m
Khi đó diện tích của khu vườn là a(a - 8) m2
Vì khi tăng chiều dài của khu vườn thêm 10m, giảm chiều rộng của khu vườn đi 4m thì diện tích không thay đổi.
=> Ta có a(a - 8) = (a + 10)(a - 12)
<=> a^2 - 8a = a^2 - 2a - 120
<=> 6a - 120 = 0 <=> a = 20
Vậy...

Câu 1:
a) 2x(3x+2) - 3x(2x+3) = 6x^2+4x - 6x^2-9x = -5x
b) \(\left(x+2\right)^3+\left(x-3\right)^2-x^2\left(x+5\right)\)
\(=x^3+6x^2+12x+8+x^2-6x+9-x^3-5x^2\)
\(=2x^2+6x+17\)
c) \(\left(3x^3-4x^2+6x\right)\div\left(3x\right)=x^2-\dfrac{4}{3}x+2\)

Gọi tuổi của bạn là `x`
Lấy tuổi đó cộg thêm `5`, được bao nhiêu đem nhân với `2`, lấy kq trên cộg với `10` r nhân kq vừa tìm được với `5` sau đó trừ `100` ta có biểu thức:
`[(x+5).2+10].5-100`
`=10(x+5)+50-100`
`=10x+50+50-100`
`=10x`
Ta thấy được kq của biểu thức trên bằng` 10` lần số tuổi thực của bạn, nên ta chỉ cần lấy kết quả cuối cùng chia cho `10` thì ra tuổi thực

a/ Xét tg DIE và tg CID có
\(\widehat{CDE}=\widehat{BCD}\) (góc so le trong)
\(\widehat{BED}=\widehat{CBE}\) (góc so le trong)
=> tg DIE đồng dạng tg CID (g.g.g)
b/
Ta có DE//BC
Xét tg ABM có \(\dfrac{DN}{BM}=\dfrac{AN}{AM}\) (1)
Xét tg ACM có \(\dfrac{EN}{CM}=\dfrac{AN}{AM}\) (2)
Từ (1) và (2) \(\Rightarrow\dfrac{DN}{BM}=\dfrac{EN}{CM}\) mà BM=CM => DN=EN
c/
Nôi A với I cắt DE tại N'; cắt BC tại M'
Ta có
\(\dfrac{DN'}{CM'}=\dfrac{IN'}{IM'}\)
\(\dfrac{EN'}{BM'}=\dfrac{IN'}{IM'}\)
\(\Rightarrow\dfrac{DN'}{CM'}=\dfrac{EN'}{BM'}\) (1)
Ta có
\(\dfrac{EN'}{CM'}=\dfrac{AI}{AM'}\)
\(\dfrac{DN'}{BM'}=\dfrac{AI}{AM'}\)
\(\Rightarrow\dfrac{EN'}{CM'}=\dfrac{DN'}{BM'}\) (2)
Công 2 vế của (1) và (2)
\(\dfrac{DN'+EN'}{CM'}=\dfrac{EN'+DN'}{BM'}\Rightarrow\dfrac{DE}{CM'}=\dfrac{DE}{BM'}\)
=> CM' = BM' => M' là trung điểm của BC => M trùng M'
Từ (1) => DN'=EN' => N' là trung điểm của DE mà N là trung điểm của DE => N trùng N'
=> N; I; M thẳng hàng

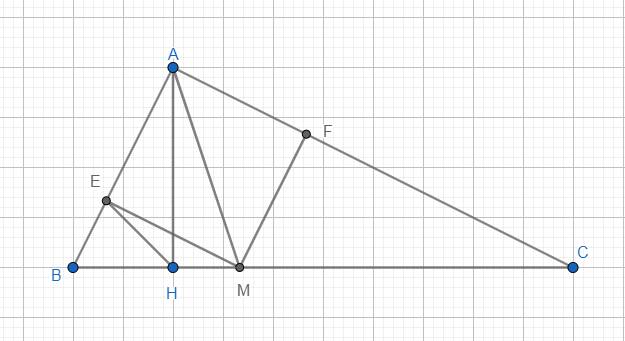
a) Xét △BEM và △BHA có:
\(\hat{B}\): chung
\(\hat{BEM}=\hat{BHA}\) = 90o
Do đó: △BEM đồng dạng △BHA (gg)
=> \(\dfrac{BE}{BH}=\dfrac{BM}{BA}\) => BE.BA = BH.BM
b) Theo câu a), ta có:
BE.BA = BH.BM
=> \(\dfrac{BE}{BM}=\dfrac{BH}{BA}\)
Lại có: \(\hat{B}\): chung
nên △BEH đồng dạng △BMA (cgc)
=> \(\hat{BHE}=\hat{BAM}\)
Vì AM là tia phân giác của \(\hat{BAC}\) nên \(\hat{BAM}=\dfrac{\hat{BAC}}{2}=\dfrac{90^o}{2}=45^0\)
=> \(\hat{BHE}=45^0\)
mà \(\hat{BHA}=90^o\)
Nên HE là tia phân giác góc AHB.
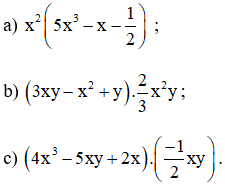

Gọi chiều dài ban đầu là \(x\left(m\right)\) thì chiều rộng ban đầu là \(x-8\left(m\right)\)
Chiều dài sau khi thay đổi là \(x+10\left(m\right)\), chiều rộng sau khi thay đổi là \(x-8-4=x-12\left(m\right)\)
Ta có: \(x\left(x-8\right)=\left(x+10\right)\left(x-12\right)\)
\(\Rightarrow x^2-8x=x^2-12x+10x-120\)
\(\Rightarrow6x=120\Rightarrow x=20\left(m\right)\)
Vậy chiều dài ban đầu là 20m, chiều rộng ban đầu là 12m.