Tìm 2 số tự nhiên liên tiếp biết hiệu bình phương chúng là 56
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a/
Ta có
\(BC=\sqrt{AB^2+AC^2}\) (Pitago)
\(\Rightarrow BC=\sqrt{15^2+20^2}=25cm\)
\(\dfrac{AD}{AB}=\dfrac{CD}{BC}\) (Trong tg đường phân giác của 1 góc chia cạnh đối diện thành 2 đoạn thẳng tỷ lệ với 2 cạnh kề hai đoạn thẳng đó)
\(\Rightarrow\dfrac{AD}{AB}=\dfrac{CD}{BC}=\dfrac{AD+CD}{AB+BC}=\dfrac{AC}{AB+BC}=\dfrac{20}{15+25}=\dfrac{1}{2}\)
\(\Rightarrow AD=\dfrac{AB}{2}=\dfrac{15}{2}=7,5cm\)
b/
Ta có
\(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{15^2}{25}=9cm\)
Xét tg vuông ABH có
\(AH=\sqrt{AB^2-BH^2}=\sqrt{15^2-9^2}=12cm\)
c/
Xét tg vuông ABD có
\(\widehat{ABD}+\widehat{ADB}=90^o\)
Xét tg vuông BIH có
\(\widehat{CBD}+\widehat{BIH}=90^o\)
Mà \(\widehat{ABD}=\widehat{CBD}\) (Do BD là phân giác \(\widehat{ABC}\) )
\(\Rightarrow\widehat{ADB}=\widehat{BIH}\)
Mà \(\widehat{BIH}=\widehat{AID}\) (góc đối đỉnh)
\(\Rightarrow\widehat{ADB}=\widehat{AID}\) => tg AID cân tại A

\(A=\left(\dfrac{x^2}{x^3-4x}+\dfrac{6}{6-3x}+\dfrac{1}{x+2}\right):\left(x-2+\dfrac{10-x^2}{x+2}\right)\)
\(ĐK:x\ne0;2;-2\)
\(A=\left(\dfrac{x^2}{x\left(x^2-4\right)}+\dfrac{6}{3\left(2-x\right)}+\dfrac{1}{x+2}\right):\left(\dfrac{\left(x-2\right)\left(x+2\right)+10-x^2}{x+2}\right)\)
\(A=\left(\dfrac{x}{x^2-4}+\dfrac{2}{2-x}+\dfrac{1}{x+2}\right):\left(\dfrac{x^2-4+10-x^2}{x+2}\right)\)
\(A=\left(\dfrac{x-2\left(x+2\right)+\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\right):\left(\dfrac{6}{x+2}\right)\)
\(A=\dfrac{x-2x-4+x-2}{\left(x-2\right)\left(x+2\right)}.\dfrac{x+2}{6}\)
\(A=\dfrac{-6}{\left(x-2\right)\left(x+2\right)}.\dfrac{x+2}{6}\)
\(A=-\dfrac{1}{x-2}\)

`a)(2x-3y)(x-2y)`
`=2x^2-4xy-3xy+6y^2=2x^2-7xy+6^2`
`b)(3x+2)^2-(x-1)(2x-3)`
`=9x^2+12x+4-2x^2+3x+2x-3=7x^2+17x+1`
`c)(x-2)^2-3(x-3)(x+3)-(x-2)`
`=x^2-4x+4-3x^2+27-x+2`
`=-2x^2-5x+33`
`a)`\(\left(2x-3y\right)\left(x-2y\right)=2x^2-4xy-3xy+6y^2=2x^2-7xy+6y^2\)
`b)`\(\left(3x+2\right)^2-\left(x-1\right)\left(2x-3\right)=9x^2+12x+4-\left(2x^2-3x-2x+3\right)=7x^2+17x+1\)
`c)`
\(\left(x-2\right)^2-3\left(x-3\right)\left(x+3\right)-\left(x-2\right)=x^2-4x+4-3x^2+27-x+2=-2x^2-5x+33\)


\(\left(x-1\right)\left(x^2+x+1\right)-x\left(x+2\right)\left(x-2\right)=5\)
\(\Leftrightarrow x^3-1-x\left(x^2-4\right)=5\)
\(\Leftrightarrow x^3-1-x^3+4x=5\)
\(\Leftrightarrow4x=6\)
`<=>x=3/2`
Vậy \(S=\left\{\dfrac{3}{2}\right\}\)

`x^2-2x >= 0`
`<=>x(x-2) >= 0`
`<=>` $\left[\begin{matrix} \begin{cases} x \ge 0\\x-2 \ge 0 \end{cases}\\ \begin{cases} x \le 0\\x-2 \le 0 \end{cases}\end{matrix}\right.$
`<=>` $\left[\begin{matrix} \begin{cases} x \ge 0\\x \ge 2 \end{cases}\\ \begin{cases} x \le 0\\x \le 2 \end{cases}\end{matrix}\right.$
`<=>` $\left[\begin{matrix} x \ge 2\\ x \le 0\end{matrix}\right.$
Vậy `S={x|x >= 2;x <= 0}`
\(x^2-2x\ge0\Leftrightarrow x\left(x-2\right)\ge0\)
\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge0\\x-2\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}x< 0\\x-2< 0\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge0\\x\ge2\end{matrix}\right.\\\left\{{}\begin{matrix}x< 0\\x< 2\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x\ge2\\x< 0\end{matrix}\right.\)
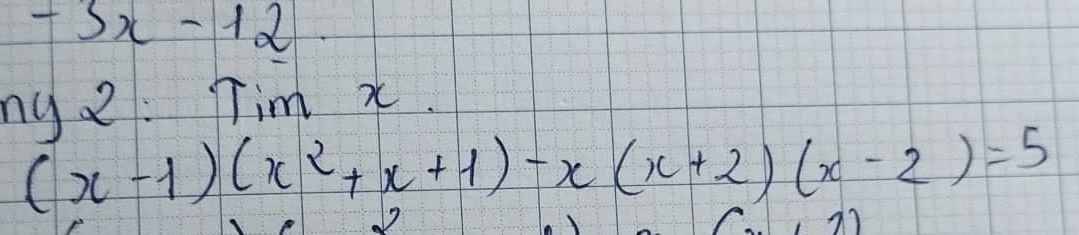
2 số tự nhiên liên tiếp có dạng
n và n + 1 trong đó n ϵ N*
theo bài ra ta có (n+1)2 - n2 = 56
⇔ (n+ 1 - n)(n+1+n) = 56
⇔ n + n + 1 = 56
2n = 56 -1
2n = 55 (vô lý vì 2n phải là số chẵn)
vậy không có 2 số tự nhiên nào thỏa mãn đề bài
Gọi số tự nhiên nhỏ hơn là x (ĐK: x ∈ N*) thì số tự nhiên lớn hơn là x + 1.
Biết hiệu bình phương của chúng là 56 nên ta có phương trình:
\(\left(x+1\right)^2-x^2=56\\ \Leftrightarrow x^2+2x+1-x^2=56\\ \Leftrightarrow2x=55\\ \Leftrightarrow x=\dfrac{55}{2}\left(ktmđk\right)\)
Bạn xem lại đề giúp mình nhé!