Thời gian ô tô đi từ A đến B là:

14 giờ 15 phút - 1 giờ 30 phút - 8 giờ 15 phút = 4 giờ 30 phút

Đổi: 4 giờ 30 phút = 4,5 giờ 

Vận tốc của ô tô là:

\(200:4,5=\dfrac{400}{9}\left(km/h\right)\)

ĐS: ... 

Đổi: 1,6m = 16dm, 0,8m = 8dm, 1,2m = 12dm 

Bể có thể chứa được số lít nước là: 

\(16\times8\times12=1536\left(dm^3\right)=1536\left(l\right)\)

ĐS: ... 

    [36,57 - 8,435] x 0,15: 0,01

 = 28,135 x 0,15: 0,01

= 28,135 x (0,15: 0,01)

= 28,135 x 15

= 422,025

b; 

   88,16 : [1,32 + 3,48] - 0,64

= 88,16 : 4,8 - 0,64

= \(\dfrac{551}{30}\) - \(\dfrac{16}{25}\)

= \(\dfrac{2659}{150}\)

13,04dm3 = 0,01304 m3

25 giờ 48 phút : 4 = 6 giờ 27 phút

25 giờ 48 phút : 4 = 6,45 giờ

a: Vì \(NQ=\dfrac{1}{3}NP\)

nên \(S_{MNQ}=\dfrac{1}{3}\cdot S_{MNP}\)

b: Ta có: NQ+QP=NP

=>\(QP=NP-NQ=NP-\dfrac{1}{3}NP=\dfrac{2}{3}NP\)

=>\(QN=\dfrac{1}{2}QP\)

=>\(S_{MNQ}=\dfrac{1}{2}\cdot S_{MQP}\)

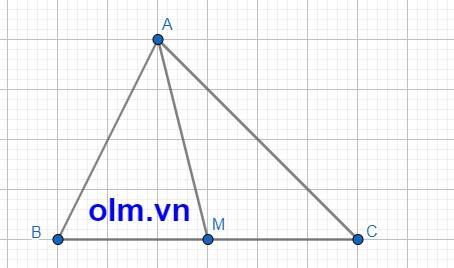
S_AMC  = \(\dfrac{1}{2}\) S_ABC vì hai tam giác có chung chiều cao và MC = \(\dfrac{1}{2}\) BC

S_ABC  = 2 x S_ABM (vì hai tam giác có chung chiều cao và BC = 2 x BM

Vì KC=1/2KA

nên \(AK=\dfrac{2}{3}AC\)

=>\(S_{ABK}=\dfrac{2}{3}\cdot S_{ABC}=170\left(cm^2\right)\)

Vì \(QB=\dfrac{3}{5}BA\) nên \(AQ=\dfrac{2}{5}AB\)

=>\(S_{AQK}=\dfrac{2}{5}\cdot S_{ABK}=\dfrac{2}{5}\cdot170=68\left(cm^2\right)\)

ta có: \(S_{AQK}+S_{BQKC}=S_{ABC}\)

=>\(S_{BQKC}+68=255\)

=>\(S_{BQKC}=255-68=187\left(cm^2\right)\)

Diện tích cần quét xi măng là:

\(2\times1,5+\left(2+1,5\right)\times2\times2=17\left(m^2\right)\)

Để quét sơn hết bể thì mất:

\(17:1\times14=238\left(p\right)\)

ĐS: ... 

0,5 ngày = 12 giờ

0,5 ngày = 24 giờ x 0,5  = 12 giờ