\(\sqrt{10+4\sqrt{ }6}-\sqrt{10-4\sqrt{ }6}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
N
8 tháng 6 2022
a) x2 - 2x + y2 + 1 = 0
<=> (x - 1)2 + y2 = 0
<=> x - 1 = 0 và y = 0 <=> x = 1 và y = 0
Vậy S = {(1; 0)}
b) -2x2 + 4x - y2 - 2y - 3 = 0
<=> -2(x - 1)2 - (y - 1)2 = 0
<=> 2(x - 1)2 + (y - 1)2 = 0
<=> x - 1 = 0 và y - 1 = 0 <=> x = 1 và y = 1
Vậy S = {(1; 1)}
c) x2 + 2y2 - 2xy + 2x - 6y + 5 = 0
<=> (x - y)2 + 2(x - y) + 1 + (y - 2)2 = 0
<=> (x - y + 1)2 + (Y - 2)2 = 0
<=> x - y + 1 = 0 và y - 2 = 0
<=> y = 2 và x = -1
Vậy S = {(-1 ; 2)}
ND
0
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
6 tháng 6 2022
(x + a )(x +b) = x2 + (a +b) x +ab
(x + a )(x +b) = x2 + bx + ax + ab
= x2 + (a +b)x + ab (đcm)
(x + a )(x +b)(x + c) = ( x2 + (a +b)x + ab)(x +c)
= x3 + cx2 + (a+b)x2 + (a+b)cx +abx+abc
= x3 + (a+b+c) x2 + [ (a+b)c +ab] x +abc
= x3 + (a + b +c ) x2 + (ab +bc +ac) x + abc (đpcm)
YN
19 tháng 6 2022
\(\left(3+1\right)\left(3^2+1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)\left(3^{32}+1\right)\)
\(=1\left(3+1\right)\left(3^2+1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)\left(3^{32}+1\right)\)
\(=\dfrac{3-1}{2}\left(3+1\right)\left(3^2+1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)\left(3^{32}+1\right)\)
\(=\dfrac{1}{2}\left(3-1\right)\left(3+1\right)\left(3^2+1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)\left(3^{32}+1\right)\)
\(=\dfrac{1}{2}\left(3^4-1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)\left(3^{32}+1\right)\)
\(=\dfrac{1}{2}\left(3^8-1\right)\left(3^8+1\right)\left(3^{16}+1\right)\left(3^{32}+1\right)\)
\(=\dfrac{1}{2}\left(3^{16}-1\right)\left(3^{16}+1\right)\left(3^{32}+1\right)\)
\(=\dfrac{1}{2}\left(3^{32}-1\right)\left(3^{32}+1\right)\)
\(=\dfrac{3^{64}-1}{2}\)
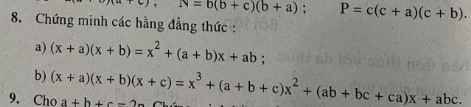
`\sqrt{10+4\sqrt{6}}-\sqrt{10-4\sqrt{6}}`
`=\sqrt{2^2+2.2.\sqrt{6}+6}-\sqrt{2^2-2.2.\sqrt{6}+6}`
`=\sqrt{(2+\sqrt{6})^2}-\sqrt{(2-\sqrt{6})^2}`
`=|2+\sqrt{6}|-|2-\sqrt{6}|`
`=2+\sqrt{6}-\sqrt{6}+2=4`
\(\sqrt{10+4\sqrt{6}}-\sqrt{10-4\sqrt{6}}=\sqrt{\left(2+\sqrt{6}\right)^2}-\sqrt{\left(2-\sqrt{6}\right)^2}=2+\sqrt{6}-\sqrt{6}+2=4\)