Qiqi đi bộ từ thư viện đến trường với vận tốc 60m/phút. Hai phút sau đó, Weiling cũng rời thư viện đến trường với vận tốc 72m/phút. Weiling đến trường trước qiqi 4 phút. Hỏi quãng đường từ thư viện đến trường dài bao nhiêu mét? giải thích hộ mình nhé. mình cảm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(3x^3-14x^2+4x+3\)
\(=3x^3+x^2-15x^2-5x+9x+3\)
\(=x^2\left(3x+1\right)-5x\left(3x+1\right)+3\left(3x+1\right)\)
\(=\left(3x+1\right)\left(x^2-5x+3\right)\)

Gọi hai số cần tìm là a,b
Theo đề, ta có: \(\dfrac{a}{b}=\dfrac{7}{12}\)
=>\(\dfrac{a}{7}=\dfrac{b}{12}\)
=>12a=7b
=>12a-7b=0(1)
Thêm 10 đơn vị vào số thứ nhất thì tỉ số giữa chúng là 3/4 nên \(\dfrac{a+10}{b}=\dfrac{3}{4}\)
=>4(a+10)=3b
=>4a+40=3b
=>4a-3b=-40(2)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}12a-7b=0\\4a-3b=-40\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}12a-7b=0\\12a-9b=-120\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}12a-7b-12a+9b=0-\left(-120\right)\\12a=7b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=60\\12a=7\cdot60=420\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=35\\b=60\end{matrix}\right.\)
Tổng của hai số là 35+60=95

+, Với \(a=0;b\ne c\ne0\), khi đó:
\(0^2=b^5-b^4c\)
\(\Rightarrow b^4\left(b-c\right)=0\)
\(\Rightarrow b-c=0\) (vì \(b\ne0\))
\(\Rightarrow b=c\) (loại)
+, Với \(b=0;a\ne c\ne0\), khi đó:
\(a^2=0^5-0^4.c\)
\(\Rightarrow a^2=0\Rightarrow a=0\) (loại)
+, Với \(c=0;a\ne b\ne0\), khi đó:
\(a^2=b^5-b^4.0\)
\(\Rightarrow a^2=b^5\)
Mà trong ba số a, b, c có 1 số dương, 1 số âm và 1 số bằng 0 nên ta có các TH sau:
*) Nếu \(a>0;b< 0\) thì:
\(a^2>0;b^5< 0\Rightarrow a^2\ne b^5\) (loại)
*) Nếu \(a< 0;b>0\Rightarrow a^2>0;b^5>0\) (tm)
Vậy số 0 là c; số dương là b; số âm là a.

ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC=\sqrt{BC^2-AB^2}=5\left(cm\right)\)
Xét ΔABC vuông tại A có
\(sinB=cosC=\dfrac{AC}{BC}=\dfrac{5}{5\sqrt{2}}=\dfrac{1}{\sqrt{2}}\)
\(cosB=sinC=\dfrac{AB}{BC}=\dfrac{5}{5\sqrt{2}}=\dfrac{1}{\sqrt{2}}\)
\(tanB=cotC=\dfrac{AC}{AB}=\dfrac{5}{5}=1\)
\(cotB=tanC=\dfrac{AB}{AC}=\dfrac{5}{5}=1\)
Theo Pytago tam giac ABC vuong tai A
\(AC=\sqrt{BC^2-AB^2}=\sqrt{50-25}=5\)
Do ^B; ^C phu nhau
sinB = AC/BC = 1/can2 = cosC
cosB = AB/BC = 1/can2 = sinC
tanB = AC/AB = 1 = cotC
cotB = AC/AB = 1 = tanC

a: \(BN=\dfrac{1}{3}BC\)
=>\(BN=\dfrac{1}{2}CN\)
=>\(S_{NBO}=\dfrac{1}{2}S_{CNO}\)
=>\(S_{CNO}=2\times S_{NBO}=240\left(cm^2\right)\)
b: Vì M,N,O thẳng hàng
nên \(\dfrac{MA}{MC}\times\dfrac{NC}{NB}\times\dfrac{OB}{OA}=1\)
=>\(\dfrac{OB}{OA}\times2=1\)
=>\(\dfrac{OB}{OA}=\dfrac{1}{2}\)
=>B là trung điểm của OA
=>\(\dfrac{S_{NBO}}{S_{NBA}}=\dfrac{OB}{BA}=1\)
=>\(S_{NBA}=S_{NBO}=\dfrac{1}{2}S_{CNO}\)
Vì B là trung điểm của OA
nên OA=2OB
=>\(S_{ANO}=2\times S_{NBO}=S_{CNO}\)
c: Vì \(S_{NBA}=S_{NBO}\)
nên \(S_{NBA}=120\left(cm^2\right)\)
Vì BN/BC=1/3
nên BC=3BN
=>\(S_{ABC}=3\times S_{ABN}=360\left(cm^2\right)\)

Đặt \(A=1+2+2^2+...+2^{2011}\)
=>\(2A=2+2^2+...+2^{2012}\)
=>\(2A-A=2+2^2+...+2^{2012}-1-2-...-2^{2011}\)
=>\(A=2^{2012}-1\)
\(D=2^{2012}-A=2^{2012}-2^{2012}+1=1\)

a: \(AE=\dfrac{1}{2}EC\)
=>\(\dfrac{AE}{AC}=\dfrac{1}{3}\)
Vì EF//AB
nên \(\dfrac{BF}{BC}=\dfrac{AE}{AC}\)
=>\(\dfrac{BF}{BC}=\dfrac{1}{3}\)
=>\(S_{AFB}=\dfrac{1}{3}\times S_{ABC}\)
ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\times AB\times AC=\dfrac{1}{2}\times12\times18=108\left(cm^2\right)\)
=>\(S_{AFB}=\dfrac{108}{3}=36\left(cm^2\right)\)
b: Vì EF//AB
nên \(\dfrac{EF}{AB}=\dfrac{CE}{CA}=\dfrac{2}{3}\)
=>\(\dfrac{EF}{12}=\dfrac{2}{3}\)
=>EF=8(cm)

\(\dfrac{4x^2+16}{x^2+6}=\dfrac{3}{x^2+1}+\dfrac{5}{x^2+3}+\dfrac{7}{x^2+5}\)
=>\(\dfrac{4x^2+16}{x^2+6}-3=\dfrac{3}{x^2+1}-1+\dfrac{5}{x^2+3}-1+\dfrac{7}{x^2+5}-1\)
=>\(\dfrac{x^2-2}{x^2+6}=\dfrac{-x^2+2}{x^2+1}+\dfrac{-x^2+2}{x^2+3}+\dfrac{-x^2+2}{x^2+5}\)
=>\(\dfrac{x^2-2}{x^2+6}+\dfrac{x^2-2}{x^2+1}+\dfrac{x^2-2}{x^2+3}+\dfrac{x^2-2}{x^2+5}=0\)
=>\(\left(x^2-2\right)\left(\dfrac{1}{x^2+6}+\dfrac{1}{x^2+1}+\dfrac{1}{x^2+3}+\dfrac{1}{x^2+5}\right)=0\)
=>\(x^2-2=0\)
=>\(x^2=2\)
=>\(x=\pm\sqrt{2}\)

(1 + 22 + 333 + 4444) x (2 x 75 - 150)
= (1 + 22 + 333 + 4444) x (150 - 150)
= (1 + 22 + 333 + 4444) x 0
= 0
Chọn C
\(\left(1+22+333+4444\right)\times\left(75\times2-150\right)\)
\(=\left(1+22+333+4444\right)\times\left(150-150\right)\)
=0
=>Chọn C
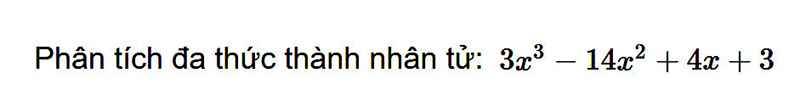



Gọi độ dài quãng đường từ thư viện đến trường là x(m)
(Điều kiện: x>0)
Thời gian Qiqi đi từ thư viện đến trường là \(\dfrac{x}{60}\left(phút\right)\)
Thời gian Weiling đi từ thư viện đến trường là \(\dfrac{x}{72}\left(phút\right)\)
Weiling đến trường trước Qiqi 4 phút và xuất phát sau 2 phút nên ta có: \(\dfrac{x}{60}-\dfrac{x}{72}=4+2=6\)
=>\(\dfrac{x}{360}=6\)
=>\(x=6\cdot360=2160\left(nhận\right)\)
Vậy: độ dài quãng đường từ thư viện đến trường là 2160(m)
Nếu đi từ thư viện đến trường, thời gian Weiling hoàn thành nhanh hơn Qiqi là:
4 + 2 = 6 (phút)
Tỉ lệ vận tốc Qiqi so với Weiling là: \(\dfrac{60}{72}=\dfrac{5}{6}\)
Cùng một quãng đường, vận tốc và thời gian là hai đại lượng tỉ lệ nghịch với nhau
Do đó tỉ lệ thời gian hoàn thành quãng đường Qiqi so với Weiling là: \(\dfrac{6}{5}\)
Coi thời gian Qiqi đi là 6 phần, Weiling đi là 5 phần
Hiệu số phần bằng nhau:
6 - 5 = 1 (phần)
Thời gian Qiqi đi là:
6 : 1 x 6 = 36 (phút)
Quãng đường từ thư viện đến trường là:
36 x 60 = 2160 (m)
Đáp số: 2160m