Lời giải:

a.

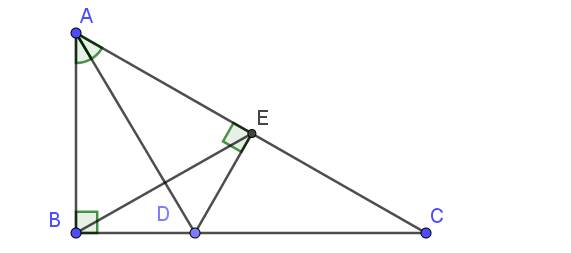
Tam giác $ABC$ vuông tại $B$ nên $\widehat{ABC}=90^0$

Xét tam giác $ABC$ có:

$\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0$ (tổng 3 góc trong 1 tam giác)

$\Rightarrow 90^0+30^0+\widehat{BAC}=180^0$

$\Rightarrow \widehat{BAC}=60^0$

b.

Xét tam giác $BAD$ và $EAD$ có:

$AD$ chung

$\widehat{BAD}=\widehat{EAD}$ (do $AD$ là phân giác $\widehat{A}$)

$\widehat{ABD}=\widehat{AED}=90^0$

$\Rightarrow \triangle BAD=\triangle EAD$ (ch-gn)

c.

Từ tam giác bằng nhau phần b suy ra $AB=AE$

$\Rightarrow ABE$ cân tại $A$

$\Rightarrow \widehat{ABE}=\widehat{AEB}$

Mà $\widehat{BAE}=60^0$ (kết quả phần a) nên:

$\widehat{ABE}=\widehat{AEB}=(180^0-\widehat{BAE}):2=(180^0-60^0):2=60^0$

Vậy $\widehat{ABE}=\widehat{AEB}=\widehat{BAE}=60^0$ nên $ABE$ là tam giác đều.

Hình vẽ:

Gọi A là biến cố "quả bóng lấy ra là số nguyên tố"

=>A={5}

=>n(A)=1

\(P\left(A\right)=\dfrac{1}{5}\)

 Gọi B là biến cố "Quả bóng lấy ra ghi số chia hết cho 5"

=>B={5;10;15;20;25}

=>n(B)=5

\(P\left(B\right)=\dfrac{5}{5}=1\)

 Gọi C là biến cố "Quả bóng lấy ra ghi số chia hết cho 6"

=>C=\(\varnothing\)

=>\(P\left(C\right)=0\)

a: Biến cố chắc chắn là biến cố B

b: \(P\left(A\right)=\dfrac{1}{5}\)

a, Biến cố "quả bóng lấy ra ghi số nguyên tố" là biến cố ngẫu nhiên

 Biến cố " quả bóng lấy ra ghi số chia hết cho 5" là biến cố chắc chắn 

Biến cố " quả bóng lấy ra ghi số chia hết cho 6" là biến cố không thể

b, Xác suất của biến cố"quả bóng lấy ra ghi số nguyên tố"là 1/5

Hình bạn tự vẽ nhé

a,Xét tam giác BAD và tam giác EDA:

AD chung

ABD=AED=90 độ( tam giác ABC vuông tại B, DE vuông góc AC)

BAD=CAD(AD là tia phân giác)

Suy ra tam giác BAD= tam giác EDA(cạnh huyền - góc nhọn)

b, Vì tam giác BAD= tam giác EDA (cmt)

Suy ra: AB=AE(2 cạnh tương ứng)

Suy ra A thuộc trung trực BE ₁

Vì tam giác BAD = tam giác EDA(CMA)

Suy ra:BD=DE

Suy ra: D thuộc trung trực BE ₂ 

Từ 1 và 2 

Suy ra AD là đường trung trực BE

c,AB=AE(cmt) ₃

BK=EC(gt) ₄

AB+BK=AK ₅

AE+EC=AC ₆

Từ 3,4,5,6

Suya ra AK =AC

Suy ra tam giác AKC cân tại A ₇

Mà AD là tia phân giác  ₈

_{Từ 7 và 8}

Suy ra AD là đg cao tam giác AKC

Xét tam giác AKC có:

Đg cao CB( tam giác ABC vuông tại B)

Đg cao AD (cmt)

Mà AD cắt CB tại D

Suy ra D là trực tâm tam giác AKC ₉

Suy ra KE là đg cao còn lại ₁₀ 

Từ 9,10

Suy ra D thuộc KE

Suy ra K,D,E thg hàng

a, P(x) = 6x^3 - 3x^2 + 5x - 1

    Q(x) = -6x^3 + 3x^2 - 2x + 7

b, P(x) + Q(x)

= ( 6x^3 - 3x^2 + 5x - 1 ) + ( -6x^3 +3x^2 - 2x +7 )

= 6x^3 - 3x^2 + 5x -1 + ( -6x^3 ) + 3x^2 - 2x +7

= [ 6x^3 + ( -6x^3) ] + (-3x^2 + 3x^2 ) + ( 5x - 2x ) + ( -1 +7 )

= 3x + 6

P(x) - Q(x)

= (6x^3 - 3x^2 + 5x - 1 ) - (-6x^3 + 3x^2 - 2x + 7 )

= 6x^3 - 3x^2 + 5x -1 - 6x^3 - 3x^2 + 2x - 7

= ( 6x^3 - 6x^3 ) + (-3x^2 - 3x^2 ) + ( 5x +2x ) + ( -1 - 7 )

= -6x^2 + 7x + ( -8)

Lời giải:
\(A=(\frac{-3}{4}x^2y^5).(4x^3y)=\frac{-3}{4}.4(x^2.x^3)(y^5.y)\\ =-3x^5y^6\)

Hệ số: $-3$

Phần biến: $x^5y^6$

Bậc: $5+6=11$

c.

Tại $x=-1$ và $y=1$ thì:

$A=-3(-1)^5.1^6=3$

a: Xét ΔBAE vuông tại A và ΔBDE vuông tại D có

BE chung

BA=BD

Do đó; ΔBAE=ΔBDE

=>EA=ED

=>ΔEAD cân tại E

Ta có: BA=BD

=>B nằm trên đường trung trực của AD(1)

Ta có: EA=ED

=>E nằm trên đường trung trực củaAD(2)

Từ (1),(2) suy ra BE là đường trung trực của AD

b: Xét ΔBAD có

AH,BE là các đường cao

AH cắt BE tại I

Do đó: I là trực tâm của ΔBAD

=>DI\(\perp\)AB

mà AC\(\perp\)AB

nên DI//AC
c: Gọi K là giao điểm của CF và BA

Xét ΔBKC có

BF,CA là các đường cao

BF cắt CA tại E

Do đó: E là trực tâm của ΔBKC

=>KE\(\perp\)BC

mà ED\(\perp\)BC

và KE,ED có điểm chung là E

nên K,E,D thẳng hàng

=>BA,ED,CF đồng quy

Bạn nên viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề và hỗ trợ tốt hơn nhé.