Đây là phương trình Pell loại 2 nhé bạn.

\(x^2-5y^2=-1\)    (1)

Xét phương trình liên kết với pt đã cho là \(x^2-5y^2=1\)     (2)

Ta thấy \(\left(9,4\right)\) là nghiệm nguyên dương nhỏ nhất của pt (2)

Xét hệ phương trình: \(\left\{{}\begin{matrix}9=x^2+5y^2\\4=2xy\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x^2+5y^2=9\\xy=2\end{matrix}\right.\)   (3). Hệ (3) có nghiệm nguyên dương duy nhất là \(\left(2,1\right)\)

Xét các dãy số nguyên dương \(\left\{x_n\right\},\left\{y_n\right\}\) xác định bởi:

\(\left\{{}\begin{matrix}x_0=2,x_1=38,x_{n+2}=18x_{n+1}-x_n\\y_0=1,y_1=17,y_{n+2}=18y_{n+1}-y_n\end{matrix}\right.\) với \(n\inℕ\)

Khi đó mọi cặp số \(\left(x_n,y_n\right)\) đều là nghiệm của pt đã cho.

VD: Chọn \(n=0\) thì \(\left(x_n,y_n\right)=\left(x_0;y_0\right)=\left(2,1\right)\). Thử lại: \(2^2-5.1^2=-1\) (thỏa mãn) 

 Chọn \(n=1\) thì \(\left(x_n;y_n\right)=\left(x_1;y_1\right)=\left(38;17\right)\). Thử lại:

\(38^2-5.17^2=-1\) (thỏa mãn)

 Dạng tổng quát của pt này là \(x^2-dy^2=-1\)     (1) với \(d\) là số nguyên dương không chính phương. 

 Khi đó xét pt liên kết với (1) là \(x^2-dy^2=1\)    (2). Gọi \(\left(a,b\right)\) là nghiệm nguyên dương nhỏ nhất của (2). 

 Xét hệ pt \(\left\{{}\begin{matrix}a=x^2+dy^2\\b=2xy\end{matrix}\right.\)  (3). Nếu hệ (3) có nghiệm nguyên dương thì (1) cũng có nghiệm nguyên dương. Gọi \(\left(u,v\right)\) là nghiệm nguyên dương duy nhất của (3) thì xét dãy số nguyên dương \(\left\{x_n\right\},\left\{y_n\right\}\) xác định bởi: 

 \(\left\{{}\begin{matrix}x_0=a,x_1=u^3+3duv^2,x_{n+2}=2ax_{n+1}-x_n\\y_0=b,y_1=dv^3+3u^2v,y_{n+2}=2ay_{n+1}-y_n\end{matrix}\right.\) với \(n\inℕ\)

Khi đó \(\left(x_n,y_n\right)\) là tất cả các nghiệm nguyên dương của pt đã cho.

ĐKXĐ: \(x\ne2\)

\(\dfrac{x^2}{2-x}+\dfrac{3x-1}{3}=\dfrac{5}{3}\)

\(\Leftrightarrow\dfrac{x^2}{2-x}=\dfrac{5}{3}-\dfrac{3x-1}{3}\)

\(\Leftrightarrow\dfrac{x^2}{2-x}=\dfrac{6-3x}{3}\)

\(\Leftrightarrow\dfrac{x^2}{2-x}=2-x\)

\(\Rightarrow x^2=\left(2-x\right)^2\)

\(\Leftrightarrow x^2=x^2-4x+4\)

\(\Leftrightarrow4x=4\)

\(\Leftrightarrow x=1\) (tm ĐKXĐ)

ĐKXĐ: \(x\ne0;x\ne2\)

\(\dfrac{x+2}{x}=\dfrac{x-3}{x-2}\)

\(\Rightarrow\left(x+2\right)\left(x-2\right)=x\left(x-3\right)\)

\(\Leftrightarrow x^2-4=x^2-3x\)

\(\Leftrightarrow-3x=-4\)

\(\Leftrightarrow x=\dfrac{4}{3}\) (tm ĐKXĐ)

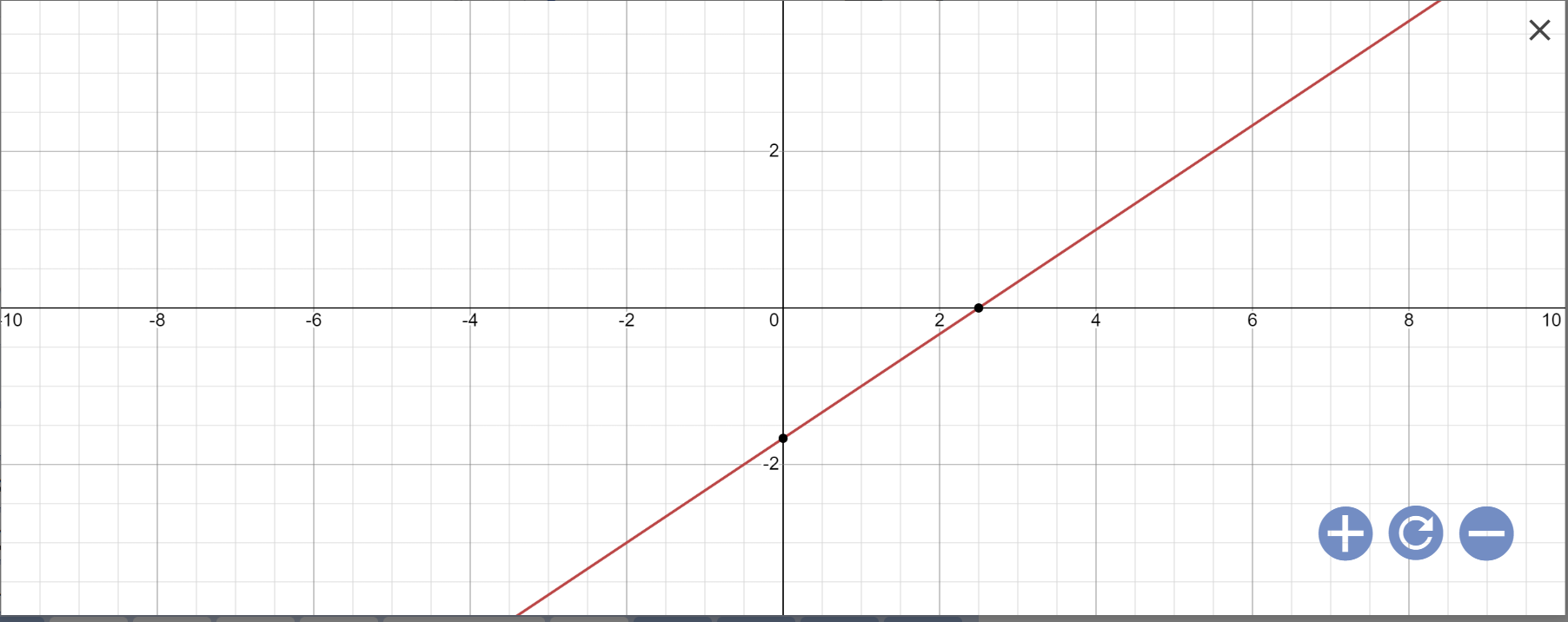
a: 2x-3y=5

=>2x=3y+5

=>\(x=\dfrac{3}{2}y+\dfrac{5}{2}\)

vậy: Nghiệm tổng quát là \(\left\{{}\begin{matrix}y\in R\\x=\dfrac{3}{2}y+\dfrac{5}{2}\end{matrix}\right.\)

Biểu diễn: 

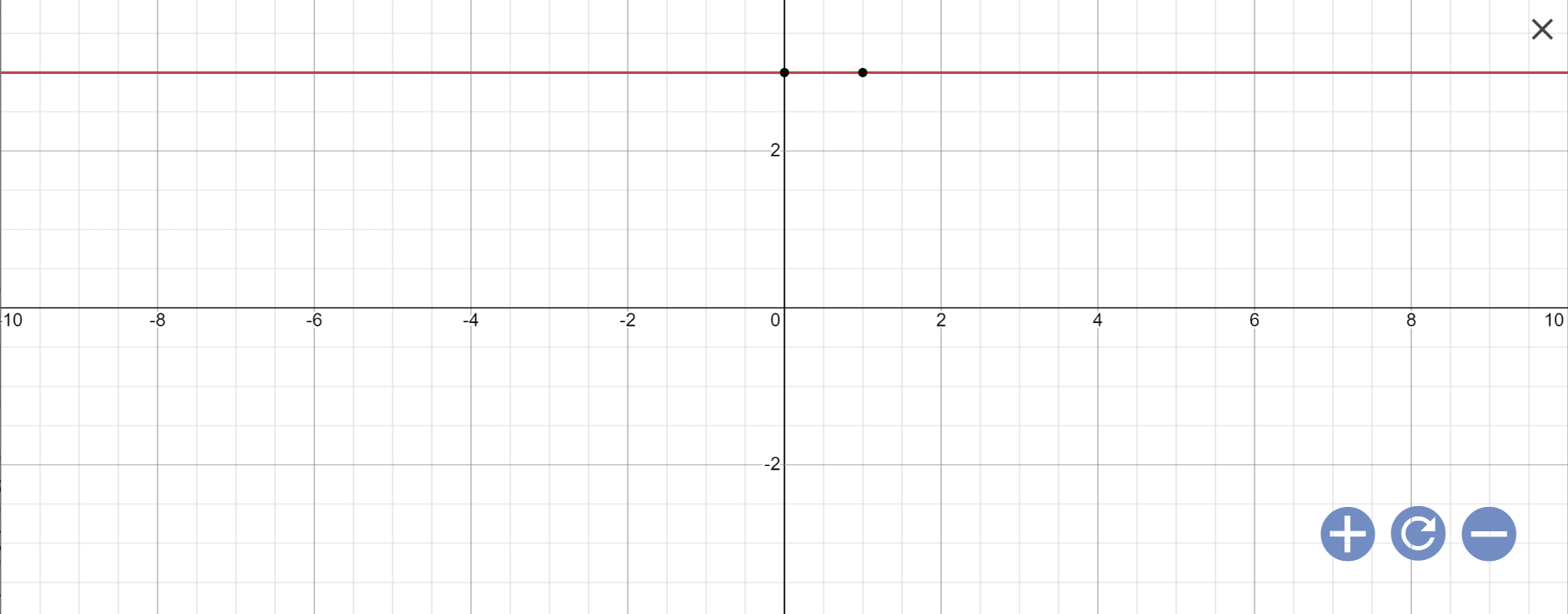
b: 0x+y=3

=>y=3

Vậy: Nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=3\end{matrix}\right.\)

Biểu diễn:

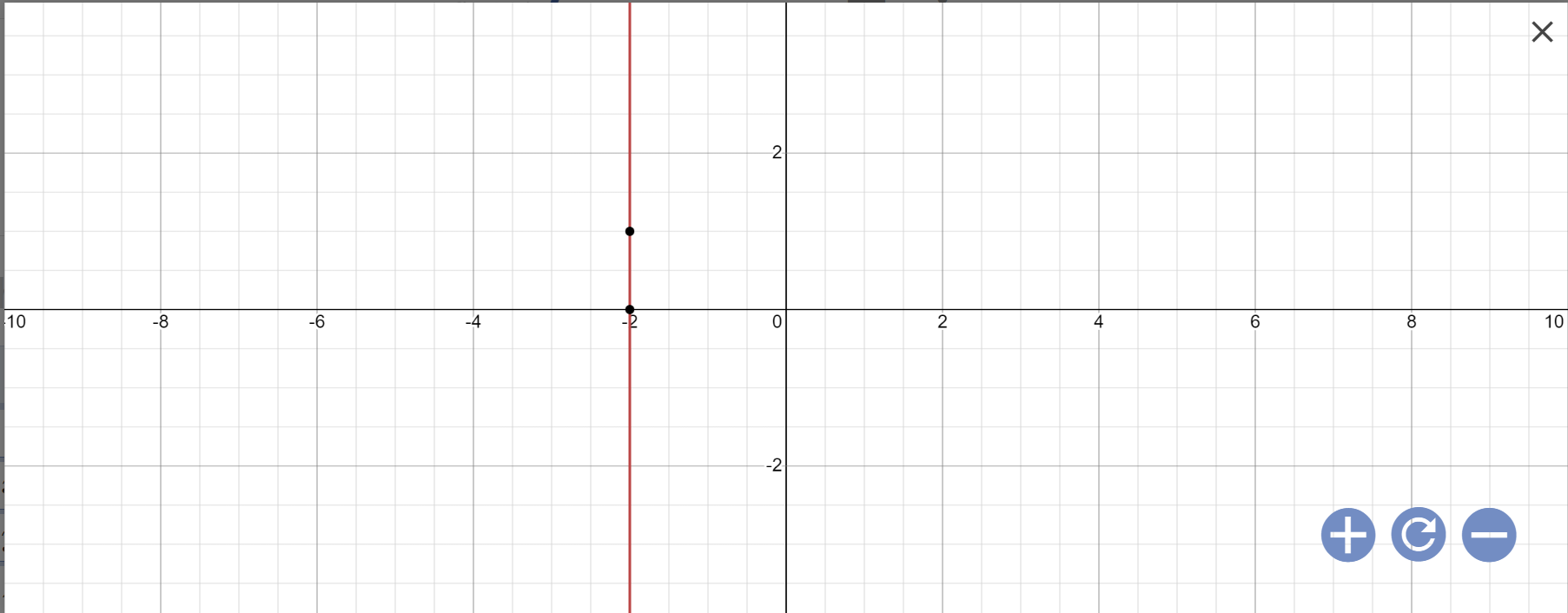
c: x+0y=-2

=>x=-2

Vậy: Nghiệm tổng quát là \(\left\{{}\begin{matrix}x=-2\\y\in R\end{matrix}\right.\)

Biểu diễn:

ĐKXĐ: \(x\ne-5\)

\(\dfrac{x+6}{x+5}+\dfrac{3}{2}=2\)

\(\Leftrightarrow\dfrac{x+6}{x+5}=\dfrac{1}{2}\)

\(\Rightarrow2\left(x+6\right)=1.\left(x+5\right)\)

\(\Leftrightarrow2x+12=x+5\)

\(\Leftrightarrow2x-x=5-12\)

\(\Leftrightarrow x=-7\) (tm ĐKXĐ)

ĐKXĐ: \(x\ne-5\)

\(\dfrac{x+6}{x+5}+\dfrac{3}{2}=2\)

=>\(\dfrac{x+6}{x+5}=2-\dfrac{3}{2}=\dfrac{1}{2}\)

=>\(2\left(x+6\right)=x+5\)

=>\(2x+12=x+5\)

=>2x-x=5-12

=>x=-7(nhận)

6:

Xét ΔMIN vuông tại I có \(tanN=\dfrac{MI}{NI}\)

=>\(NI=\dfrac{MI}{tanN}=\dfrac{11.5}{tan70}\simeq4,2\left(cm\right)\)

Xét ΔMIP vuông tại I có \(tanP=\dfrac{MI}{IP}\)

=>\(IP=\dfrac{MI}{tanP}=\dfrac{11.5}{tan38}\simeq14,7\left(cm\right)\)

NP=NI+IP=4,2+14,7=18,9(cm)

=>Chọn B

5: Xét ΔABC vuông tại A có 

\(sinC=\dfrac{AB}{BC}\)

=>\(BC=\dfrac{8}{sin30}=16\left(cm\right)\)

=>Chọn D

4:

\(\widehat{BAC}=27^0\)

Xét ΔBAC vuông tại B có \(tanBAC=\dfrac{BC}{BA}\)

=>\(BA=\dfrac{149}{tan27}\simeq292\left(m\right)\)

=>Chọn A

1: Xét ΔABC vuông tại A có \(tanC=\dfrac{AB}{AC}\)

=>\(\dfrac{AB}{10}=tan60\)

=>\(AB=10\cdot tan60=10\sqrt{3}\left(cm\right)\)

ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(BC=\sqrt{AB^2+AC^2}=20\left(cm\right)\)

=>Chọn C

2: ΔABC vuông tại A

=>\(BC^2=AB^2+AC^2\)

=>\(AB=\sqrt{8^2-6^2}=\sqrt{28}=2\sqrt{7}\left(cm\right)\)

Xét ΔABC vuông tại A có \(tanC=\dfrac{AB}{AC}=\dfrac{2\sqrt{7}}{6}=\dfrac{\sqrt{7}}{3}\cong0,88\)

=>Chọn C

3: \(B=tan20\cdot tan30\cdot tan40\cdot tan50\cdot tan60\cdot tan70\)

\(=\left(tan20\cdot tan70\right)\cdot\left(tan30\cdot tan60\right)\cdot\left(tan40\cdot tan50\right)\)

=1*1*1

=1

=>Chọn B

4:

\(\widehat{BAC}=27^0\)

Xét ΔBAC vuông tại B có \(tanBAC=\dfrac{BC}{BA}\)

=>\(BA=\dfrac{149}{tan27}\simeq292\left(m\right)\)

Vậy: Thuyền cách xa chân hải đăng 292m

Ta có:

\(4A+3B-\left(4A+2B\right)=x^2-2x+1-\left(x^2-2x+9\right)\)

\(\Rightarrow B=-8\)

Thay B vào \(4A+2B=x^2-2x+9\) được:

\(4A+2.\left(-8\right)=x^2-2x+9\)

\(\Rightarrow4A=x^2-2x+9+16\)

\(\Rightarrow4A=x^2-2x+25\)

\(\Rightarrow A=\dfrac{x^2-2x+25}{4}\)

Vậy...

\(\left\{{}\begin{matrix}4A+2B=x^2-2x+9\\4A+3B=x^2-2x+1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}B=-8\\4A+3B=x^2-2x+1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}B=-8\\4A+3.\left(-8\right)=x^2-2x+1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}B=-8\\4A-24=x^2-2x+1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}B=-8\\4A=x^2-2x+25\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}B=-8\\A=\dfrac{x^2-2x+25}{4}\end{matrix}\right.\)