cho tam giác abc cân tại a góc a=40 độ trên cạnh ab ac lần lượt lấy điểm d và e sao cho ad=ae chứng minh rằng da song song bc
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{\left(-3\right)^{10}\cdot15^5}{25^3\cdot\left(-9\right)^7}=\dfrac{3^{10}\cdot3^5\cdot5^5}{5^6\cdot\left(-1\right)\cdot3^{14}}=-\dfrac{3}{5}\)
\(\dfrac{\left(-3\right)^{10}.15^5}{25^3.\left(-9\right)^7}\)
\(=\dfrac{\left(-3\right)^{10}.\left(3.5\right)^5}{\left(5^2\right)^3.\left(-3^2\right)^7}\)
\(=\dfrac{\left(-3\right)^{10}.3^5.5^5}{5^6.\left(-3\right)^{14}}\)
\(=\dfrac{1.3^5.1}{5.3^4}\)
\(=\dfrac{3}{5.1}\)
\(=\dfrac{3}{5}\)

\(\dfrac{\left(\dfrac{2}{3}\right)^3\cdot\left(\dfrac{3}{4}\right)^2\cdot\left(-1\right)^5}{\left(\dfrac{2}{5}\right)\cdot\left(-\dfrac{5}{12}\right)^2}=\dfrac{\dfrac{2^3}{3^3}\cdot\dfrac{3^2}{4^2}\cdot\left(-1\right)}{\dfrac{2}{5}\cdot\dfrac{25}{144}}\)
\(=\dfrac{\dfrac{1}{2\cdot3}\cdot\left(-1\right)}{\dfrac{5}{72}}=-\dfrac{1}{6}\cdot\dfrac{72}{5}=-\dfrac{12}{5}\)

a: ta có: \(\widehat{MAB}=\widehat{ABC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AM//BC
ta có: \(\widehat{CAN}=\widehat{ACB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AN//BC
Ta có: AM//BC
NA//BC
mà AM,AN có điểm chung là A
nên M,A,N thẳng hàng
b: Vì M,A,N thẳng hàng nên \(\widehat{MAB}+\widehat{BAC}+\widehat{CAN}=180^0\)
=>\(\widehat{ABC}+\widehat{BAC}+\widehat{ACB}=180^0\)

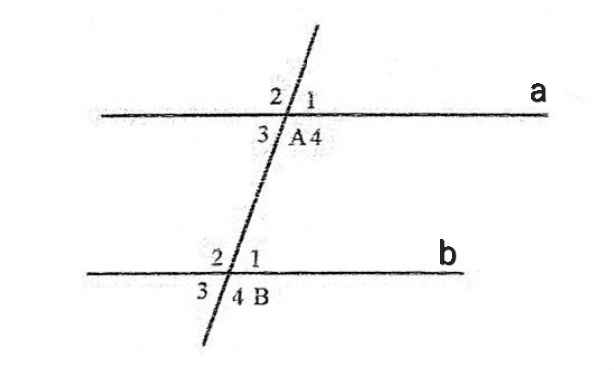
Ta có:
∠A₃ = ∠B₁ (gt)
Mà ∠A₃ và ∠B₁ là hai góc so le trong
⇒ a // b
⇒ ∠A₂ = ∠B₂ (đồng vị)
Do ∠A₃ + ∠A₄ = 180⁰ (kề bù)
Mà ∠A₃ = ∠B₁ (gt)
⇒ ∠B₁ + ∠A₄ = 180⁰


\(\dfrac{2}{1\cdot6}+\dfrac{2}{11\cdot16}+...+\dfrac{2}{x\left(x+5\right)}=\dfrac{41}{103}\\ =>\dfrac{2}{5}\left(\dfrac{5}{1\cdot6}+\dfrac{5}{6\cdot11}+...+\dfrac{5}{x\left(x+5\right)}\right)=\dfrac{41}{103}\\ =>1-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{11}+...+\dfrac{1}{x}-\dfrac{1}{x+5}=\dfrac{41}{103}:\dfrac{2}{5}=\dfrac{205}{206}\\ =>1-\dfrac{1}{x+5}=\dfrac{205}{206}\\ =>1-\dfrac{1}{x+5}=1-\dfrac{1}{206}\\ =>\dfrac{1}{x+5}=\dfrac{1}{206}\\ =>x+5=206\\ =>x=206-5=201\)


a: Ta có: xx'\(\perp\)AB
yy'\(\perp\)AB
Do đó: xx'//yy'
b: xx'//y'y
=>\(\widehat{ADC}=\widehat{C_1}\)(hai góc so le trong)
=>\(\widehat{C_1}=74^0\)
c: DE là phân giác của góc CDF
=>\(\widehat{FDE}=\dfrac{\widehat{FDC}}{2}=\dfrac{106^0}{2}=53^0\)
Xét ΔDEF có \(\widehat{x'FE}\) là góc ngoài tại F
nên \(\widehat{x'FE}=\widehat{FED}+\widehat{FDE}=70^0+53^0=123^0\)
 lời giải kèm hình vẽ
lời giải kèm hình vẽ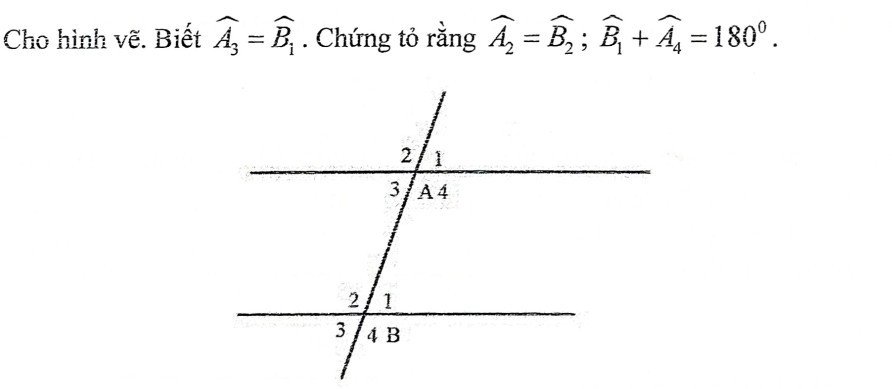 mng giúp e vs ạ
mng giúp e vs ạ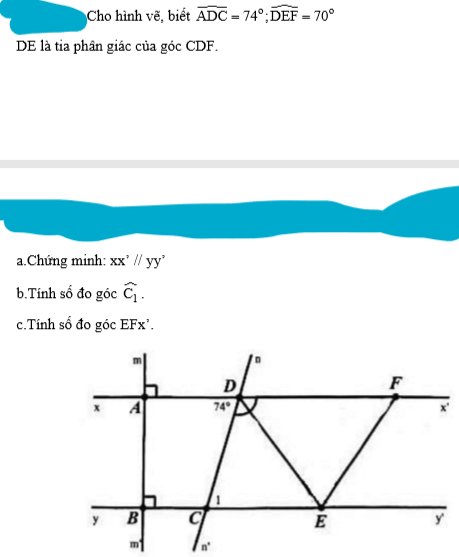
giúp tui pls
Sửa đề; DE//BC
Xét ΔABC có \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
nên DE//BC