một bếp ăn chuẩn bị cho 50 ngườiawn trong 60 ngày.Nhưng thực tế có 60 người ăn,hỏi số gạo đã chuẩn bị đủ dùng trong bao nhiêu ngày?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


9: \(A=\dfrac{\dfrac{1}{4}-5\cdot\left(\dfrac{3}{2}\right)^2}{10\dfrac{5}{9}+\left(-\dfrac{2}{3}\right)^2}=\dfrac{\dfrac{1}{4}-5\cdot\dfrac{9}{4}}{10+\dfrac{5}{9}+\dfrac{4}{9}}\)
\(=\dfrac{\dfrac{1}{4}-\dfrac{45}{4}}{10+1}=\dfrac{-44}{4}:11=-\dfrac{44}{44}=-1\)
\(B=\dfrac{5}{12}\cdot3,7-\dfrac{5}{12}\cdot6,7=\dfrac{5}{12}\cdot\left(3,7-6,7\right)\)
\(=\dfrac{5}{12}\cdot\left(-3\right)=-\dfrac{5}{4}\)
\(A-B=\left(-1\right)-\left(-\dfrac{5}{4}\right)=-1+\dfrac{5}{4}=\dfrac{1}{4}\)
10: \(P=\left(6,8;1,36-\dfrac{29}{3}:\dfrac{58}{9}\right):\dfrac{0.27^3}{0.09^3\cdot2}\)
\(=\left(5-\dfrac{29}{3}\cdot\dfrac{9}{58}\right):\dfrac{\left(0,3\right)^6\cdot3^3}{0,3^6\cdot2}\)
\(=\left(5-\dfrac{3}{2}\right):\dfrac{3^3}{2}=\dfrac{7}{2}\cdot\dfrac{2}{27}=\dfrac{7}{27}\)
\(P+\dfrac{1}{27}=\dfrac{7}{27}+\dfrac{1}{27}=\dfrac{8}{27}=\left(\dfrac{2}{3}\right)^3\)
=>\(P+\dfrac{1}{27}\) là bình phương của một số hữu tỉ

\(\dfrac{x}{\left(x+1\right)\left(x+4\right)}+\dfrac{x}{\left(x+4\right)\left(x+7\right)}+\dfrac{x}{\left(x+7\right)\left(x+10\right)}=\dfrac{x}{\left(x+1\right)\left(x+10\right)}\left(x\notin\left\{-1;-4;-7;-10\right\}\right)\\ \Leftrightarrow x\left[\dfrac{1}{\left(x+1\right)\left(x+4\right)}+\dfrac{1}{\left(x+4\right)\left(x+7\right)}+\dfrac{1}{\left(x+7\right)\left(x+10\right)}\right]=\dfrac{x}{\left(x+1\right)\left(x+10\right)}\\ \Leftrightarrow\dfrac{1}{3}x\left(\dfrac{1}{x+1}-\dfrac{1}{x+4}+\dfrac{1}{x+4}-\dfrac{1}{x+7}+\dfrac{1}{x+7}-\dfrac{1}{x+10}\right)=\dfrac{x}{\left(x+7\right)\left(x+10\right)}\\ \Leftrightarrow\dfrac{1}{3}x\left(\dfrac{1}{x+1}-\dfrac{1}{x+10}\right)=\dfrac{x}{\left(x+1\right)\left(x+10\right)}\\ \Leftrightarrow\dfrac{1}{3}x\cdot\dfrac{9}{\left(x+1\right)\left(x+10\right)}-\dfrac{x}{\left(x+1\right)\left(x+10\right)}=0\\ \Leftrightarrow\dfrac{3x}{\left(x+1\right)\left(x+10\right)}-\dfrac{x}{\left(x+1\right)\left(x+10\right)}\\ =0\\ \Leftrightarrow\dfrac{2x}{\left(x+1\right)\left(x+10\right)}=0\\ \Leftrightarrow2x=0\\ x=0\left(tm\right)\)


a) AB < AC (3 < 6)
=> B nằm giữa A và C
b) B nằm giữa A và C
=> AC = AB + BC
=> BC = AC - AB
=> BC = 6 - 3 = 3 (cm)
Mà: AB = 3 (cm) => AB = BC

Câu 4:
\(-0,40=\dfrac{-4}{10}=\dfrac{-2}{5}\)
\(0,25=\dfrac{25}{100}=\dfrac{1}{4}\)
\(-3,125=\dfrac{-3125}{1000}=\dfrac{-25}{8}\)
\(-5,24=\dfrac{-524}{100}=\dfrac{-131}{25}\)
Câu 1: -9,02<-1,23<0
0<0,5<2<13,1
Do đó: -9,02<-1,23<0,5<2<13,1
Câu 2:
\(-\dfrac{347}{10}=-34,7\)
\(\dfrac{6741}{100}=67,41\)
\(-\dfrac{53}{1000}=-0,053\)
\(\dfrac{86}{100}=0,86\)
Câu 3:
Số đối của 8,4 là -8,4
Số đối của -34,24 là 34,24
Số đối của -0,9 là 0,9
Số đối của 11,1 là -11,1

= 2x2 - 4xy - xy + 2y2
= 2x(x - 2y) - y(x - 2y)
= (2x - y)(x - 2y)

\(\widehat{aOt}=\dfrac{\widehat{aOc}}{2}\)(Ot là phân giác của góc aOc)
\(\widehat{bOz}=\dfrac{\widehat{dOb}}{2}\)(Oz là phân giác của góc dOb)
mà \(\widehat{aOc}=\widehat{bOd}\)(hai góc đối đỉnh)
nên \(\widehat{aOt}=\widehat{bOz}\)
mà \(\widehat{aOt}+\widehat{bOt}=180^0\)(hai góc kề bù)
nên \(\widehat{bOt}+\widehat{bOz}=180^0\)
=>Ot và Oz là hai tia đối nhau

Gọi đường thẳng (d): y=ax+b(a\(\ne\)0) là đường thẳng đi qua hai điểm (2;0); (-1;-2)
Thay x=2 và y=0 vào (d), ta được:
\(a\cdot2+b=0\)(1)
Thay x=-1 và y=-2 vào (d), ta được:
\(a\cdot\left(-1\right)+b=-2\left(2\right)\)
Từ (1),(2) ta có hệ phương trình: \(\left\{{}\begin{matrix}2a+b=0\\-a+b=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a+b+a-b=0-\left(-2\right)\\b=-2a\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3a=2\\b=-2a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{2}{3}\\b=-2\cdot\dfrac{2}{3}=-\dfrac{4}{3}\end{matrix}\right.\)
Vậy: (d): \(y=\dfrac{2}{3}x-\dfrac{4}{3}\)
=>\(\dfrac{2}{3}x-y=\dfrac{4}{3}\)
 các ban làm giùm mình câu 9,10
các ban làm giùm mình câu 9,10
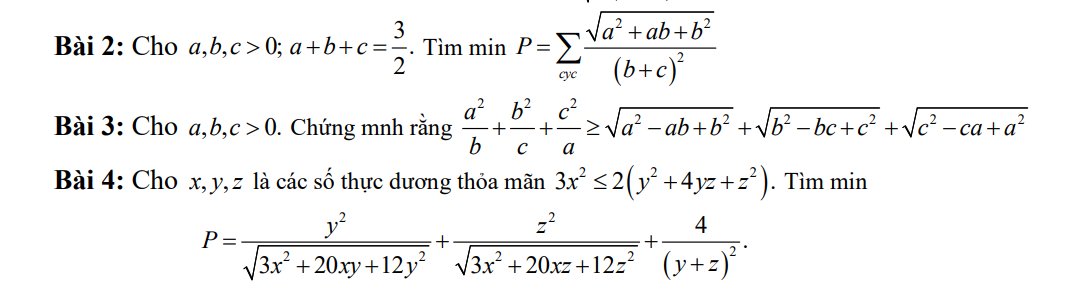
Đây là toán nâng cao chuyên đề hai đại lượng tỉ lệ nghịch, hôm nay Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Giải:
Một người ăn hết số gạo bếp ăn đã được chuẩn bị sẵn trong số ngày là:
60 x 50 = 3000 (ngày)
Thực tế có 60 người ăn số gạo đó nên số gạo đã chuẩn bị đủ ăn trong số ngày là:
3000 : 60 = 50 (ngày)
Đáp số: 50 ngày