So sánh $\dfrac{2022}{2021}$ và $\dfrac{2021}{2020}$.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a; \(\dfrac{-8}{10}\) = \(\dfrac{-8:2}{10:2}\) = \(\dfrac{-4}{5}\)
Vậy \(\dfrac{-4}{5}\) = \(\dfrac{-8}{10}\)
b; \(\dfrac{-120}{180}\) = \(\dfrac{-120:60}{180:60}\) = \(\dfrac{-2}{3}\)
Vậy \(\dfrac{-120}{180}=\dfrac{-2}{3}\)
a) Ta có: \(\dfrac{-8}{10}=\dfrac{-8:2}{10:2}=\dfrac{-4}{5}\)
Vậy hai phân số bằng nhau
b) Rút gọn
\(\dfrac{-120}{180}=\dfrac{-120:60}{180:60}=\dfrac{-2}{3}\)

a) Gọi A là biến cố "mặt xuất hiện là mặt 6 chấm"
\(\Rightarrow P\left(A\right)=\dfrac{17}{100}\)
b) Gọi B là biến cố "mặt xuất hiện là mặt có số chấm lẻ"
Số lần xuất hiện số chấm lẻ:
\(18+15+16=49\) (lần)
\(\Rightarrow P\left(B\right)=\dfrac{49}{100}\)
a) Xác xuất thực nghiệm xuất hiện mặt 6 chấm là: \(\dfrac{17}{100}\)
b) Số chấm lẻ là: 1, 3, 5
Số lần gieo được xúc xắc có số chấm lẻ là:
\(18+15+16=49\) (lần)
Xác xuất thực nghiệm xuất hiện được mặt có số chấm lẻ là: \(\dfrac{49}{100}\)

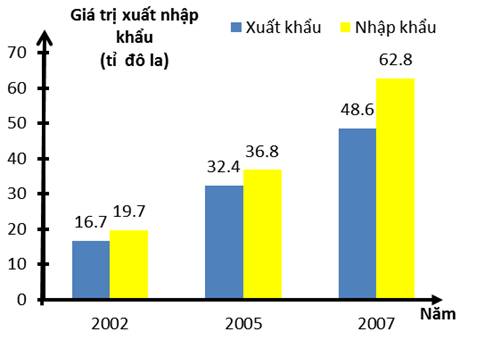
a) Năm 2002 giá trị xuất hàng hóa của Việt Nam là: \(16,7\) (tỉ đô la)
Năm 2002 giá trị nhập hàng hóa của Việt Nam là: \(19,7\) (tỉ đô la)
b) Tổng giá trị nhập khẩu của Việt Nam từ năm 2002 - 2007 là:
\(19,7+36,8+52,8=109,3\) (tỉ đô la)
a) Năm 2002, giá trị xuất khẩu hàng hóa của Việt Nam là: (tỉ đô la)
b) Tổng giá trị nhập khẩu hàng hóa của Việt Nam trong giai đoạn 2002 – 2007 là:
(tỉ đô la)

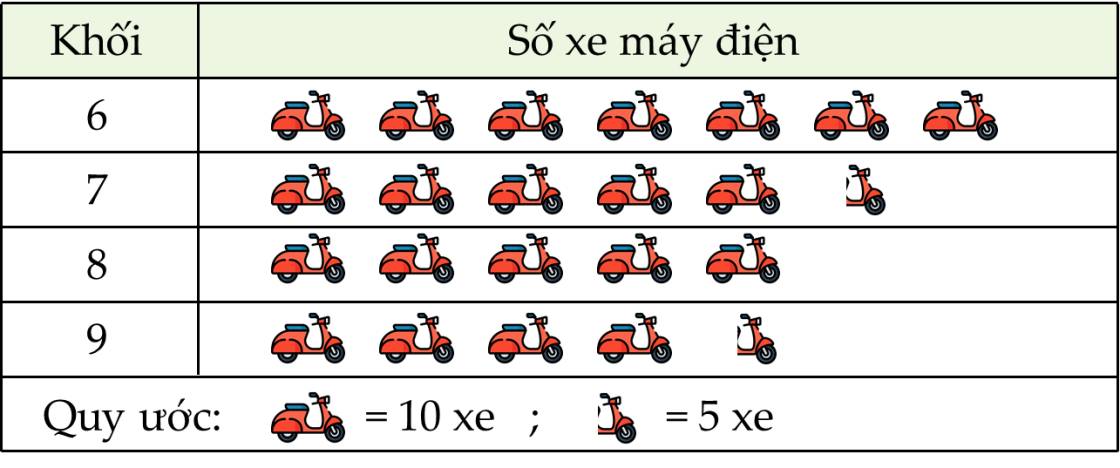
a)
| Khối | Số xe máy điện |
| 6 | \(7\cdot10=70\) |
| 7 | \(5\cdot10+5=55\) |
| 8 | \(5\cdot10=50\) |
| 9 | \(4\cdot10+5=45\) |
b) Khối ít xe nhất là khối 9
Tỉ số xe máy của khối đó vơi tổng số xe máy điện của toàn trường là:
\(45:\left(70+55+50+45\right)=\dfrac{9}{44}\)
a)
| Khối | Số xe máy điện |
| 6 | 70 |
| 7 | 55 |
| 8 | 50 |
| 9 | 45 |
b) Khối có ít xe nhất là khối 9.
+ Tổng số xe máy điện của toàn trường là (xe)
+ Tỉ số số xe máy điện của khối 9 với tổng số xe máy điện của toàn trường là:

Coi bể là 1 đơn vị.
1 giờ vòi thứ nhất chảy được:
1:6=\(\dfrac{1}{6}\) (bể)
1 giờ vòi thứ hai chảy được:
1:8=\(\dfrac{1}{8}\) (bể)
Nếu cùng chảy thì mỗi giờ cả hai vòi chảy được:
\(\dfrac{1}{6}+\dfrac{1}{8}=\dfrac{7}{24}\) (bể)
Đáp số: \(\dfrac{7}{24}\) bể
Một giờ vòi thứ nhất chảy được:
\(1:6=\dfrac{1}{6}\) (bể)
Một giờ vòi thứ hai chảy được:
\(1:8=\dfrac{1}{8}\) (bể)
Một giờ cả hai vòi chảy được:
\(\dfrac{1}{6}+\dfrac{1}{8}=\dfrac{7}{24}\) (bể)
ĐS: ...

B=\(\dfrac{1}{1.2.3.4}+\dfrac{1}{2.3.4.5}+\dfrac{1}{3.4.5.6}+...+\dfrac{1}{27.28.29.30}\)
B=\(\dfrac{1}{3}.\left(\dfrac{3}{1.2.3.4}+\dfrac{3}{2.3.4.5}+\dfrac{3}{3.4.5.6}+...+\dfrac{3}{27.28.29.30}\right)\)
B=\(\dfrac{1}{3}.\left(\dfrac{1}{1.2.3}-\dfrac{1}{2.3.4}+\dfrac{1}{2.3.4}-\dfrac{1}{3.4.5}+...+\dfrac{1}{27.28.29}-\dfrac{1}{28.29.30}\right)\)
B=\(\dfrac{1}{3}.\left(\dfrac{1}{1.2.3}-\dfrac{1}{28.29.30}\right)\)
B=\(\dfrac{1}{3}.\dfrac{1353}{8120}\)
B=\(\dfrac{451}{8120}\)

Bài 8:
a)\(2x-\dfrac{3}{5}=\dfrac{28}{15}\cdot\dfrac{6}{35}\)
\(\Rightarrow2x-\dfrac{3}{5}=\dfrac{8}{25}\)
\(\Rightarrow2x=\dfrac{8}{25}+\dfrac{3}{5}\)
\(\Rightarrow2x=\dfrac{23}{25}\)
\(\Rightarrow x=\dfrac{23}{25}:2=\dfrac{23}{50}\)
b) \(\dfrac{8}{23}\cdot\dfrac{46}{24}-x=\dfrac{1}{3}\)
\(\Rightarrow\dfrac{2}{3}-x=\dfrac{1}{3}\)
\(\Rightarrow x=\dfrac{2}{3}-\dfrac{1}{3}\)
\(\Rightarrow x=\dfrac{1}{3}\)
c) \(\dfrac{3}{22}-\dfrac{3}{4}x=\dfrac{27}{121}\cdot\dfrac{11}{9}\)
\(\Rightarrow\dfrac{3}{22}-\dfrac{3}{4}x=\dfrac{3}{11}\)
\(\Rightarrow\dfrac{3}{4}x=\dfrac{3}{22}-\dfrac{3}{11}\)
\(\Rightarrow\dfrac{3}{4}x=-\dfrac{3}{22}\)
\(\Rightarrow x=\dfrac{-3}{22}:\dfrac{3}{4}=-\dfrac{2}{11}\)
d) \(1-\dfrac{2}{3}x=\dfrac{49}{15}\cdot\dfrac{5}{7}\)
\(\Rightarrow1-\dfrac{2}{3}x=\dfrac{7}{3}\)
\(\Rightarrow\dfrac{2}{3}x=1-\dfrac{7}{3}\)
\(\Rightarrow\dfrac{2}{3}x=\dfrac{-4}{3}\)
\(\Rightarrow x=\dfrac{-4}{3}:\dfrac{2}{3}=-2\)

Vì abc là số có 3 chữ số và abc = (a+b+c)3
=> 99 < abc <1000
=> 13 < (a+b+c)3 < 103
=> 1 < (a+b+c) < 10
+) Nếu a+b+c = 9
Ta có: abc = (a+b+c)3 = 93 = 729
mà a+b+c = 7+2+9 = 18 9 (loại)
+) Nếu a+b+c = 8
Ta có abc = (a+b+c)3 = 83 = 512
mà a+b+c = 5+1+2 = 8 (đúng)
Vậy abc = 512
tick cho mik nhé, làm ơn
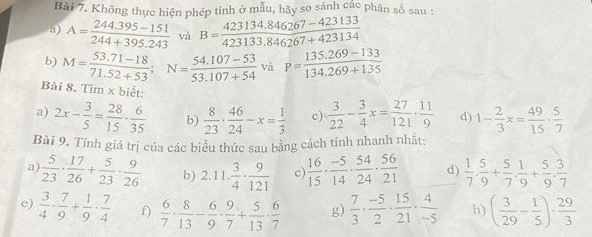
Ta có:
\(\dfrac{2022}{2021}=\dfrac{2021+1}{2021}=1+\dfrac{1}{2021}\)
\(\dfrac{2021}{2020}=\dfrac{2020+1}{2020}=1+\dfrac{1}{2020}\)
Mà: \(2021>2020\)
\(\Rightarrow\dfrac{1}{2021}< \dfrac{1}{2020}\)
\(\Rightarrow1+\dfrac{1}{2021}< 1+\dfrac{1}{2020}\)
\(\Rightarrow\dfrac{2022}{2021}< \dfrac{2021}{2020}\)
\(\dfrac{2022}{2021}=1+\dfrac{1}{2021}\)
\(\dfrac{2021}{2020}=1+\dfrac{1}{2020}\)
Do \(2021>2020\Rightarrow\dfrac{1}{2021}< \dfrac{1}{2020}\)
\(\Rightarrow1+\dfrac{1}{2021}< 1+\dfrac{1}{2020}\)
Vậy \(\dfrac{2022}{2021}< \dfrac{2021}{2020}\)