n+1/3n+4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(4+3^2+3^3+...+3^x=\left(3^{2024}-1\right):2\)
Đặt: \(S=4+3^2+3^3+...+3^x\)
\(\Rightarrow S=\dfrac{\left(3^{2024}-1\right)}{2}\Rightarrow2S=3^{2024}-1\)
\(S=4+3^2+3^3+...+3^x\)
\(S=1+3+3^2+3^3+...+3^x\)
\(3S=3\left(1+3+3^2+3^3+...+3^x\right)=3+3^2+3^3+3^4+...+3^{x+1}\)
\(3S-S=\left(3+3^2+3^3+3^4+...+3^{x+1}\right)-\left(1+3+3^2+3^3+...+3^x\right)\)
\(2S=3^{x+1}-1\)
\(\Rightarrow3^{x+1}-1=3^{2024}-1\)
\(3^{x+1}=3^{2024}\)
\(x+1=2024\)
\(x=2023\)
Vậy: \(x=2023\)

\(\dfrac{3}{17}\cdot\dfrac{6}{29}-\dfrac{35}{29}+2022\dfrac{3}{17}\)
\(=\dfrac{3}{17}\cdot\dfrac{6}{29}+2022+\dfrac{3}{17}-\dfrac{35}{29}\)
\(=\dfrac{3}{17}\left(\dfrac{6}{29}+1\right)-\dfrac{35}{29}+2022\)
\(=\dfrac{3}{17}\cdot\dfrac{35}{29}-\dfrac{35}{29}+2022\)
\(=\dfrac{35}{29}\left(\dfrac{3}{17}-1\right)+2022\)
\(=\dfrac{35}{29}\cdot\dfrac{-14}{17}+2022\)
\(=\dfrac{-490}{493}+2022=\dfrac{996356}{493}\)
chúng tôi muốn dựng hình hộp chữ nhật có kích thước 40 x 40 x 60 từ những hình lập phương giống nhau


\(\dfrac{17}{4}=\dfrac{16+1}{4}=4+\dfrac{1}{4}=4\dfrac{1}{4}\)

Số học sinh đạt danh hiệu xuất sắc là \(45\cdot\left(1-\dfrac{2}{3}\right)=45\cdot\dfrac{1}{3}=15\left(bạn\right)\)
Phân số chỉ số học sinh xuất sắc so với cả lớp là:
\(1-\dfrac{2}{3}=\dfrac{1}{3}\)
Số học sinh xuất sắc là:
\(45\times\dfrac{1}{3}=15\) (học sinh)

a: Xét ΔABH và ΔACH có
AB=AC
AH chung
HB=HC
Do đó: ΔAHB=ΔAHC
b: Ta có: HE//AB
=>\(\widehat{EHA}=\widehat{HAB}\)(hai góc so le trong)
mà \(\widehat{HAB}=\widehat{EAH}\)(ΔHAB=ΔHAC)
nên \(\widehat{EHA}=\widehat{EAH}\)
=>ΔEAH cân tại E

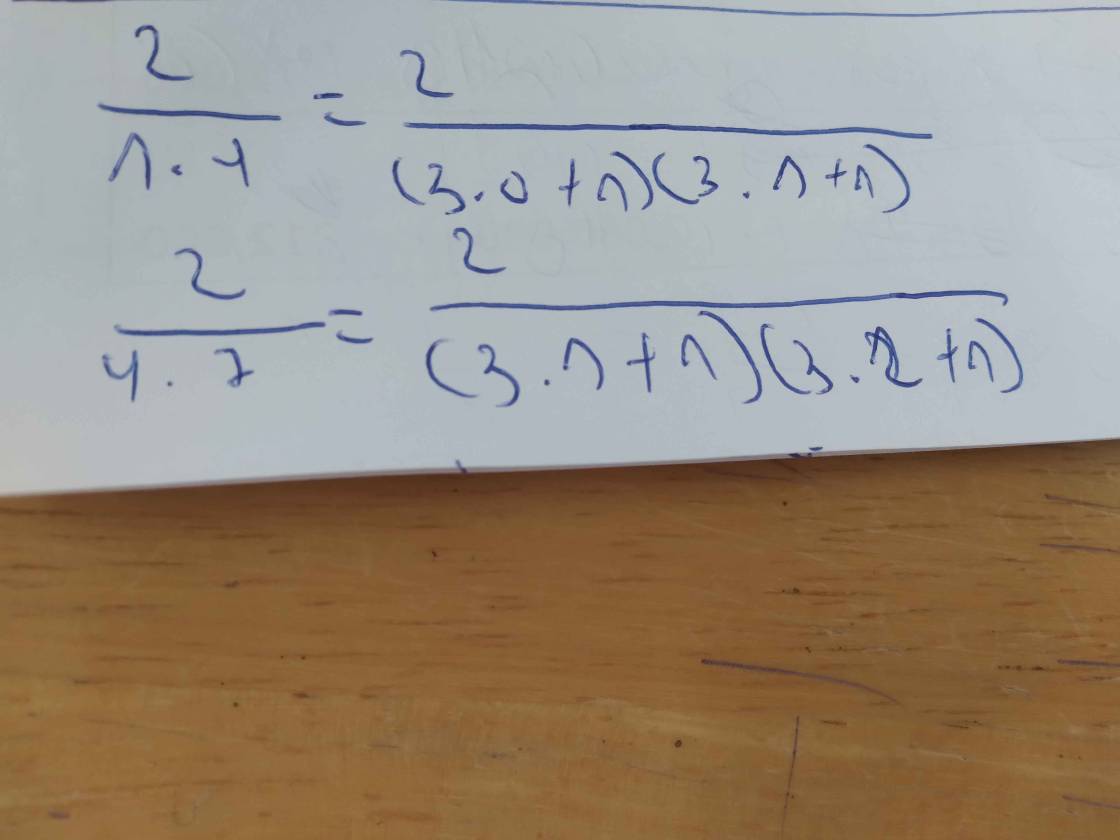

Đề yêu cầu gì bạn nhỉ?
A = \(\dfrac{n+1}{3n+4}\)
a; Điều kiện để A là phân số: 3n + 4 ≠ 0
n ≠ \(\dfrac{-4}{3}\)
Vậy để A là phân số thì n ≠ \(\dfrac{-4}{3}\)
b; Để A là số nguyên thì
n + 1 ⋮ 3n + 4
3.(n + 1) ⋮ 3n + 4
3n + 3 ⋮ 3n + 4
3n + 4 - 1 ⋮ 3n + 4
1 ⋮ 3n + 4
3n + 4 \(\in\) Ư(1) = {-1; 1}
Lập bảng ta có:
Theo bảng trên ta có: n = -1
Kết luận: Để phân số \(\dfrac{n+1}{3n+4}\) là số nguyên thì n = -1