Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a ) \(\dfrac{2017}{2018}=\) \(1-\dfrac{1}{2018}\) = > So sánh phần bù , phần thiếu
\(\dfrac{2019}{2020}\) = \(1-\dfrac{1}{2020}\)
Vì 1 \(-\dfrac{1}{2018}\) > \(1-\dfrac{1}{2020}\) nên
\(\dfrac{2017}{2018}>\dfrac{2019}{2020}\)
b)
Vì \(\dfrac{2018}{2017}>1\) và \(\dfrac{2020}{2019}>1\) nên
\(\dfrac{2018}{2017}=\dfrac{2019}{2020}\)
Chúng ta có 5 cách so sánh:
Cách 1 : So sánh mẫu của 2 phân số
Cách làm : Phân số nào có mẫu lớn hơn thì phân số đó bé hơn, có mẫu bé hơn thì lớn hơn
Cách 2 : So sánh tử của 2 phân số (ĐK:Mẫu của hai phân số phải cùng 1 mẫu)
Cách làm : Tử số của phân số nào lớn hơn thì p/số đó lớn hơn, tử của phân số nào bé hơn thì phân số đó bé hơn.
Cách 3 : So sánh số trung gian
Cách làm: Tìm 1 phân số hay 1 số nào đó gần liền kề phân số đó
Cách 4 : So sánh với 1
Cách 5 : So sánh phần bù , phần thiếu.

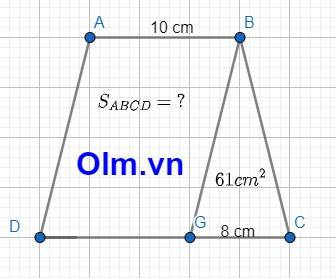
Đây là dạng toán nâng cao chuyên đề sự tăng giảm diện tích các hình, cấu trúc thi chuyên và thi học sinh giỏi các cấp. Hôm nay Olm.vn sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Giải
Theo bài ra ta có hình minh họa như sau:
Chiều cao của hình thang ban đầu là: 61 x 2 : 8 = 15,25 (cm)
đổi 1 dm = 10 cm
Chiều dài của hình thang ban đầu là: 10 + 8 = 18 (cm)
Diện tích hình thang ban đầu là: (18 + 10) x 15,25 : 2 = 213,5 (cm2)
Đáp số: 213,5 cm2

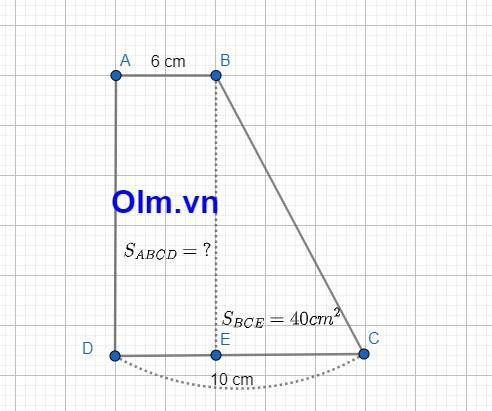
Đây là dang toán nâng cao chuyên đề sự tăng giảm diện tích các hính, cấu trúc thi chuyên, thi học sinh giỏi các cấp,thi violympic. Hôm nay Olm.vn sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Theo bài ra ta có hình minh họa sau:
Theo hình minh họa ta có:
Chiều cao của hình thang ban đầu là: 40x 2 : (10 - 6) = 20 (cm)
Diện tích hình thang ban đầu là: (6 + 10) x 20 : 2 = 160 (cm2)
Đáp số: 160 cm2

Olm chào em, đây là dạng toán nâng cao chuyên đề sự tăng giảm diện tích các hình. Cấu trúc thi chuyên, thi học sinh giỏi các cấp, thi violympic. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Giải:
Chiều cao của hình thang là: 60 x 2 : 10 = 12 (cm)
Diện tích ban đầu của hình thang là: 44 x 12 : 2 = 264 (cm2)
Đáp số: 264 cm2
Chiều cao của hình thang là: 60 . 2 : 10 = 12 (cm)
Diện tích ban đầu của hình thang là: 44 . 12 : 2 = 264 (cm2)

1 giờ 45 phút = 1,75 giờ
Quãng đường từ nhà đến thành phố:
24 × 1,75 = 42 (km)
Vận tốc xe máy:
24 × 5/3 = 40 (km/giờ)
Thời gian lúc về:
42 : 40 = 1,05 (giờ) = 1 giờ 3 phút

a: Thời gian cano đi từ A đến B là:
8h6p-7h30p=36p=0,6(giờ)
Vận tốc lúc xuôi dòng là 24:0,6=40(km/h)
Thời gian cano đi từ B về A là:
9h9p-8h6p-15p=1h3p-15p=48p=0,8(giờ)
Vận tốc lúc ngược dòng là:
24:0,8=30(km/h)
b: Vận tốc của bè gỗ là:
(40-30):2=5(km/h)
Thời gian bè gỗ trôi từ A đến B là:
24:5=4,8(giờ)

Thời gian ô tô đi hết quãng đường AB:
210 : 60 = 3,5 (giờ) = 3 giờ 30 phút
Ô tô đến B lúc:
6 giờ 45 phút + 3 giờ 30 phút + 15 phút = 10 giờ 30 phút

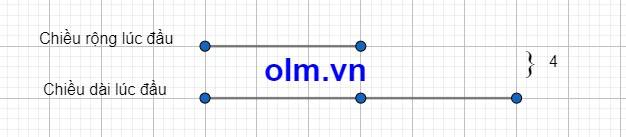
Đây là dạng toán nâng cao chuyên đề sự tăng giảm diện tích các hình, cấu trúc thi chuyên, thi học sinh giỏi, thi violympic. Hôm nay, Olm.vn sẽ hướng dẫn các em làm dạng này như sau:
Giải:
Theo có bài ra ta có hình minh họa như sau
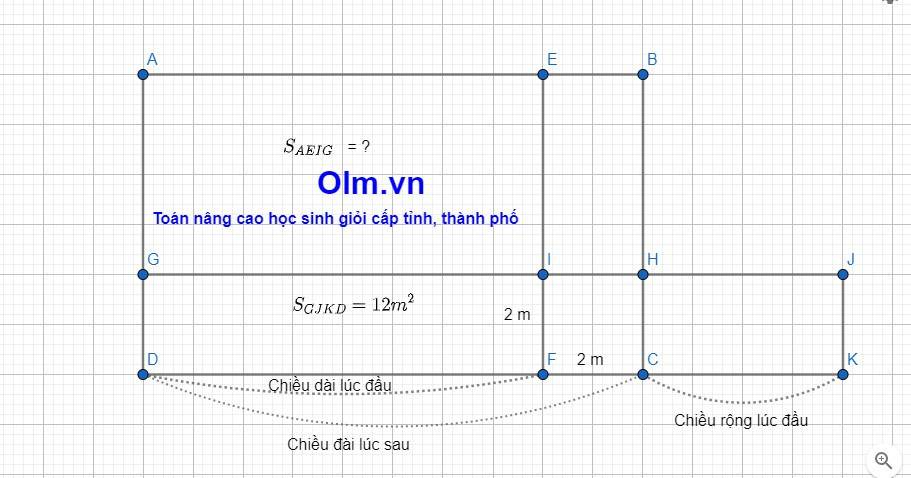
Tổng của chiều dài lúc sau và chiều rộng lúc đầu là:
12 : 2 = 6 (m)
Tổng của chiều dài lúc đầu và chiều rộng lúc đầu là:
6 - 2 = 4 (m)
Theo bài ra ta có sơ đồ:
Theo sơ đồ ta có:
Chiều dài ban đầu của hình chữ nhật là:
4 : (1 + 2) x 2 = \(\dfrac{8}{3}\) (m)
Chiều rộng lúc đầu là:
4 - \(\dfrac{8}{3}\) = \(\dfrac{4}{3}\) (m)
Diện tích ban đầu của mảnh vườn là:
\(\dfrac{8}{3}\times\dfrac{4}{3}=\dfrac{32}{9}\)(m2)
Đáp số: \(\dfrac{32}{9}\) (m2)
Ghi chú: Thử lại bài toán xem kết quả đúng sai ta có:
Diện tích lúc sau là: (\(\left(\dfrac{32}{3}+2\right)\times\left(\dfrac{4}{3}+2\right)\) = \(\dfrac{140}{9}\) (m2)
Diện tích của mảnh vườn hình chữ nhật tăng là:
\(\dfrac{140}{9}\) - \(\dfrac{32}{9}\) = 12 (m2)
Vậy đáp án của bài toán là đúng.






3 giờ 30 phút = 3,5 giờ
Vận tốc xe đạp:
63 : 3,5 = 18 (km/giờ)