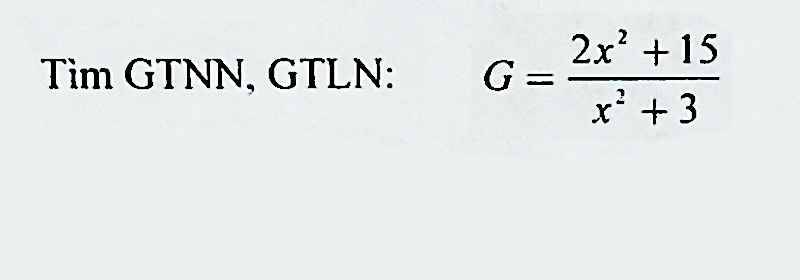
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{6}{5}\sqrt{1\dfrac{9}{16}}-\left(-\dfrac{3}{4}\right)^2:0,25\)
\(=\dfrac{6}{5}\cdot\sqrt{\dfrac{25}{16}}-\dfrac{9}{16}:0,25\)
\(=\dfrac{6}{5}\cdot\sqrt{\left(\dfrac{5}{4}\right)^2}-\dfrac{9}{16}:\dfrac{1}{4}\)
\(=\dfrac{6}{5}\cdot\dfrac{5}{4}-\dfrac{9\cdot4}{16}\)
\(=\dfrac{6}{4}-\dfrac{9}{4}\)
\(=\dfrac{6-9}{4}\)
\(=-\dfrac{3}{4}\)

Lời giải:
$A=\frac{1}{2}.\frac{2}{3}.\frac{3}{4}....\frac{1998}{1999}=\frac{1.2.3....1998}{2.3.4...1999}=\frac{1}{1999}$

`#3107.101107`
Đặt $A = 1 + 2 + 2^2 + 2^3 + ... + 2^{50}$
$2A = 2 + 2^2 + 2^3 + ... + 2^{51}$
$2A - A = (2 + 2^2 + 2^3 + ... + 2^{51}) - (1 + 2 + 2^2 + ... + 2^{50})$
$A = 2 + 2^2 + 2^3 + ... + 2^{51] - 1 - 2 - 2^2 - ... - 2^{50}$
$A = 2^{51} - 1$
Vậy, `A =` $2^{51} - 1.$

\(1\dfrac{2}{3}x+x=\left(-1,6\right)\\ \Rightarrow\dfrac{5}{3}x+x=\dfrac{18}{5}\\ \Rightarrow\dfrac{8}{3}x=\dfrac{18}{5}\\ \Rightarrow x=\dfrac{20}{27}\)
Sửa:
\(1\dfrac{2}{3}x+x=\left(-1,6\right)\\ \Rightarrow\dfrac{5}{3}x+x=-\dfrac{8}{5}\\ \Rightarrow\dfrac{8}{3}x=-\dfrac{8}{5}\\ \Rightarrow x=-\dfrac{20}{27}\)

Lời giải:
Nếu: $\frac{a}{b}< \frac{c}{d}$
$\Rightarrow \frac{a}{b}-\frac{c}{d}<0$
$\Rightarrow \frac{ad-bc}{bd}<0$
Do $bd>0$ nên $ad-bc<0$.
Khi đó:
$\frac{a}{b}-\frac{a+c}{b+d}=\frac{a(b+d)+b(a+c)}{b(b+d)}=\frac{ad-bc}{b(b+d)}<0$ do $ad-bc<0$ và $b(b+d)>0$
$\Rightarrow \frac{a}{b}< \frac{a+c}{b+d}$
Và:
$\frac{a+c}{b+d}-\frac{c}{d}=\frac{(a+c)d-c(b+d)}{d(b+d)}=\frac{ad-bc}{d(b+d)}<0$ do $ad-bc<0$ và $d(b+d)>0$)
$\Rightarrow \frac{a+c}{b+d}< \frac{c}{d}$
Vậy ta có đpcm.

a) Thể tích thùng xe tải:
5,6 . 2 . 2 = 22,4 (m³)
b) Thể tích gói hàng:
0,5³ = 0,125 (m³)
Số gói hàng tối đa thùng xe có thể chở:
22,4 : 0,125 = 179,2 (gói) ≈ 179 (gói)

\(-\dfrac{3}{7}.\dfrac{5}{7}+\left(-\dfrac{5}{7}\right).\dfrac{8}{11}+\dfrac{19}{7}\\ =\dfrac{5}{7}.\left(-\dfrac{3}{7}-\dfrac{8}{11}\right)+\dfrac{19}{7}\\ =\dfrac{5}{7}.-\dfrac{89}{77}+\dfrac{19}{7}\\ =\dfrac{445}{539}+\dfrac{19}{7}\\ =\dfrac{1908}{539}\)

Lời giải:
$G=\frac{2x^2+15}{x^2+3}=\frac{2(x^2+3)+9}{x^2+3}=2+\frac{9}{x^2+3}$
Vì $x^2\geq 0$ với mọi $x\in\mathbb{R}$
$\Rightarrow x^2+3\geq 3$
$\Rightarrow \frac{9}{x^2+3}\leq 3$
$\Rightarrow G=2+\frac{9}{x^2+3}\leq 2+3=5$.
Vậy $G_{\max}=5$. Giá trị này đạt được khi $x=0$
Biểu thức này không có giá trị min bạn nhé.