Cho (O; R), đường kính AB. tiếp tuyến tại M của đường tròn tâm o cắt 2 tiếp tuyến tại A và B lần lượt ở C và D. Vẽ (I, CD). Chứng minh AB tiếp xúc với (I) tại O.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Để phép chia trở thành phép chia hết, thương giữ nguyên thì số bị chia cần giảm là: 10 đơn vị
Một phép chia hết để thương giảm xuống hai đơn vị thì số bị chia cần giảm là:
124 x 2 = 248 (đơn vị)
Đấy số a chia cho 124 dư 10 trở thành phép chia hết và thương giảm đi 2 đơn vị thì số a cần giảm đi:
248 + 10 = 258 (đơn vị)
Đáp số: 258 đơn vị
Để giải bài toán này, ta cần tìm số a sao cho khi giảm đi một số đơn vị nào đó, thì khi chia cho 124, phép chia sẽ cho kết quả là một số nguyên và thương giảm đi 2 đơn vị.
Gọi số đơn vị cần giảm là x. Ta có phương trình:
(a - x) % 124 = 0 (phép chia cho 124 cho kết quả là số nguyên)
(a - x) // 124 - 2 = (a // 124) - 2 (thương giảm đi 2 đơn vị)
Từ phương trình trên, ta có hệ phương trình:
(a - x) % 124 = 0
(a - x) // 124 - (a // 124) = 2
Giải hệ phương trình trên, ta sẽ tìm được giá trị của x và a.

\(E=1.1+2.2+3.3+4.4+...+99.99\)
\(\Rightarrow E=1^2+2^2+3^2+4^2+...+99^2\)
\(\Rightarrow E=\dfrac{99.\left(99+1\right)\left(2.99+1\right)}{6}\)
\(\Rightarrow E=\dfrac{99.100.199}{6}\)
\(\Rightarrow E=33.50.199=328350\)
E = 1 x 1 + 2 x 2 + 3 x 3 + 4 x 4 +...+ 99 x 99
E = 1x(2-1) + 2 x (3-1)+...+ 99 x (100 -1)
D = 1 x 2 - 1 + 2 x 3 - 2 +...+ 99 x 100 - 99
D = 1x2 + 2 x 3 +...+ 99 x 100 - ( 1 + 2 +...+ 99)
Đặt A = 1x2 + 2 x 3 +...+ 99 x 100
B = 1 + 2 + ...+ 99
1x2 x 3 = 1x2x3
2x3x3 = 2x 3 x (4-1) = 2x3x4 - 1x2x3
3 x 4 x 3 = 3 x 4 x ( 5 - 2) = 3 x 4 x 5 - 2 x 3 x 4
................................................
99 x 100 x 3 = 99 x 100 x (101 - 98) = 99x100x101 - 98 x 99 x 100
Cộng vế với vế ta có: 3A = 99 x 100 x 101
A = 99 x 100 x 101 : 3 = 333300
B = 1 + 2 + 3 + ...+ 99
B = (99 + 1).[(99 -1):1 +1]:2 = 4950
E = 33300 - 4950 = 328350

\(\dfrac{1}{7}+\dfrac{1}{91}+\dfrac{1}{247}+\dfrac{1}{475}+\dfrac{1}{775}+\dfrac{1}{1147}\)
\(=\dfrac{1}{1.7}+\dfrac{1}{7.13}+\dfrac{1}{13.19}+\dfrac{1}{19.25}+\dfrac{1}{25.31}+\dfrac{1}{31.37}\)
\(=\dfrac{1}{6}\left(1-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{13}+\dfrac{1}{13}-\dfrac{1}{19}+\dfrac{1}{19}-\dfrac{1}{25}+\dfrac{1}{25}-\dfrac{1}{31}+\dfrac{1}{31}-\dfrac{1}{37}\right)\)
\(=\dfrac{1}{6}\left(1-\dfrac{1}{37}\right)\)
\(=\dfrac{1}{6}.\dfrac{36}{37}\)
\(=\dfrac{6}{37}\)
\(#Wendy.Dang\)


a) Do ABCD là hình bình hành
\(\Rightarrow AD=BC\) và \(AD\) // \(BC\)
Do \(AD\) // \(BC\) (cmt)
\(\Rightarrow\widehat{ADH}=\widehat{CBK}\) (so le trong)
Xét hai tam giác vuông: \(\Delta ADH\) và \(\Delta CBK\) có:
\(AD=BC\) (cmt)
\(\widehat{ADH}=\widehat{CBK}\) (cmt)
\(\Rightarrow\Delta ADH=\Delta CBK\) (cạnh huyền - góc nhọn)
\(\Rightarrow AH=CK\) (hai cạnh tương ứng)
Do \(AH\perp BD\) (gt)
\(CK\perp BD\) (gt)
\(\Rightarrow AH\) // \(CK\)
Xét tứ giác AHCK có:
\(AH\) // \(CK\) (cmt)
\(AH=CK\) (cmt)
\(\Rightarrow AHCK\) là hình bình hành
b) Do AHCK là hình bình hành (cmt)
\(I\) là trung điểm của HK (gt)
\(\Rightarrow I\) là trung điểm của AC
Do ABCD là hình bình hành (gt)
\(I\) là trung điểm của AC (cmt)
\(\Rightarrow I\) là trung điểm của BD
\(\Rightarrow IB=ID\)
a) Xét : \(\Delta ADHvà\Delta CBK\) có :
góc : AHD = góc : CKB ( = 90 độ )
AD=BC ( ABCD là hbh )
góc ADH = góc CBK ( 2 góc ở vị trí slt tạo bởi 2 đường thẳng song song là AD và BC )
Do đó : \(\Delta ADH\text{=}\Delta CBK\left(c.h-g.n\right)\)
\(\Rightarrow AH\text{=}CK\)
Xét t/g AHCK có : AH//CK ( cùng vuông góc với BD )
AH = CK (cmt)
Suy ra : t/g AHCK là hbh.
b) Từ a) : suy ra : AHCK là hbh.
Suy ra : AC cắt HK tại trung điểm của mỗi đường.
Mà I là trung điểm của HK.
Suy ra : I cũng là trung điểm của AC.
Ta có : ABCD là hbh.
Suy ra : AC cắt BD tại trung điểm của mỗi đường .
Mà I là trung điểm của AC.
Suy ra : I cũng là trung điểm của BD.
Suy ra : IB=ID.

a) Ta có : t/g ABCD là hbh
Suy ra : AD=BC
Mà E là trung điểm của AD ; F là trung điểm của BC
Suy ra : AE=DE=BF=CF
Xét tứ giác EBFD có : BF//ED ( BC//AD )
BF=ED ( cmt )
Suy ra : t/g EBFD là hbh.
b) Từ O là giao điểm của hai đường chéo của hbh ABCD hay là giao điểm của AC và BD.
Suy ra : O là trung điểm của BD hay 3 điểm B ; O ; D thẳng hàng
Ta có : t/g EBFD là hbh ( cmt )
Suy ra : BD cắt EF tại trung điểm của mỗi đường .
Mà O là trung điểm của BD
Suy ra : O cũng là trung điểm của EF.
suy ra : 3 điểm F;O;E thẳng hàng.
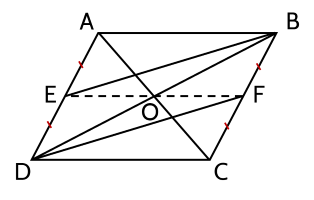
a) ABCD là hình bình hành nên AD = BC và AD // BC.
Mà E là trung điểm của AD nên AE = ED;
F là trung điểm của BC nên BF = FC.
Suy ra DE = BF.
Xét tứ giác EBFD có DE // BF (do AD // BC) và DE = BF nên là hình bình hành (dấu hiệu nhận biết).
b) Ta có O là giao điểm của hai đường chéo của hình bình hành ABCD nên O là trung điểm của BD.
Do EBFD là hình bình hành nên hai đường chéo BD và EF cắt nhau tại trung điểm của mỗi đường.
Mà O là trung điểm của BD nên O là trung điểm của EF.
Vậy ba điểm E, O, F thẳng hàng.

Bài 1 a, -5 \(\in\) Q; b, \(\dfrac{2}{-3}\) \(\notin\) I; c, \(\dfrac{3}{-5}\) \(\in\) R
d, N \(\subset\) Z \(\subset\) Q \(\subset\) R
e, -\(\sqrt{25}\) \(\notin\) N; f, \(\sqrt{17}\) \(\in\) R
Bài 2
a, -0,33 \(\in\) Q; b, 0,5241 \(\notin\) I;
c, 1,4142135... \(\in\) R; d, Q \(\subset\) R

ĐKXĐ: \(a\ne4\)
a) \(C=\left(\dfrac{2+\sqrt{a}}{2-\sqrt{a}}-\dfrac{2-\sqrt{a}}{2+\sqrt{a}}-\dfrac{4a}{a-4}\right):\left(\dfrac{2}{2-\sqrt{a}}-\dfrac{\sqrt{a}+3}{2\sqrt{a}-a}\right)\)
\(=\left[\dfrac{\left(2+\sqrt{a}\right)^2-\left(2-\sqrt{a}\right)^2}{\left(2+\sqrt{a}\right)\left(2-\sqrt{a}\right)}+\dfrac{4a}{4-a}\right]:\left[\dfrac{2\sqrt{a}-\sqrt{a}-3}{\sqrt{a}\left(2-\sqrt{a}\right)}\right]\)
\(=\dfrac{4+4\sqrt{a}+a-4+4\sqrt{a}-a+4a}{\left(2+\sqrt{a}\right)\left(2-\sqrt{a}\right)}.\dfrac{\sqrt{a}\left(2-\sqrt{a}\right)}{\sqrt{a}-3}\)
\(=\dfrac{4a+8\sqrt{a}}{\left(2+\sqrt{a}\right)\left(2-\sqrt{a}\right)}.\dfrac{\sqrt{a}\left(2-\sqrt{a}\right)}{\sqrt{a}-3}\)
\(=\dfrac{4\sqrt{a}\left(\sqrt{a}+2\right).\sqrt{a}\left(2-\sqrt{a}\right)}{\left(2+\sqrt{a}\right)\left(2-\sqrt{a}\right)\left(\sqrt{a}-3\right)}\)
\(=\dfrac{4a}{\sqrt{a}-3}\)


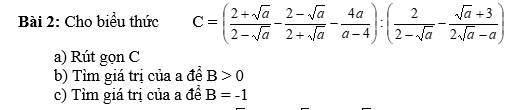
Dễ thấy ABDC là hình thang. Vì O, I lần lượt là trung điểm của AB, CD nên OI là đường trung bình của hình thang ABDC.
\(\Rightarrow\left\{{}\begin{matrix}OI//AC//BD\Rightarrow OI\perp AB\left(tạiO\right)\\OI=\dfrac{AC+BD}{2}=\dfrac{CM+DM}{2}=\dfrac{CD}{2}=R\end{matrix}\right.\) với R là bán kính của đường tròn \(\left(CD\right)\).
Từ đó suy ra AB tiếp xúc (I) tại O. (đpcm)