Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
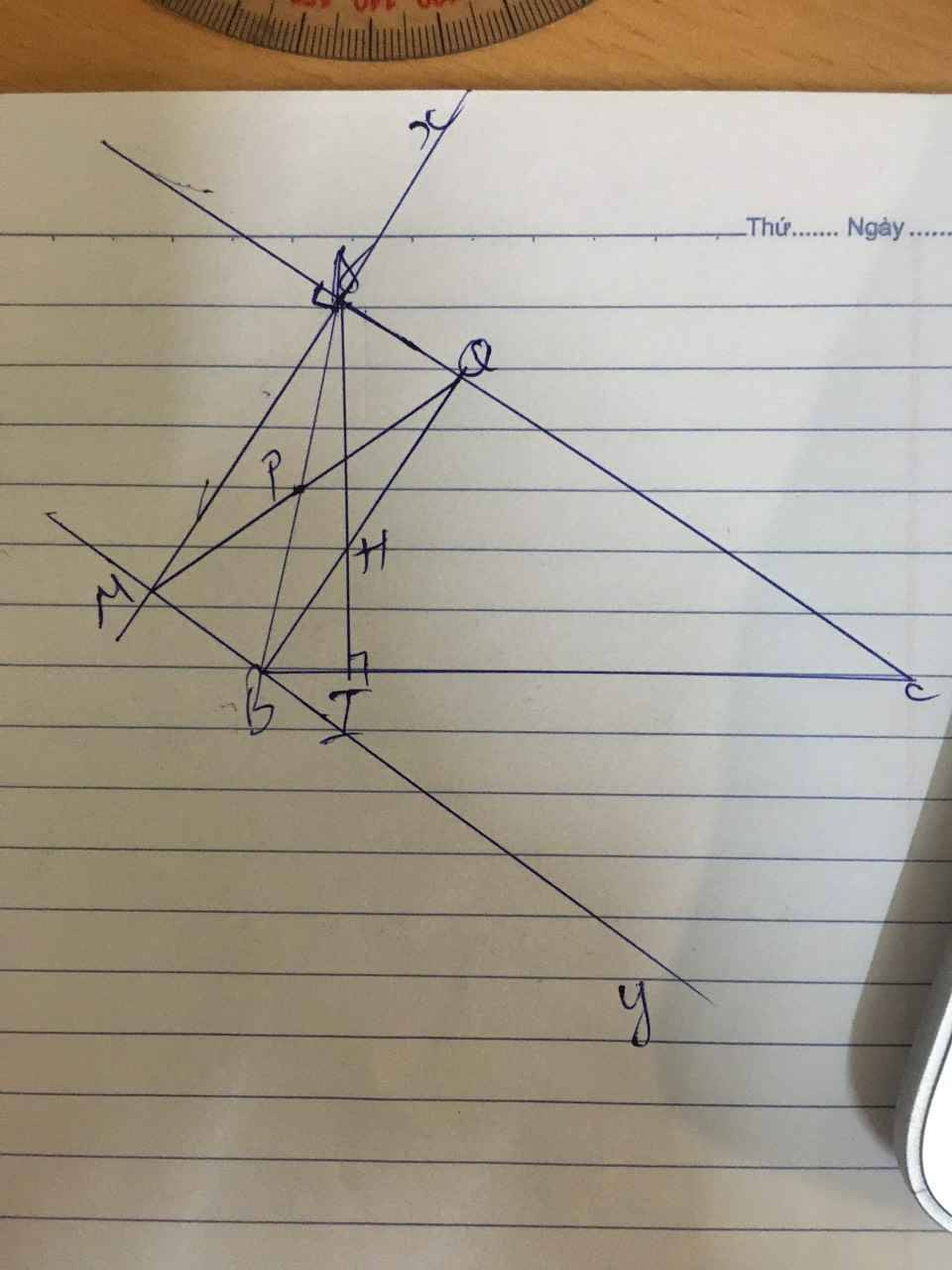
a) tứ giác AMPQ là hcn
b) ta có Ax \(\perp\) AC (gt)
M là giao điểm Ax và By ⇒ M ϵ Ax và M ϵ By
⇒ AM \(\perp\) AC
có BM // AC ⇒ AM\(\perp BM\)
xét △ APQ = △ BPM (gcg) ⇒ AQ = MB
xét tứ giác AQBM có AQ //MB; AQ = MB; AM\(\perp BM\)
⇒ AQBM là hcn
⇒ BQ \(\perp\)AC
xét △ ABC có AI, BQ là đường cao cắt nhau tại H ⇒ H là trực tâm của △ABC ⇒ CH \(\perp AB\)
c) xét △ vuông AIB có P là trung điểm AB ⇒ IP =AP = PB
mà AP = PB = PQ = MP( tc đường chéo của hcn)
⇒ IP = PQ ⇒ △ IPQ cân tại P
\(2x^2+x+1=2\left(x^2+\dfrac{1}{2}x+\dfrac{1}{16}\right)+\dfrac{7}{8}=2\left(x+\dfrac{1}{4}\right)^2+\dfrac{7}{8}\ge\dfrac{7}{8}>0;\forall x\)
= ( x2 + x + \(\dfrac{1}{4}\)) + x2 + \(\dfrac{3}{4}\)
= (x+1/2) 2 + x2 + 3/4
biểu thức trên luôn lớn hơn 0 với ∀x
\(a+b+c=0\Rightarrow a+b=-c\)
\(\Rightarrow\left(a+b\right)^3=\left(-c\right)^3\)
\(\Rightarrow a^3+b^3+3ab\left(a+b\right)=-c^3\)
\(\Rightarrow a^3+b^3+3ab\left(-c\right)=-c^3\) (do \(a+b+c=0\Rightarrow a+b=-c\))
\(\Rightarrow a^3+b^3+c^3=3abc\)
(a+b+c)3=a3+b3+c3+3(a+b)(b+c)(a+c) (1)
Ta có
a+b+c=0(2)
=>(a+b)=-c (3)
(b+c)=-a (4)
(a+c)=-b (5)
Thay (2) (3) (4) (5) vào (1)
0=a3+b3+c3=3(-c)(-a)(-b)
=> a3+b3+c3=3abc (đpcm)
\(P=\dfrac{a^3+b^3+3ab\left(a+b\right)-3ab\left(a+b\right)+c^3}{a^2+b^2+c^2-ab-bc-ca}=\dfrac{\left(a+b\right)^3+c^3-3ab\left(a+b+c\right)}{a^2+b^2+c^2-ab-bc-ca}\)
\(=\dfrac{\left(a+b+c\right)\left[\left(a+b\right)^2-\left(a+b\right)c+c^2\right]-3ab\left(a+b+c\right)}{a^2+b^2+c^2-ab-bc-ca}\)
\(=\dfrac{\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)}{a^2+b^2+c^2-ab-bc-ca}\)
\(=a+b+c=2022\)
\(3x^2-4xy+2y^2=3\)
\(\Leftrightarrow x^2+2\left(x-y\right)^2=3\)
\(\Rightarrow x^2\le3\Rightarrow\left[{}\begin{matrix}x^2=0\\x^2=1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\Rightarrow y^2=\dfrac{3}{2}\left(ktm\right)\\x=-1\Rightarrow2y^2+4y=0\Rightarrow y=\left\{-2;0\right\}\\x=1\Rightarrow2y^2-4y=0\Rightarrow y=\left\{0;2\right\}\end{matrix}\right.\)
\(\Rightarrow M=...\)
