x-4/8=5/18
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(1,\)
\(a,\dfrac{-9}{51}.\dfrac{17}{6}\)
\(=-1.\dfrac{1}{2}\)
\(=-\dfrac{1}{2}\)
\(b,\dfrac{-25}{32}.\left(-0,2\right)\)
\(=\dfrac{-25}{32}.-\dfrac{2}{10}\)
\(=\dfrac{-5}{16}.-\dfrac{1}{2}\)
\(=\dfrac{5}{32}\)
\(c,-15,2.3,5=-53,2\)
\(d,\dfrac{-8}{15}.1\dfrac{1}{4}\)
\(=\dfrac{-8}{15}.\dfrac{5}{4}\)
\(=\dfrac{-2}{3}.\dfrac{1}{1}\)
\(=\dfrac{-2}{3}\)
\(e,1\dfrac{2}{5}.\dfrac{-3}{14}\)
\(=\dfrac{7}{5}.\dfrac{-3}{14}\)
\(=\dfrac{1}{5}.\dfrac{-3}{2}\)
\(=-\dfrac{3}{10}\)
\(g,1\dfrac{1}{17}.1\dfrac{1}{36}\)
\(=\dfrac{18}{17}.\dfrac{37}{36}\)
\(=\dfrac{1}{17}.\dfrac{37}{2}\)
\(=\dfrac{37}{34}\)
\(#T.T\)



\(\left(1+\dfrac{1}{2}-\dfrac{1}{4}\right)^2\times\left(2+\dfrac{3}{7}\right)\\ =\left(\dfrac{4}{4}+\dfrac{2}{4}-\dfrac{1}{4}\right)^2\times\left(\dfrac{14}{7}+\dfrac{3}{7}\right)\\ =\left(\dfrac{5}{4}\right)^2\times\dfrac{17}{7}\\ =\dfrac{25}{16}\times\dfrac{17}{7}=\dfrac{425}{112}\)
Bạn nhấn vào biểu tượng Σ để nhập công thức toán học bạn nha!

\(#BecauseI'maStrongGirl\)

a) OA//IC => \(\widehat{CKB}=\widehat{AOK}=50^o\) (đồng vị)
OB//DE => \(\widehat{CID}=\widehat{CKB}=50^o\) (đồng vị)
b) Mà: \(\widehat{CIE}+\widehat{CID}=180^o\) (kề bù)
=> \(\widehat{CIE}=180^o-\widehat{CID}\)
=> \(\widehat{CIE}=180^o-50^o=130^o\)

Ta có: \(x^2+y^2+z^2+\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}=6 \)
\(\Leftrightarrow x^2+y^2+z^2+\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}-6=0\\ \Leftrightarrow\left(x^2+\dfrac{1}{x^2}-2\right)+\left(y^2+\dfrac{1}{y^2}-2\right)+\left(z^2+\dfrac{1}{z^2}-2\right)=0\\ \Leftrightarrow\left(x^2-2\cdot x^2\cdot\dfrac{1}{x^2}+\dfrac{1}{x^2}\right)+\left(y^2-2\cdot y^2\cdot\dfrac{1}{y^2}+\dfrac{1}{y^2}\right)+\left(z^2-2\cdot z^2\cdot\dfrac{1}{z^2}+\dfrac{1}{z^2}\right)=0\\ \Leftrightarrow\left(x-\dfrac{1}{x}\right)^2+\left(y-\dfrac{1}{y}\right)^2+\left(z-\dfrac{1}{z}\right)^2=0\)
Mà: \(\left\{{}\begin{matrix}\left(x-\dfrac{1}{x}\right)^2\ge0\forall x\\\left(y-\dfrac{1}{y}\right)^2\ge0\forall y\\\left(z-\dfrac{1}{z}\right)^2\ge0\forall z\end{matrix}\right.=>\left(x-\dfrac{1}{x}\right)^2+\left(y-\dfrac{1}{y}\right)^2+\left(z-\dfrac{1}{z}\right)^2\ge0\forall x,y,z\)
Dấu "=" xảy ra khi: \(\left\{{}\begin{matrix}x=\dfrac{1}{x}\\y=\dfrac{1}{y}\\z=\dfrac{1}{z}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2=1\\y^2=1\\z^2=1\end{matrix}\right.\)
\(P=x^{2024}+y^{2024}+z^{2024}\\=\left(x^2\right)^{1012}+\left(y^2\right)^{1012}+\left(z^2\right)^{1012}\\ =1^{1012}+1^{1012}+1^{1012}=3\)

Trên nửa mặt phẳng có bờ chứa tia Ox, có 2 tia oz và oy mà góc xOz < góc xOy ( 30độ < 110 độ) nên tia Oz nằm giữa 2 tia Ox và Oy
Ta có : xOz + zOy = xOy
30 + zOy = 110
zoy = 110 - 30 = 80
ot là tia phân giác của zOy nen zot = toy = 80 : 2 = 40
xot = zot + xoz = 40 + 30 = 70
vậy
yOz = 80 độ
zOt = 40 độ
xOt = 70 độ

\(\left\{{}\begin{matrix}x-ay=a\\ax+y=1\end{matrix}\right.\)
Để hpt có nghiệm thì: \(\dfrac{1}{a}\ne\dfrac{-a}{1}\Leftrightarrow a^2\ne-1\) (luôn đúng)
\(\Leftrightarrow\left\{{}\begin{matrix}x-ay=a\\a^2x+ay=a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(a^2+1\right)x=2a\\ax+y=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2a}{a^2+1}\\\dfrac{2a^2}{a^2+1}+y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2a}{a^2+1}\\y=1-\dfrac{2a^2}{a^2+1}=\dfrac{1-a^2}{a^2+1}\end{matrix}\right.\)
Ta có: \(\left\{{}\begin{matrix}\text{x}>0\\y>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2a}{a^2+1}>0\\\dfrac{1-a^2}{a^2+1}>0\end{matrix}\right.\)
Mà: \(a^2+1>0\forall a=>\left\{{}\begin{matrix}2a>0\\1-a^2>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a>0\\-1< a< 1\end{matrix}\right.\Leftrightarrow0< a< 1\)

a: \(8^{24}=\left(2^3\right)^{24}=2^{72};16^{20}=\left(2^4\right)^{20}=2^{80}\)
mà 72<80
nên \(8^{24}< 16^{20}\)
b: \(\left(-\dfrac{1}{25}\right)^{37}=-\left(\dfrac{1}{5}\right)^{74}=-\dfrac{1}{5^{74}};\left(-\dfrac{1}{125}\right)^{23}=-\dfrac{1}{\left(5^3\right)^{23}}=-\dfrac{1}{5^{69}}\)
\(5^{74}>5^{69}\)
=>\(\dfrac{1}{5^{74}}< \dfrac{1}{5^{69}}\)
=>\(-\dfrac{1}{5^{74}}>-\dfrac{1}{5^{69}}\)
=>\(\left(-\dfrac{1}{25}\right)^{37}>\left(-\dfrac{1}{125}\right)^{23}\)
c: \(A=\dfrac{3}{7^3}+\dfrac{5}{7^4}=\dfrac{3\cdot7+5}{7^4}=\dfrac{26}{7^4}\)
\(B=\dfrac{5}{7^3}+\dfrac{3}{7^4}=\dfrac{5\cdot7+3}{7^4}=\dfrac{38}{7^4}\)
mà 26<38
nên A<B
d: \(10A=\dfrac{10^8+10}{10^8+1}=1+\dfrac{9}{10^8+1}\)
\(10B=\dfrac{10^9+10}{10^9+1}=1+\dfrac{9}{10^9+1}\)
Ta có: \(10^8+1< 10^9+1\)
=>\(\dfrac{9}{10^8+1}>\dfrac{9}{10^9+1}\)
=>\(\dfrac{9}{10^8+1}+1>\dfrac{9}{10^9+1}+1\)
=>10A>10B
=>A>B





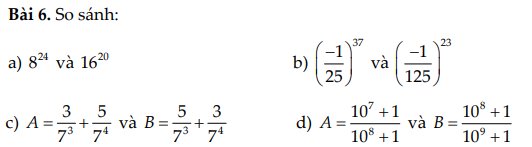
\(x-\dfrac{4}{8}=\dfrac{5}{18}\\ x=\dfrac{5}{18}+\dfrac{4}{8}\\ x=\dfrac{5}{18}+\dfrac{1}{2}\\ x=\dfrac{5}{18}+\dfrac{9}{18}\\ x=\dfrac{5+9}{18}\\ x=\dfrac{14}{18}\\ x=\dfrac{7}{9}\)