Xét tg ABC có

\(\widehat{C}+\widehat{ABC}+\widehat{BAC}=180^o\) (tổng các góc trong 1 tg bằng 360 độ)

Ta có Ax//By

\(\Rightarrow\widehat{ABy}+\widehat{BAx}=180^o\) (2 góc trong cùng phía)

\(\Rightarrow\widehat{C}+\widehat{ABC}+\widehat{ABy}+\widehat{BAC}+\widehat{BAx}=180^o+180^o=360^o\)

\(\Rightarrow\widehat{C}+\widehat{B}+\widehat{A}=360^o\)

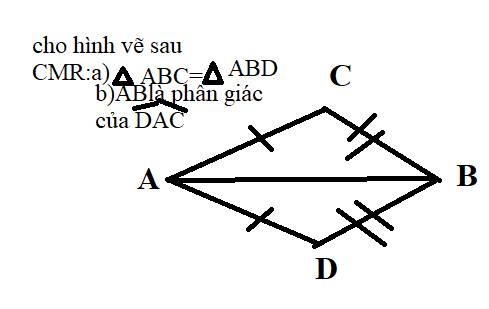
a) Xét ∆ABC và ∆ABD có:

AB là cạnh chung

AC = AD (gt)

BC = BD (gt)

⇒ ∆ABC = ∆ABD (c-c-c)

b) Do ∆ABC = ∆ABD (cmt)

⇒ ∠BAC = ∠BAD (hai góc tương ứng)

⇒ AB là tia phân giác của ∠DAC

\(2^{x+2}\cdot3^{x+1}\cdot5^x=10800\\\Rightarrow2^x\cdot2^2\cdot3^x\cdot3\cdot5^x=10800\\\Rightarrow(2^x\cdot3^x\cdot5^x)\cdot(2^2\cdot3)=10800\\\Rightarrow(2\cdot3\cdot5)^x\cdot(4\cdot3)=10800\\\Rightarrow30^x\cdot12=10800\\\Rightarrow30^x=10800:12\\\Rightarrow30^x=900\\\Rightarrow30^x=30^2\\\Rightarrow x=2\)

\(2^{x+2}.3^{x+1}.5^x=10800\\ \Leftrightarrow2^x.2^2.3^x.3.5^x=10800\\ \Leftrightarrow12.\left(2.3.5\right)^x=10800\\ \Leftrightarrow12.30^x=10800\\ \Leftrightarrow30^x=\dfrac{10800}{12}=900=30^2\\ Vậy:x=2\)

          \(\dfrac{a}{b}\) = \(\dfrac{c}{d}\)

          \(\dfrac{a}{c}\) = \(\dfrac{b}{d}\)

   \(\dfrac{a}{c}\)  =  \(\dfrac{5a}{5c}\) = \(\dfrac{3b}{3d}\) Áp dụng tính chất dãy tỉ số bằng nhau ta có:

      \(\dfrac{a}{c}\) =   \(\dfrac{5a+3b}{5c+3d}\) (1) 

       \(\dfrac{a}{c}\) = \(\dfrac{5a-3b}{5c-3d}\)  (2)

Kết hợp (1) và (2) ta có:

       \(\dfrac{5a+3b}{5c+3d}\) =  \(\dfrac{5a-3b}{5c-3d}\) 

⇒   \(\dfrac{5a+3b}{5a-3b}\) =  \(\dfrac{5c+3d}{5c-3d}\) (đpcm)

b;   \(\dfrac{a}{b}\) = \(\dfrac{c}{d}\) 

      \(\dfrac{a}{b}\) =  \(\dfrac{3a}{3b}\) = \(\dfrac{2c}{2d}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

     \(\dfrac{a}{b}\) = \(\dfrac{3a+2c}{3b+2d}\) (đpcm)

a) 3x = 7y ⇒ x/7 = y/3

⇒ x/7 = 2y/6

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

x/7 = 2y/6 = (x - 2y)/(7 - 6) = 2/1 = 2

x/7 = 2 ⇒ x = 2.7 = 14

y/3 = 2 ⇒ y = 2.3 = 6

Vậy x = 14; y = 6

b) x/2 = y/3 ⇒ x/6 = y/9 (1)

x/3 = z/4 ⇒ x/6 = z/8 (2)

Từ (1) và (2) ⇒ x/6 = y/9 = z/8

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

x/6 = y/9 = z/8 = (x + y - z)/(6 + 9 - 8) = 7/7 = 1

x/6 = 1 ⇒ x = 1.6 = 6

y/9 = 1 ⇒ y = 1.9 = 9

z/8 = 1 ⇒ z = 1.8 = 8

Vậy x = 6; y = 9; z = 8

c) x/2 = y/3 ⇒ x/10 = y/15 ⇒ 2x/20 = y/15 (3)

y/5 = z/4 ⇒ y/15 = z/12 (4)

Từ (3) và (4) ⇒ 2x/20 = y/15 = z/12

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

2x/20 = y/15 = z/12 = (2x - y + z)/(20 - 15 + 12) = 17/17 = 1

2x/20 = 1 ⇒ x = 1.20 : 2 = 10

y/15 = 1 ⇒ y = 1.15 = 15

z/12 = 1 ⇒ z = 1.12 = 12

Vậy x = 10; y = 15; z = 12

\(A=\dfrac{6+3^2.3-6+3^2}{3^2+3.3^2-3^4}=\dfrac{\left(6-6\right)+3^2\left(3+1\right)}{3^2\left(1+3-3^2\right)}\\ =\dfrac{0+3^2.4}{3^2.\left(-5\right)}=\dfrac{-4}{5}\)