Bài 3. Gọi số bông hoa điểm tốt của ba Hiệp, Bắc, Việt lần lượt là: 

\(x;y;z\)  (quyển sách);\(x;y;z\)\(\in\)N

Theo bài ra ta có: \(\dfrac{x}{3}\) = \(\dfrac{y}{2}\) = \(\dfrac{z}{4}\)

         Áp dụng tính chất dãy tỉ số bằng nhau ta có:

               \(\dfrac{x}{3}\) = \(\dfrac{y}{2}\) = \(\dfrac{z}{4}\) = \(\dfrac{x+y+z}{3+2+4}\)  =  \(\dfrac{72}{9}\) = 8

Số bông hoa điểm tốt của Hiệp là: 8 x 3 = 24 (bông)

Số bông hoa điểm tốt của Bắc là:  8 x 2 = 16 (bông)

Số bông hoa điểm tốt của Việt là:   8 x 4 = 32 (bông)

Kết luận:... 

                              Bài 4: 

    Gọi số học sinh của lớp 7A; 7B; 7C lần lượt là: 

               \(x;y;z\) (học sinh) \(x;y;z\in N\)

    Theo bài ra ta có:

                 \(\dfrac{x}{2}=\dfrac{y}{4}=\dfrac{z}{6}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

                 \(\dfrac{x}{2}=\dfrac{y}{4}=\dfrac{z}{6}\) = \(\dfrac{z-y}{6-4}\) = \(\dfrac{6}{2}\) = 3

Số học sinh giỏi lớp 7A là: 3 x 2 = 6 (học sinh)

Số học sinh giỏi lớp 7B là 3 x 4 = 12 (học sinh)

Số học sinh giỏi lớp 7C là: 3 x 6 = 18 (học sinh)

KL...

7^x.1+7^x.7²=2450

7^x(1+49)=2450

7^x.50=2450

7^x=2450:50

7^x=49=7²

=>x=2.

Đây nhé

cảm ơn

Đề lỗi hiển thị. Bạn xem lại nhé.

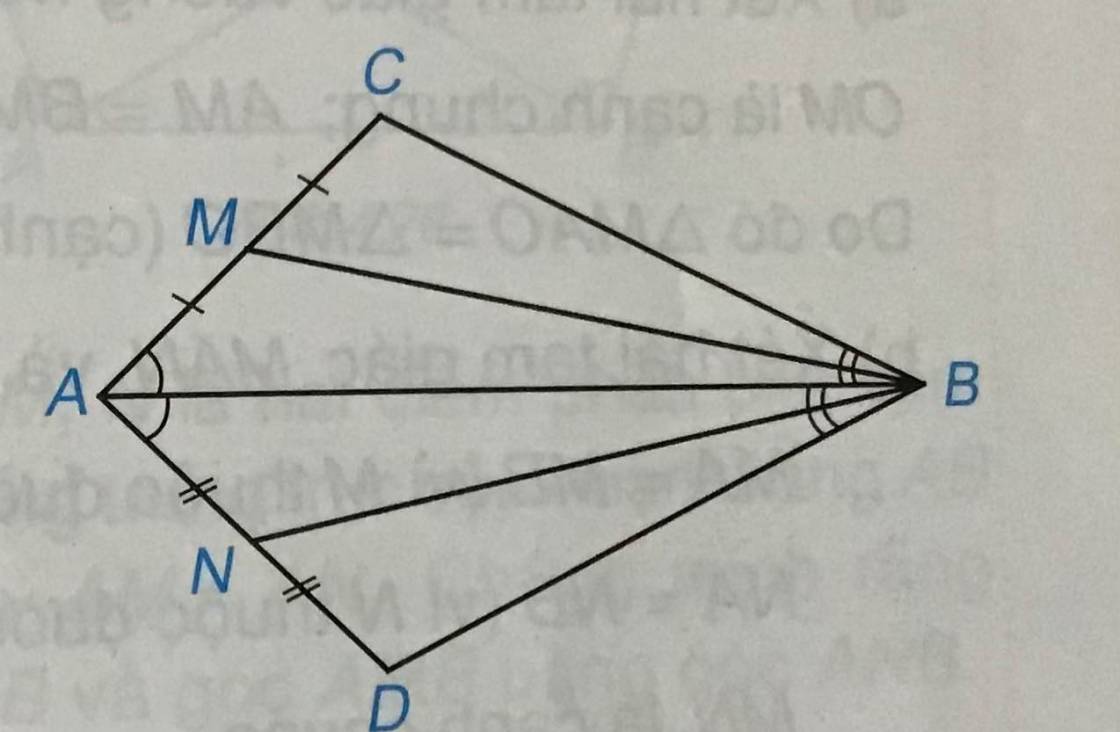
Xét \(\Delta\)ABC  và \(\Delta\) ABD ta có: AB chung;

   góc ABC = góc ABD 

    góc CAB = góc DAB 

⇒ \(\Delta\) ABC = \(\Delta\) ABD (g-c-g)

⇒ BC = BD

    AC = AD

BC = BD ⇒ \(\Delta\) CBD  cân tại B mà AB là phân giác của góc CBD nên 

⇒ AB là trung trực của CD vì trong tam giác cân đường cao cũng là đường trung trực, đường phân giác. 

b, Xét \(\Delta\) ACD có

      AM = AC; 

      AN = ND 

⇒ MN là đường trung bình của tam giác ACD 

 ⇒ MN//CD (đpcm)

c, AC = AD (cmt)

⇒ AN = AM = \(\dfrac{1}{2}AC\)

Xét tam giác AMB và tam giác ANB ta có:

  AB chung;  AN = AM 

 góc NAB = góc BAM 

⇒ \(\Delta\) AMB = \(\Delta\) ANB (c-g-c)

⇒ Góc AMB = góc ANB (đpcm)

Lời giải:

$(3\frac{5}{7}x-1\frac{5}{7}x)-\frac{1}{3}=\frac{2}{3}$

$2x-\frac{1}{3}=\frac{2}{3}$

$2x=\frac{2}{3}+\frac{1}{3}=1$

$x=\frac{1}{2}$

\(x-\dfrac{1}{3}=2-3x\)

\(\Rightarrow x+3x=2+\dfrac{1}{3}\)

\(\Rightarrow4x=\dfrac{7}{3}\)

\(\Rightarrow x=\dfrac{7}{3}:4\)

\(\Rightarrow x=\dfrac{7}{12}\)

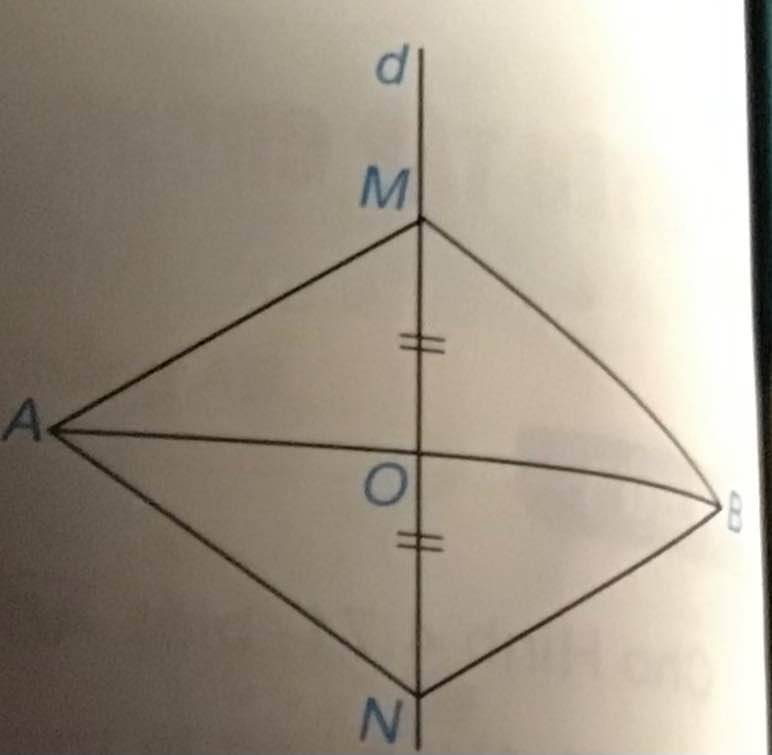
c, BE = EC 

⇒ \(\Delta\) BCE cân tại E

BD = DC 

⇒ DE \(\perp\) BC = D

    AD \(\perp\) BC = D

⇒ A; D; E thẳng hàng vì qua một điểm chỉ kẻ được duy nhất một đường thẳng vuông góc với đường thẳng đã cho.

giúp mik với :(