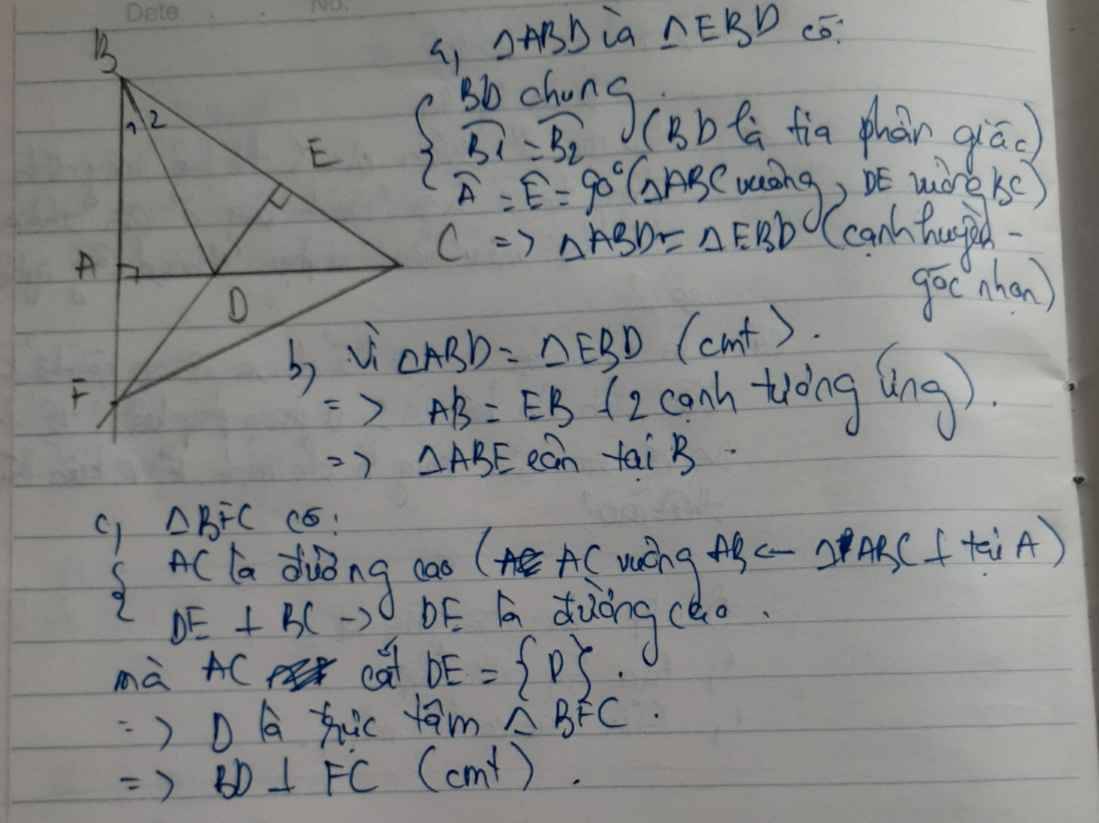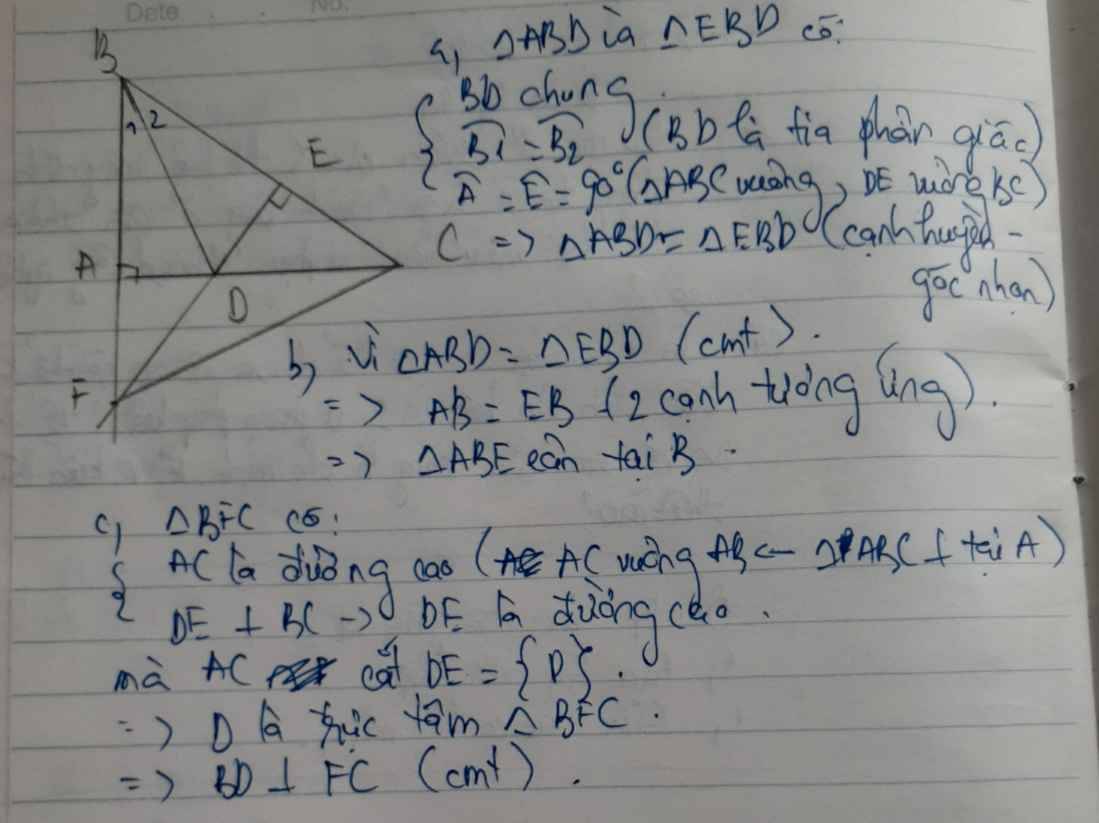Cho tam giác ABC vuông tại A (AB < AC). Kẻ tia phân giác của góc ABC cắt đoạn AC tại D. Từ D kẻ dường thẳng vuông góc với BC cắt BC tại E. Tia BA cắt tia ED tại F.
a) Chứng minh tam giác ABD = tam giác EBD
b) Tam giác ABE là tam giác gì? Vì sao?
c) Chứng minh rằng BD vuông góc với CF
nhanh lên với ạ