Thực hiện phép tính: a,(9/10 - 15/16) X (5/12 - 11/15 - 7/20) b,(-1)3 + (-2/3)2: 2 2/3 + 5/6 c,15 X (-1/5)2 + 1/5 - 2 X (-1/2)3 - 1/2 d,22 - (-5/7) + (1/3)4 X 36
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(x^2.\left(2x-6\right)-2x^2=0\\ \Leftrightarrow2x^2.\left(x-3-1\right)-0\\ \Leftrightarrow2x^2\left(x-4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)

Lời giải:
Giả sử chia 315 thành 3 phần có giá trị là $a,b,c$ tỉ lệ nghịch với $3,5,6$. Theo bài ra ta có:
$a+b+c=315$
$3a=5b=6c=\frac{a}{\frac{1}{3}}=\frac{b}{\frac{1}{5}}=\frac{c}{\frac{1}{6}}$
Áp dụng TCDTSBN:
$3a=5b=6c=\frac{a}{\frac{1}{3}}=\frac{b}{\frac{1}{5}}=\frac{c}{\frac{1}{6}}=\frac{a+b+c}{\frac{1}{3}+\frac{1}{5}+\frac{1}{6}}=\frac{315}{\frac{7}{10}}=450$
$\Rightarrow a=450:3=150; b=450:5=90; c=450:6=90$

Để x + 2y và 2x - y là số hữu tỷ, ta có thể thiết lập hệ phương trình sau:
x + 2y = a/b (1)
2x - y = c/d (2)
Trong đó a, b, c, d là các số nguyên và b, d khác 0.
Từ phương trình (1), ta có x = a/b - 2y. Thay vào phương trình (2), ta có:
2(a/b - 2y) - y = c/d
2a/b - 4y - y = c/d
2a/b - 5y = c/d
Để 2a/b - 5y là số hữu tỷ, ta cần 5y cũng là số hữu tỷ. Vì vậy, y phải là số hữu tỷ.
Tiếp theo, để x = a/b - 2y là số hữu tỷ, ta cần a/b - 2y cũng là số hữu tỷ. Vì y là số hữu tỷ, nên a/b - 2y cũng là số hữu tỷ.
Vậy, nếu x + 2y và 2x - y là số hữu tỷ, thì x và y đều là số hữu tỉ.

Lời giải:
Vì $x,y$ là 2 đại lượng tỉ lệ thuận với nhau nên đặt $y=kx$ với $k$ là hệ số tỉ lệ của $y$ so với $x$.
Thay $x=5; y=-15$ thì:
$-15=k.5\Rightarrow x=-3$
$\Rightarrow y=kx=-3x$
Khi $x=3$ thì $y=-3x=-3.3=-9$
Lời giải:
Vì $x,y$ là 2 đại lượng tỉ lệ thuận với nhau nên đặt $y=kx$ với $k$ là hệ số tỉ lệ của $y$ so với $x$.
Thay $x=5; y=-15$ thì:
$-15=k.5\Rightarrow x=-3$
$\Rightarrow y=kx=-3x$
Khi $x=3$ thì $y=-3x=-3.3=-9$

\(\left|x-\dfrac{1}{2}\right|-1=\dfrac{5}{2}\)
\(\Rightarrow\left|x-\dfrac{1}{2}\right|=\dfrac{5}{2}+1\)
\(\Rightarrow\left|x-\dfrac{1}{2}\right|=\dfrac{7}{2}\)
\(\Rightarrow\left[{}\begin{matrix}x-\dfrac{1}{2}=\dfrac{7}{2}\\x-\dfrac{1}{2}=-\dfrac{7}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=4\\x=-3\end{matrix}\right.\)
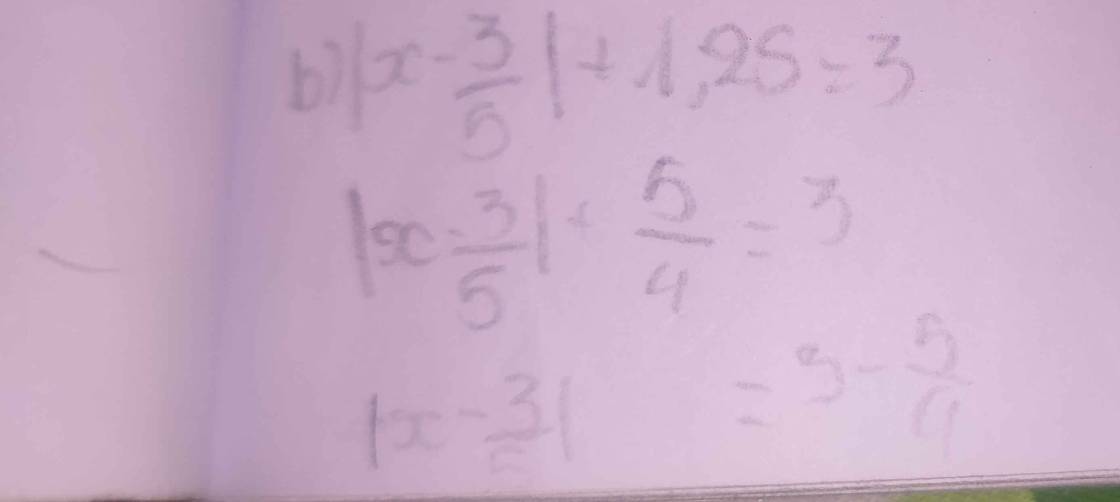
a, (\(\dfrac{9}{10}\) - \(\dfrac{15}{16}\)) \(\times\) ( \(\dfrac{5}{12}\) - \(\dfrac{11}{15}\) - \(\dfrac{7}{20}\))
= (\(\dfrac{72}{80}\) - \(\dfrac{75}{80}\)) \(\times\) (\(\)\(\dfrac{25}{60}\) - \(\dfrac{44}{60}\) - \(\dfrac{21}{60}\))
= - \(\dfrac{3}{80}\) \(\times\) (- \(\dfrac{2}{3}\))
= \(\dfrac{1}{40}\)
b, (-1)3 + (- \(\dfrac{2}{3}\))2 : 2\(\dfrac{2}{3}\) + \(\dfrac{5}{6}\)
= -13 + \(\dfrac{4}{9}\) : \(\dfrac{8}{3}\) + \(\dfrac{5}{6}\)
= -1 + \(\dfrac{4}{9}\) \(\times\) \(\dfrac{3}{8}\) + \(\dfrac{5}{6}\)
= -1 + \(\dfrac{1}{6}\) + \(\dfrac{5}{6}\)
= -1 + 1
= 0