
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Độ dài cạnh phần đất còn lại là 16-x(m)
Diện tích phần đất còn lại là 196m2 nên ta có:
\(\left(16-x\right)^2=196\)
=>\(\left(x-16\right)^2=196\)
=>\(\left[{}\begin{matrix}x-16=14\\x-16=-14\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=30\left(loại\right)\\x=2\left(nhận\right)\end{matrix}\right.\)
Vậy: Độ dài bề rộng là 2m

Nhận thấy \(x_0=0\) không phải là nghiệm của phương trình đã cho.
Giả sử \(x_0< 0\), ta có \(x_0^3-x_0-1=0\)
\(\Leftrightarrow x_0\left(x_0^2-1\right)=1\)
\(\Leftrightarrow x_0\left(x_0-1\right)\left(x_0+1\right)=1\) (*)
Nếu \(x_0\le-1\) thì VT (*) \(\le0< 1=VP\), do đó (*) vô lý.
Xét \(-1< x_0< 0\) thì \(-1< x_0^3< 0\) và \(0< -x_0< 1\)
Do đó \(VT=x_0^3-x_0< 0+1=1=VP\) nên (*) vô lý.
Vậy điều giả sử ban đầu là sai \(\Rightarrow x_0>0\)
Đặt f(x)=x3-x-1
Vì \(f\left(x\right)=x^3-x-1\)
nên hàm số liên tục trên R
\(f\left(1\right)=1^3-1-1=-1;f\left(2\right)=2^3-2-1=5\)
Vì \(f\left(1\right)\cdot f\left(2\right)< 0\)
nên hàm số f(x)=x3-x-1 có nghiệm trên khoảng (1;2)
=>\(x_0\in\left(1;2\right)\)
=>\(x_0>0\)

\(a.\left\{{}\begin{matrix}\left(x+3\right)^2-2y^3=6\\3\left(x+3\right)^2+5y^3=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3\left(x+3\right)^2-6y^3=18\\3\left(x+3\right)^2+5y^3=7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\left(x+3\right)^2-2y^3=6\\11y^3=-11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x+3\right)^2+2=6\\y^3=-1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\left(x+3\right)^2=4\\y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x+3=4\\x+3=-4\end{matrix}\right.\\y=-1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=1\\x=-7\end{matrix}\right.\\y=-1\end{matrix}\right.\)
Vậy: \(\left(x;y\right)=\left\{\left(1;-1\right);\left(-7;-1\right)\right\}\)
\(b.\left\{{}\begin{matrix}x^2+2\left(y^2+2y\right)=10\\3x^2-\left(y^2+2y\right)=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2+2\left(y^2+2y\right)=10\\6x^2-2\left(y^2+2y\right)=18\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x^2+2\left(y^2+2y\right)=10\\7x^2=28\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2+2\left(y^2+2y\right)=10\\x^2=4\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2\left(y^2+2y\right)=6\\x=\pm2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y^2+2y-3=0\\x=\pm2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}y=1\\y=-3\end{matrix}\right.\\x=\pm2\end{matrix}\right.\)
Vậy: \(\left(x;y\right)=\left\{\left(2;1\right);\left(2;-3\right);\left(-2;1\right);\left(-2;-3\right)\right\}\)

\(\left\{{}\begin{matrix}3x+ay=5\\2x+y=b\end{matrix}\right.\)
a) Để hpt có nghiệm duy nhất thì:
\(\dfrac{3}{2}\ne\dfrac{a}{1}\\ \Leftrightarrow a\ne\dfrac{3}{2}\)
b) Để hpt vô nghiệm thì:
\(\dfrac{3}{2}=\dfrac{a}{1}\ne\dfrac{5}{b}\\ < =>\left\{{}\begin{matrix}a=\dfrac{3}{2}\\\dfrac{3}{2}\ne\dfrac{5}{b}\end{matrix}\right.\\ < =>\left\{{}\begin{matrix}a=\dfrac{3}{2}\\b\ne\dfrac{10}{3}\end{matrix}\right.\)
c) Để hpt vô số nghiệm thì:
\(\dfrac{3}{2}=\dfrac{a}{1}=\dfrac{5}{b}\\ =>\left\{{}\begin{matrix}a=\dfrac{3}{2}\\\dfrac{5}{b}=\dfrac{3}{2}\end{matrix}\right.\\ < =>\left\{{}\begin{matrix}a=\dfrac{3}{2}\\b=\dfrac{10}{3}\end{matrix}\right.\)

\(a.A=\left(\dfrac{1}{1-x}+\dfrac{2}{x+1}-\dfrac{5-x}{1-x^2}\right):\dfrac{1-2x}{x^2-1}\left(x\ne\pm1;x\ne\dfrac{1}{2}\right)\\=\left[\dfrac{1+x}{\left(1-x\right)\left(1+x\right)}+\dfrac{2\left(1-x\right)}{\left(1-x\right)\left(1+x\right)}-\dfrac{5-x}{\left(1-x\right)\left(1+x\right)}\right]\cdot\dfrac{x^2-1}{1-2x}\\ =\dfrac{1+x+2-2x-5+x}{\left(1-x\right)\left(1+x\right)}\cdot\dfrac{x^2-1}{1-2x}\\ =\dfrac{-2}{\left(1-x\right)\left(1+x\right)}\cdot\dfrac{x^2-1}{1-2x}\\ =\dfrac{2}{\left(x+1\right)\left(x-1\right)}\cdot\dfrac{\left(x+1\right)\left(x-1\right)}{1-2x}\\ =\dfrac{2}{1-2x}\)
b) Để A nguyên thì 2 ⋮ 1 - 2x
Mà: 1 - 2x lẻ với mọi x nguyên
=> \(1-2x\in\left\{1;-1\right\}\)
=> \(2x\in\left\{0;2\right\}\)
=> \(x\in\left\{0;1\right\}\)
Kết hợp với đk => x = 0
c) Để \(\left|A\right|=A\Rightarrow A\ge0\)
\(=>\dfrac{2}{1-2x}\ge0\\ =>1-2x>0\\ =>2x< 1\\ =>x< \dfrac{1}{2}\)
Kết hợp với đk `=>x<1/2;x≠-1`

Lời giải:
Đặt $\frac{1}{x-1}=a; \frac{1}{y+2}=b$ thì HPT trở thành:
\(\left\{\begin{matrix} 2a+b=2\\ 8a-3b=1\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} b=2-2a\\ 8a-3b=1\end{matrix}\right.\Rightarrow 8a-3(2-2a)=1\)
$\Leftrightarrow 8a-6+6a=1$
$\Leftrightarrow 14a=7\Leftrightarrow a=\frac{1}{2}$
$b=2-2a=2-2.\frac{1}{2}=1$
Vậy $\frac{1}{x-1}=\frac{1}{2}; \frac{1}{y+2}=1$
$\Leftrightarrow x-1=2; y+2=1$
$\Leftrightarrow x=3; y=-1$
ĐK \(\left\{{}\begin{matrix}x\ne1\\y\ne-2\end{matrix}\right.\)
Đặt \(a=\dfrac{1}{x-1};b=\dfrac{1}{y+2}\left(a\ne0;b\ne0\right)\)
Hệ phương trình trở thành \(\left\{{}\begin{matrix}2a+b=2\\8a-3b=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=2-2a\\8a-3.\left(2-2a\right)=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}b=2-2a\\14a-6=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}b=2-2a\\14a=7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}b=2-2.0,5\\a=0,5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}b=1\\a=0,5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}a=0,5\\b=1\end{matrix}\right.\)
- \(a=0,5\Rightarrow\dfrac{1}{x-1}=0,5\Rightarrow x-1=2\Rightarrow x=3\left(tm\right)\)
- \(b=1\Rightarrow\dfrac{1}{y+2}=1\Rightarrow y+2=1\Rightarrow y=-1\left(tm\right)\)
Vậy hệ phương trình có nghiệm x = 3 và y = -1

a: Xét tứ giác BFHD có \(\widehat{BFH}+\widehat{BDH}=90^0+90^0=180^0\)
nên BFHD là tứ giác nội tiếp
Xét tứ giác AFDC có \(\widehat{AFC}=\widehat{ADC}=90^0\)
nên AFDC là tứ giác nội tiếp
b: Xét (O) có
\(\widehat{BAC}\) là góc nội tiếp chắn cung BC
Do đó: \(\widehat{BOC}=2\cdot\widehat{BAC}=120^0\)
Độ dài cung nhỏ BC là:
\(l=\dfrac{\Omega\cdot R\cdot n}{180}=\dfrac{\Omega\cdot4\cdot120}{180}=\Omega\cdot\dfrac{8}{3}\)
c: Xét tứ giác CEHD có \(\widehat{CEH}+\widehat{CDH}=90^0+90^0=180^0\)
nên CEHD là tứ giác nội tiếp
Ta có: \(\widehat{FDH}=\widehat{FBH}\)(BFHD nội tiếp)
\(\widehat{EDH}=\widehat{ECH}\)(CEHD nội tiếp)
mà \(\widehat{FBH}=\widehat{ECH}\left(=90^0-\widehat{BAC}\right)\)
nên \(\widehat{FDH}=\widehat{EDH}\)
=>DA là phân giác của góc FDE

Bài 5:
Gọi giá tiền mỗi chiếc áo bạn Hoa đã mua là x(nghìn đồng)
(Điều kiện: x>0)
Giá tiền ban đầu của mỗi chiếc áo là x+30(nghìn đồng)
Số lượng áo dự định là \(\dfrac{600}{x+30}\)(cái)
Số lượng áo thực tế là \(\dfrac{600}{x}\)(cái)
Vì số lượng áo thực tế mua được bằng 1,25 lần số lượng áo ban đầu định mua thì \(\dfrac{600}{x}=1,25\cdot\dfrac{600}{x+30}\)
=>\(\dfrac{600}{x}=\dfrac{750}{x+30}\)
=>\(\dfrac{4}{x}=\dfrac{5}{x+30}\)
=>5x=4x+120
=>x=120(nhận)
Vậy: Giá tiền của mỗi chiếc áo thực tế là 120 nghìn đồng

Gọi chiều rộng mảnh đất là x(m)
(Điều kiện: x>0)
Chiều dài mảnh đất là x+30(m)
Chiều rộng mảnh đất khi tăng thêm 10m là x+10(m)
Chiều dài mảnh đất khi giảm 15m là x+30-15=x+15(m)
Mảnh đất có chu vi là 210m nên 2(x+10+x+15)=210
=>2x+25=105
=>2x=105-25=90
=>x=45(nhận)
Vậy: Chiều rộng mảnh đất là 45m
Chiều dài mảnh đất là 45+30=75m
c dài là a
c rộng là b
+) a=b+30
+) (b+10) + (a-15) = 210 : 2
giải hệ pt suy ra a=70 và b=40
LIKE CHO TUI NHAA PLSS

 giúp tui zoiiii
giúp tui zoiiii 
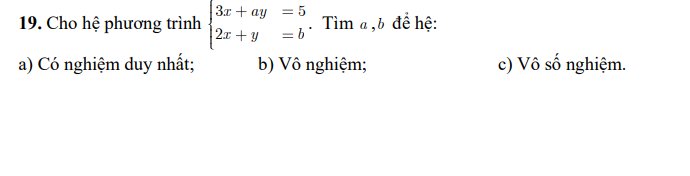
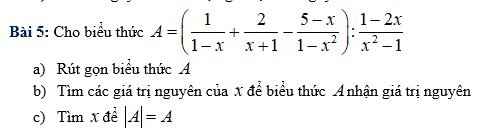
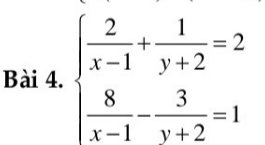


Gọi vận tốc lúc đi là x(km/h)
(Điều kiện: x>0)
Vận tốc lúc về là x+10(km/h)
Thời gian đi là \(\dfrac{150}{x}\left(giờ\right)\)
Thời gian về là \(\dfrac{150}{x+10}\left(giờ\right)\)
Tổng thời gian cả đi lẫn về là 5h30p=5,5 giờ nên ta có:
\(\dfrac{150}{x}+\dfrac{150}{x+10}=5,5\)
=>\(\dfrac{1}{x}+\dfrac{1}{x+10}=\dfrac{150}{5,5}=\dfrac{300}{11}\)
=>\(\dfrac{x+10+x}{x\left(x+10\right)}=\dfrac{300}{11}\)
=>300x(x+10)=11(2x+10)
=>\(300x^2+3000x-22x-110=0\)
=>\(300x^2+2978x-110=0\)(1)
\(\text{Δ}=2978^2-4\cdot300\cdot\left(-110\right)=9000484>0\)
Do đó: Phương trình (1) có hai nghiệm phân biệt là:
\(\left[{}\begin{matrix}x=\dfrac{-2978-\sqrt{9000484}}{600}\left(loại\right)\\x=\dfrac{-2978+\sqrt{9000484}}{600}\left(nhận\right)\end{matrix}\right.\)
Vậy: Vận tốc lúc đi là \(\dfrac{-2978+\sqrt{9000484}}{600}\left(\dfrac{km}{h}\right)\)