hộ e cái mọi người ơi

Lời giải:
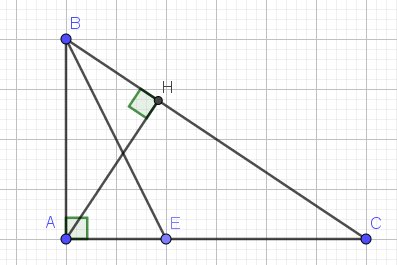
Áp dụng định lý Pitago:

$BC=\sqrt{AB^2+AC^2}=\sqrt{5^2+12^2}=13$ (cm)

Xét tam giác $BAH$ và $BCA$ có:
$\widehat{B}$ chung

$\widehat{BHA}=\widehat{BAC}=90^0$

$\Rightarrow \triangle BAH\sim \triangle BCA$ (g.g)

$\Rightarrow \frac{BA}{BH}=\frac{BC}{BA}$

$\Rightarrow AB^2=BH.BC$ 

Theo tính chất về tia phân giác ta có:

$\frac{AE}{EC}=\frac{AB}{BC}=\frac{5}{13}$

$\Rightarrow \frac{AE}{AC}=\frac{5}{18}$
$\Rightarrow AE=\frac{5}{18}.AC=\frac{5}{18}.12=\frac{10}{3}$ (cm)

$CE=AC-AE=12-\frac{10}{3}=\frac{26}{3}$ (cm)

Hình vẽ:

Nhớ tick cho mình nha

\(\dfrac{1}{3}\)x² + \(\dfrac{1}{x^2}\) - 8x + 32 = \(\dfrac{1}{x^2}\) - 2x + 8  ĐK: x ≠ 0

⇔\(\dfrac{1}{3}\)x² + \(\dfrac{1}{x^2}\) - \(\dfrac{1}{x^2}\) - 8x + 2x + 32 - 8 = 0

⇔\(\dfrac{1}{3}\)x² - 6x +24 = 0

⇔\(\left(x-12\right)\) \(\left(x-6\right)\) = 0

⇔\(\left[{}\begin{matrix}x-12=0\\x-6=0\end{matrix}\right.\)

⇔\(\left[{}\begin{matrix}x=12\left(tm\right)\\x=6\left(tm\right)\end{matrix}\right.\)

⇒ S = \(\left\{12;6\right\}\)

?

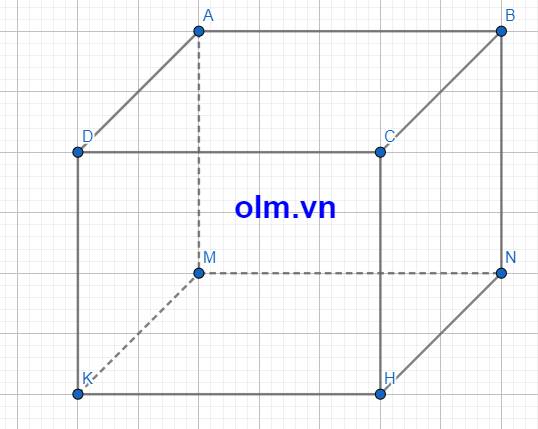
Vì diện tích mặt bên gắn với chiều rộng là 12 cm² nên diện tích mặt bên đó bằng chiều rộng nhân với chiều cao.

Từ lập luận trên ta có:

Chiều rộng của hình hộp chữ nhật là: 

12 : 4 = 3 (cm)

Thể tích của hình hộp chữ nhật là:

5 \(\times\) 3 \(\times\) 4 = 60 (cm³)

Diện tích xung quanh của hình hộp chữ nhật là:

( 5 + 3) \(\times\) 2 \(\times\) 4 = 64 (cm²)

Diện tích hai mặt đáy của hình hộp chữ nhật là:

5 \(\times\) 3 \(\times\) 2 = 30 (cm²)

Diện tích toàn phần của hình hộp chữ nhật là:

64 + 30 = 94 (cm²)

Kết luận: Thể tích hình hộp chữ nhật 60 cm³

               Diện tích toàn phần của hình hộp chữ nhật là: 94 cm²

- Dễ dàng nhận thấy \(x=-1\) không phải là 1 nghiệm của đa thức P(x).

- Gọi b là 1 nghiệm của đa thức \(P\left(x\right)=x^3+3x^2-1\)

Do đó: \(b^3+3b^2-1=0\)

\(\Rightarrow\left(b^3+3b^2+3b+1\right)-3\left(b+1\right)+1=0\)

\(\Rightarrow\left(b+1\right)^3-3\left(b+1\right)+1=0\)

\(\Rightarrow\dfrac{\left(b+1\right)^3-3\left(b+1\right)+1}{\left(b+1\right)^3}=0\)

\(\Rightarrow\left(\dfrac{1}{b+1}\right)^3-3.\left(\dfrac{1}{b+1}\right)^2+1=0\)

\(\Rightarrow\left(-\dfrac{1}{b+1}\right)^3+3.\left(-\dfrac{1}{b+1}\right)^2-1=0\)

Thay \(x=-\dfrac{1}{b+1}\) vào \(P\left(x\right)=x^3+3x^2-1\) ta được:

\(P\left(-\dfrac{1}{b+1}\right)=\left(-\dfrac{1}{b+1}\right)^3+3.\left(-\dfrac{1}{b+1}\right)^2-1=0\)

\(\Rightarrow-\dfrac{1}{b+1}\) là một nghiệm của đa thức P(x).

Đặt \(a=-\dfrac{1}{b+1}\Rightarrow ab+a+1=0\) \(\Rightarrowđpcm\)