Bài 5. (1,0 điểm) Cho tam giác $ABC$, trung tuyến $AM$, đường phân giác của góc $AMB$ cắt $AB$ tại $D$. Cho $BC=30$ cm; $A D=6$ cm; $A B=10$ cm. Tính độ dài $A M$.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


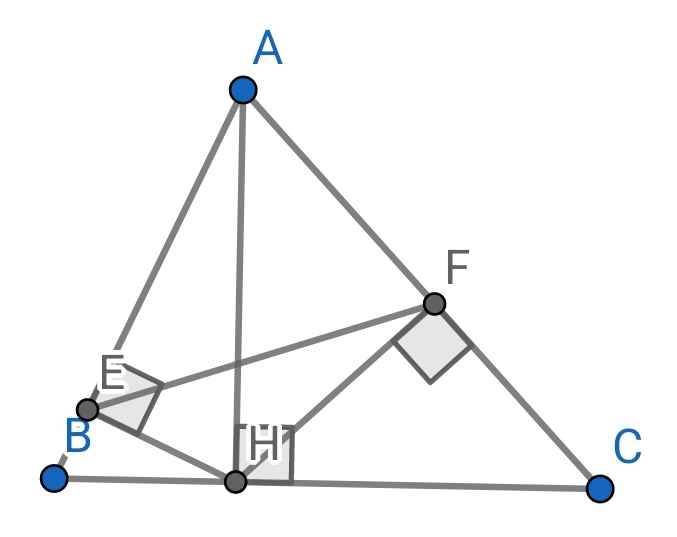
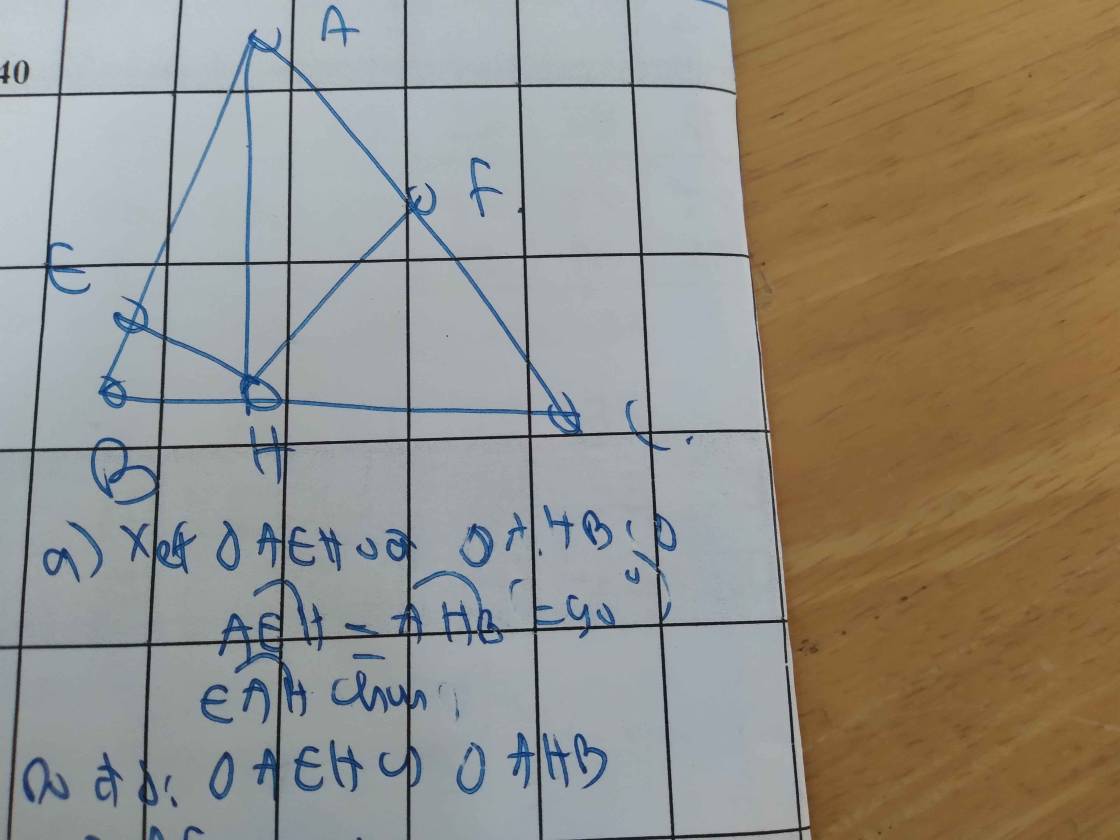
a) Xét hai tam giác vuông: ∆AEH và ∆AHB có:
∠A chung
⇒ ∆AEH ∽ ∆AHB (g-g)
⇒ AH/AB = AE/AH
⇒ AH² = AE.AB
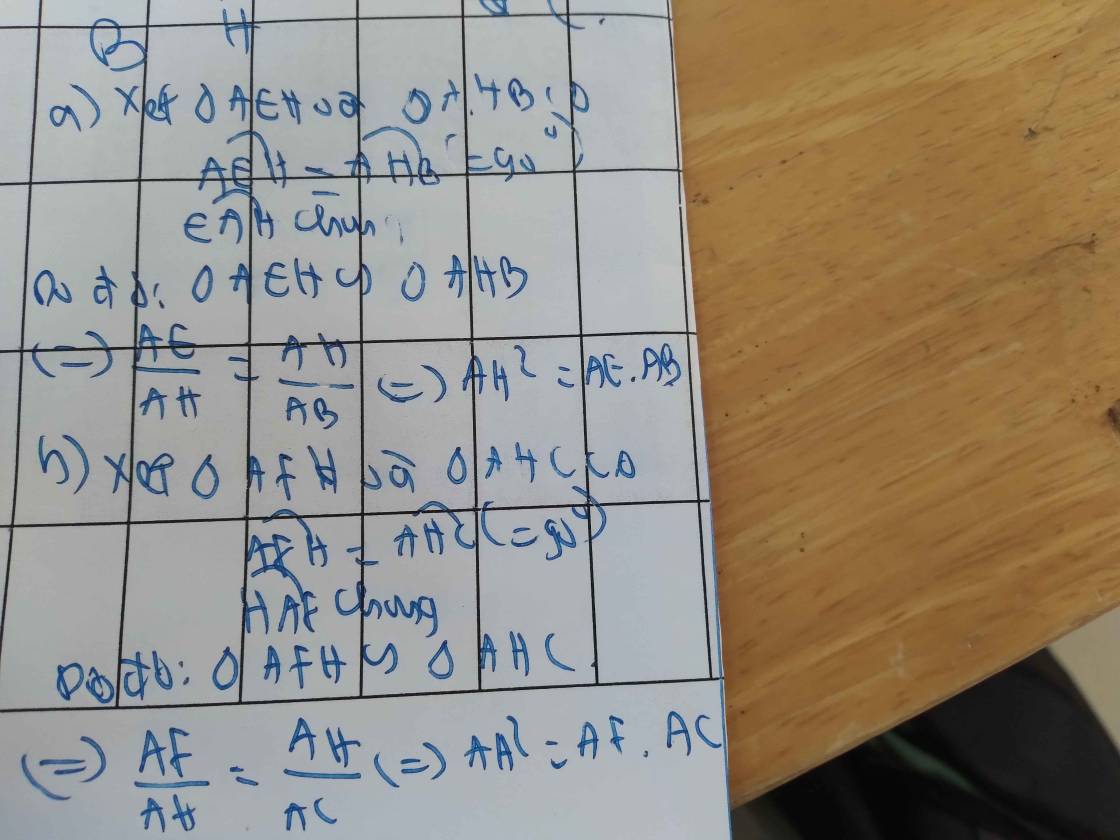
b) Xét hai tam giác vuông: ∆AFH và ∆AHC có:
∠A chung
⇒ ∆AFH ∽ ∆AHC (g-g)
⇒ AH/AC = AF/AH
⇒ AH² = AF.AC
Mà AH² = AE.AB (cmt)
⇒ AE.AB = AF.AC
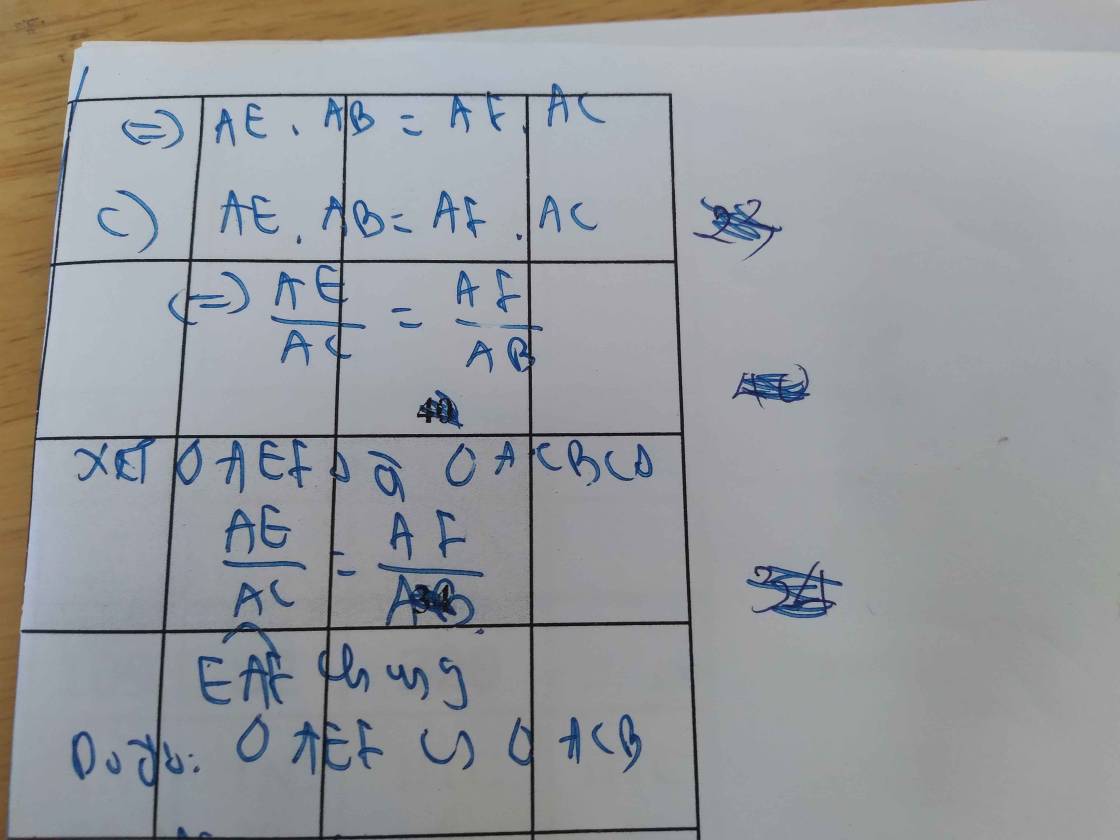
c) Do AE.AB = AF.AC (cmt)
⇒ AE/AC = AF/AB
Xét ∆AEF và ∆ACB có:
AE/AC = AF/AB (cmt)
∠A chung
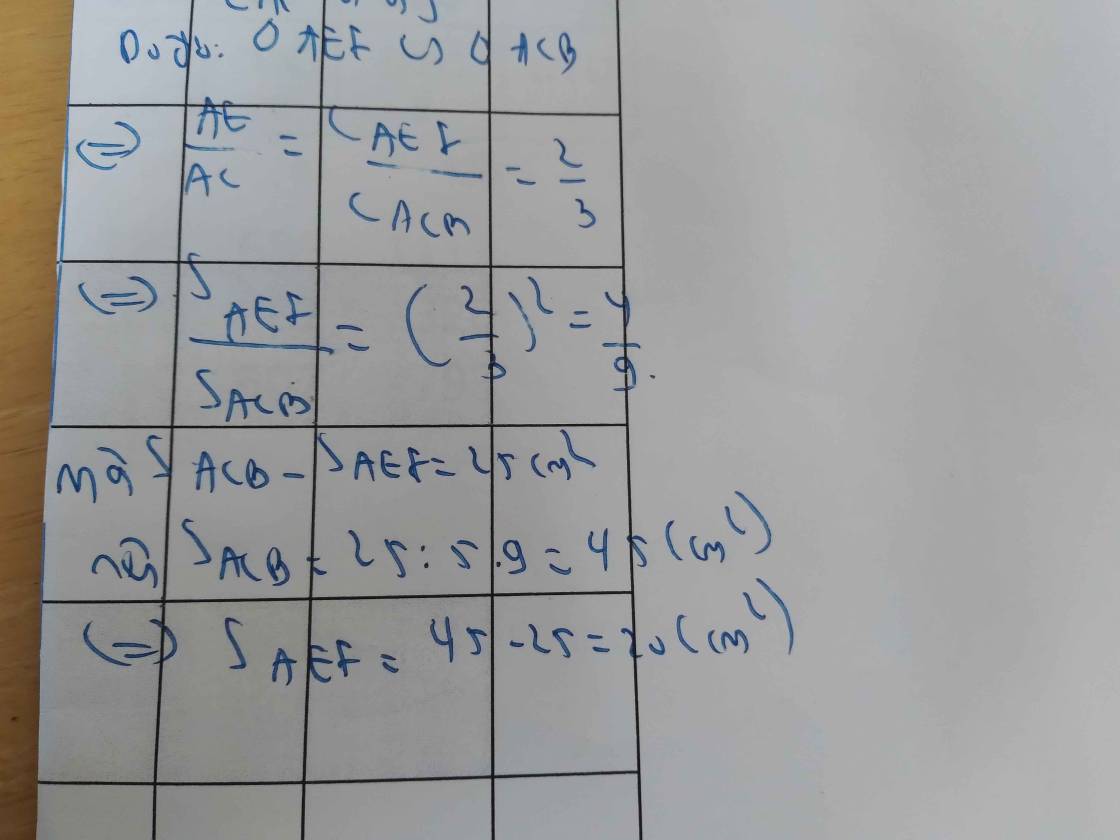
⇒ ∆AEF ∽ ∆ACB (c-g-c)
Gọi p và p' lần lượt là chu vi của ∆AEF và ∆ACB
⇒ p/p' = 20/30= 2/3
Do ∆AEF ∽ ∆ACB (cmt)
⇒ AE/AC = AF/AB = EF/BC = p/p' = 2/3
Gọi x, y lần lượt là diện tích của ∆AEF và ∆ACB
Do ∆AEF ∽ ∆ACB (cmt)
⇒ x/y = (2/3)² = 4/9
⇒ x/4 = y/9
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
x/4 = y/9 = (y - x)/(9 - 4) = 25/5 = 5
x/4 = 5 ⇒ x = 5.4 = 20 (cm²)
y/9 = 5 ⇒ y = 5.9 = 45 (cm²)
Vậy diện tích ∆AEF là 20 cm², diện tích ∆ACB là 45 cm²

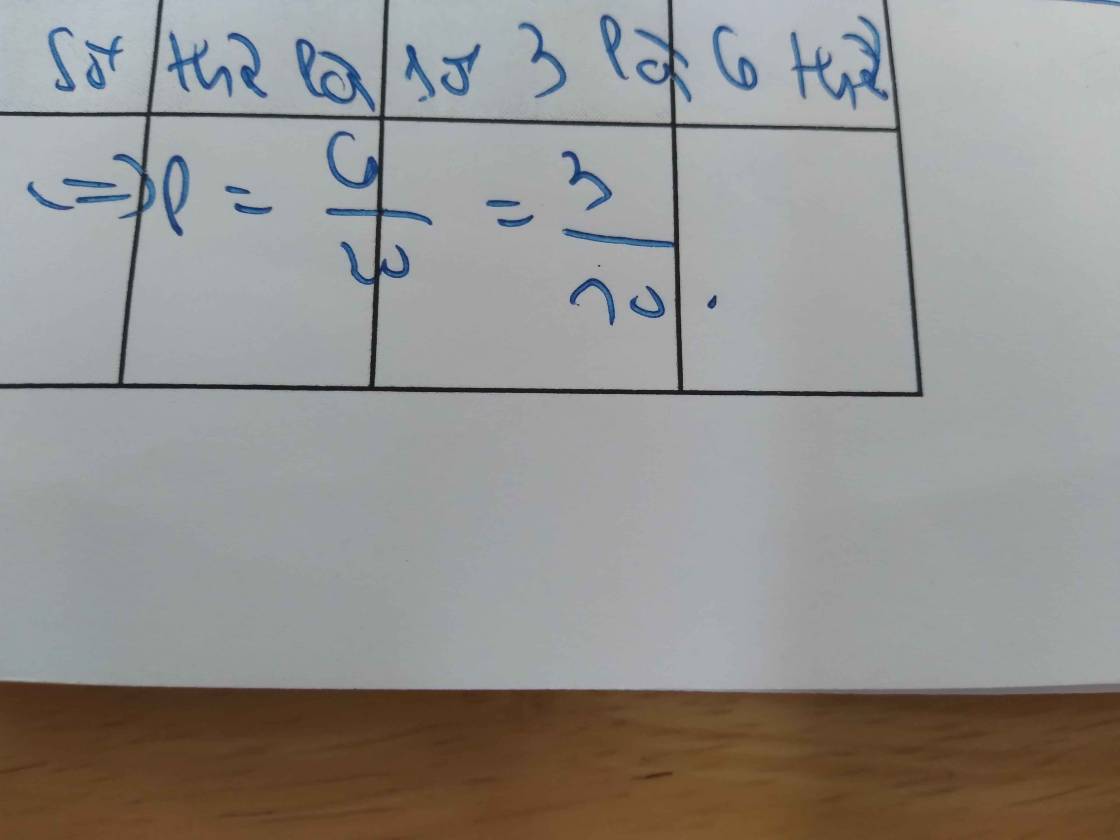
Có 6 khả năng rút được thẻ số 3 nên xác suất của biến cố "Thẻ rút ra là thẻ đánh số 3" là:
P = 6/20 = 3/10

Giải:
Đổi 1 giờ 30 phút = 1,5 giờ
Cứ một giờ ca nô xuôi dòng được: 1 : 1,5 = \(\dfrac{2}{3}\)(quãng sông AB)
Cứ một giờ ca nô ngược dòng được: 1 : 2 = \(\dfrac{1}{2}\) (quãng sông AB)
Cứ một giờ dòng nước chảy được: (\(\dfrac{2}{3}\) - \(\dfrac{1}{2}\)) : 2 = \(\dfrac{1}{12}\)(quãng sông AB)
Quãng sông AB dài là: 3 : \(\dfrac{1}{12}\) = 36 (km)
Vận tốc ca nô khi ngược dòng là: 36 : 2 = 18 (km/h)
Vận tốc riêng của ca nô là: 18 + 3 = 21 (km/h)
Kết luận: Quãng sông AB dài 36 km
Vận tốc riêng của ca nô là 21 km/h
Gọi x (km/h) là vận tốc riêng của ca nô (x > 3)
Vận tốc đi xuôi dòng từ A đến B: x + 3 (km/h)
1 giờ 30 phút = 1,5 giờ
Quãng đường đi xuôi dòng: (x + 3).1,5 (km)
Vận tốc đi ngược dòng từ B về A: x - 3 (km/h)
Quãng đường đi ngược dòng: (x - 3).2 (km)
Do đi cùng một quãng đường AB nên ta có phương trình:
(x + 3).1,5 = (x - 3).2
1,5x + 4,5 = 2x - 6
2x - 1,5x = 4,5 + 6
0,5x = 10,5
x = 10,5 : 0,5
x = 21 (nhận)
Vậy vận tốc riêng của ca nô là 21 km/h

a) 3x - 4 = 5 + x
3x - 2x = 5 + 4
x = 9
Vậy S = {9}
b) 3(x - 1) - 7 = 5(x + 2)
3x - 3 - 7 = 5x + 10
3x - 10 = 5x + 10
3x - 5x = 10 + 10
-2x = 20
x = 20 : (-2)
x = -10
Vậy S = {-10}

(x - a)/bc + (x - b)/ca + (x - c)/ab = 2/a + 2/b + 2/c
a(x - a) + b(x - b) + c(x - c) = 2bc + 2ac + 2ab
ax - a² + bx - b² + cx - c² = 2bc + 2ac + 2ab
(a + b + c)x = a² + b² + c² + 2bc + 2ac + 2ab
(a + b + c)x = (a + b + c)²
x = (a + b + c)²/(a + b + c)
x = a + b + c
Vậy S = {a + b + c}
Ta có:
Điều kiện xác định:
Khi đó:
+ Nếu thì phương trình có vô số nghiệm.
+ Nếu thì phương trình có nghiệm duy nhất .

a) Với , hàm số trở thành .
Xét hàm số :
Thay thì .
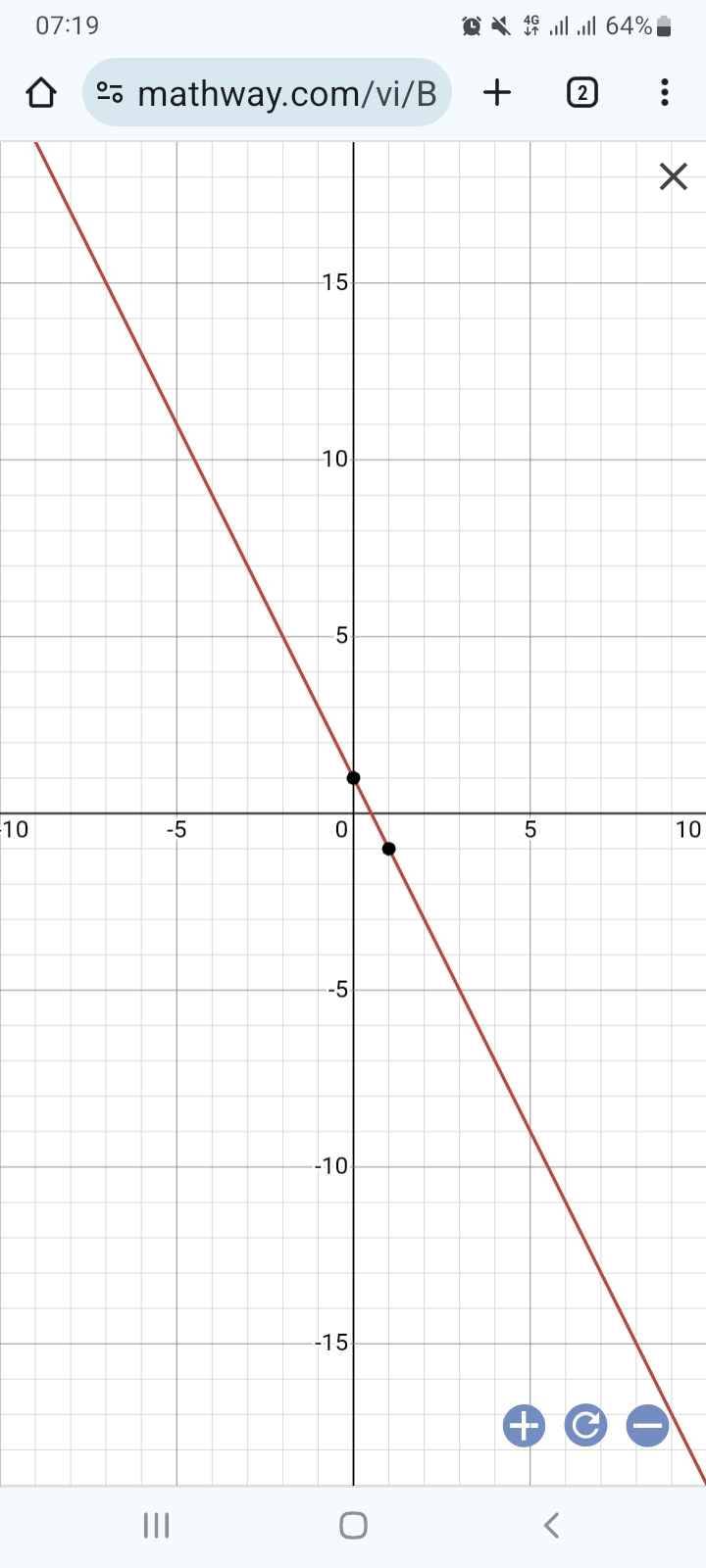
Suy ra đồ thị hàm số đi qua điểm có tọa độ .
Thay thì .
Vì đường thẳng song song với đường thẳng nên: .
Khi đó ta có: và .
Vì đường thẳng đi qua nên:
Suy ra (thoả mãn)
Vậy đường thẳng cần tìm là .
Suy ra đồ thị hàm số đi qua điểm có tọa độ .
Vẽ đồ thị:
Vì đường thẳng song song với đường thẳng nên: .
Khi đó ta có: và .
Vì đường thẳng đi qua nên:
Suy ra (thoả mãn)
Vậy đường thẳng cần tìm là .

Gọi x (h) là thời gian người đó đi từ thành phố về quê (x > 0)
20 phút = 1/3 h
Thời gian người đó đi từ quê lên thành phố là: x + 1/3 (h)
Quãng đường đi từ thành phố về quê: 30x (km)
Quãng đường đi từ quê lên thành phố: 25(x + 1/3) (km)
Theo đề bài, ta có phương trình:
30x = 25(x + 1/3)
30x = 25x + 25/3
30x - 25x = 25/3
5x = 25/3
x = 25/3 : 5
x = 5/3 (nhận)
Vậy quãng đường từ thành phố về quê là: 30 . 5/3 = 50 km

a) 3x - 5 = 4
3x = 4 + 5
3x = 9
x = 9 : 3
x = 3
Vậy S = {3}
b) 2x/3 + (3x - 1)/6 = x/2
4x + 3x - 1 = 3x
7x - 3x = 1
4x = 1
x = 1/4
Vậy S = {1/4}








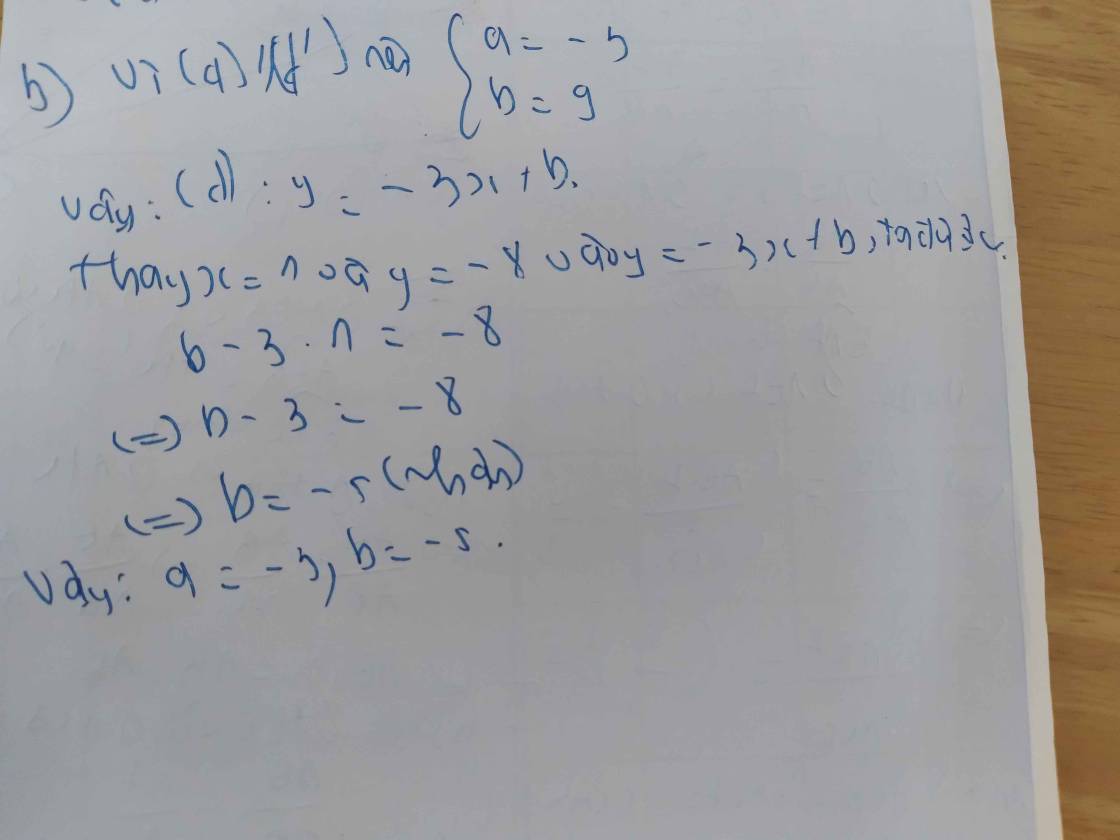

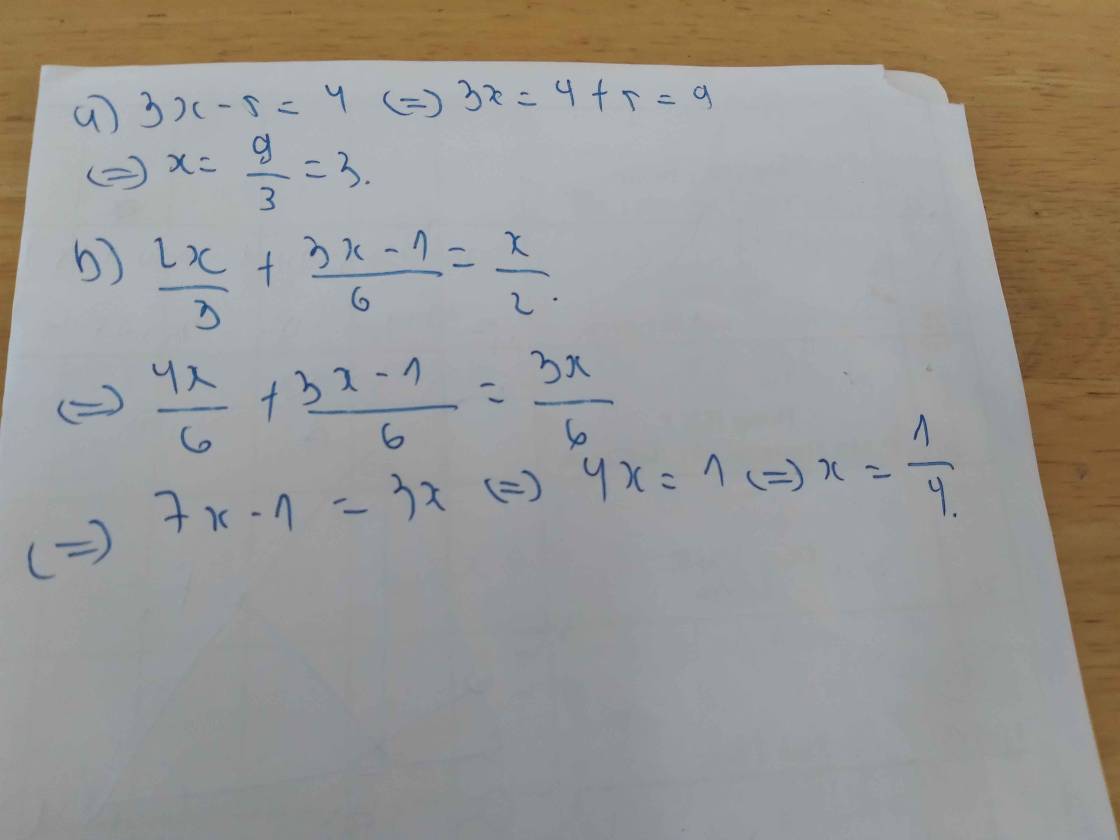
Do M là trung điểm của BC (gt)
⇒ BM = BC : 2 = 30 : 2 = 15 (cm)
BD = AB - AD = 10 - 6 = 4 (cm)
Do MD là đường phân giác của ∆AMB (gt)
⇒ AD/BD = AM/BM
⇒ AM = AD . BM : BD
= 6 . 15 : 4
= 22,5 (cm)
Ta có: 𝐴𝐵=𝐴𝐷+𝐷𝐵AB=AD+DB
Suy ra 𝐷𝐵=𝐴𝐵−𝐴𝐷=10−6=4DB=AB−AD=10−6=4 cm
𝐴𝑀AM là trung tuyến của Δ𝐴𝐵𝐶ΔABC suy ra 𝑀M là trung điểm của 𝐵𝐶BC
Suy ra 𝐵𝑀=𝐶𝑀=12𝐵𝐶=15BM=CM=21BC=15 cm.
Xét Δ𝐴𝐵𝑀ΔABM có 𝑀𝐷MD là phân giác của góc 𝐴𝑀𝐵AMB nên
𝐴𝑀𝐵𝑀=𝐴𝐷𝐷𝐵BMAM=DBAD
𝐴𝑀𝐵𝑀=64=32BMAM=46=23
Do đó 𝐴𝑀=32.𝐵𝑀=32.15=22,5AM=23.BM=23.15=22,5 (cm).