a) Nhận thấy \(\widehat{OBA}=\widehat{OCA}=90^o\) nên tứ giác ABOC nội tiếp đường tròn đường kính OA.

b) Nhân thấy \(\widehat{OID}=\widehat{OBD}=90^o\) nên tứ giác OIBD nội tiếp đường tròn đường kính OD \(\Rightarrow\widehat{IDO}=\widehat{IBO}\)

 Lại có \(\widehat{IBO}=\widehat{CBO}=\widehat{BCO}\) nên dễ dàng suy ra đpcm.

c) Dễ chứng minh tứ giác OCFI nội tiếp \(\Rightarrow\widehat{OCB}=\widehat{OCI}=\widehat{OFI}=\widehat{OFD}\) 

Theo câu b, ta có \(\widehat{FDO}=\widehat{IDO}=\widehat{BCO}\) nên dẫn đến \(\widehat{OFD}=\widehat{FDO}\). Do đó tam giác ODF cân tại O. (đpcm)

d) Tam giác ODF cân tại F có đường cao OI nên I là trung điểm DF.

Mặt khác, có I là trung điểm BE nên tứ giác BDEF là hình bình hành.

\(\Rightarrow\) EF//BD hay EF//AB.

Lại có E là trung điểm BC nên F là trung điểm AC (đpcm)

1,559

a) Thể tích hồ bơi:

12,5 . 5 . 2,5 = 156,25 (m³)

b) Diện tích đáy hồ bơi:

12,5 . 5 = 62,5 (m²)

Diện tích xung quanh hồ bơi:

(12,5 + 5) . 2 . 2,5 = 87,5 (m²)

Diện tích cần lát gạch:

87,5 + 62,5 = 150 (m²)

c) Thể tích nước trong hồ bơi:

12,5 . 5 . 1,5 = 93,75 (m³)

Lời giải:

Đặt $\frac{x}{5}=\frac{y}{-3}=\frac{z}{2}=k\Rightarrow x=5k; y=-3k; z=2k$
Khi đó:

$x+2y-3z=10$

$\Rightarrow 5k+2(-3k)-3(2k)=10$

$\Rightarrow 5k-6k-6k=10$

$\Rightarrow -7k=10\Rightarrow k=\frac{-10}{7}$

$x=5k=\frac{-50}{7}; y=-3k=\frac{30}{7}; z=2k=\frac{-20}{7}$

Lời giải:

Gọi số tự nhiên cần tìm là $a$

$a\vdots 5,7,9$

$\Rightarrow a=BC(5,7,9)$

$\Rightarrow a\vdots BCNN(5,7,9)$

$\Rightarrow a\vdots 315$

Vậy $a=315k$ với $k$ là stn.

Vì $a$ có 4 chữ số nên $315k< 10000$

$\Rightarrow k< 31,7$

Để $a$ lớn nhất thì $k$ lớn nhất

$\Rightarrow k=31$

$a=315.31=9756$

a ⋮ 5; 7; 9 ⇒ a \(\in\) BC(5; 7;9) 

5= 5; 7 = 7; 9 =3² ⇒ BCNN(5; 7; 9) = 3².5.7 = 315

a   \(\in\) BC(315) = {0; 315; 630;1890;...;9765;10080}

Vì a là số tự nhiên lớn nhất có 4 chữ số nên a = 9765

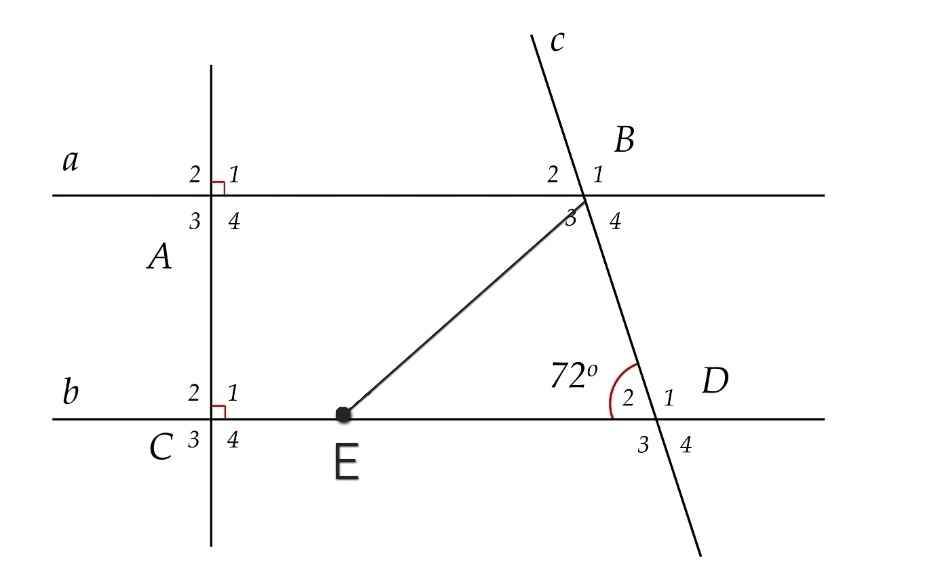 a) Ta có:

∠A₁ = ∠C₁ = 90⁰

Mà ∠A₁ và ∠C₁ là hai góc đồng vị

⇒ a // b

b) Ta có:

∠D₁ + ∠D₂ = 180⁰ (kề bù)

⇒ ∠D₁ = 180⁰ - ∠D₂

= 180⁰ - 72⁰

= 108⁰

Do a // b (cmt)

⇒ ∠ABD = ∠D₁ = 108⁰ (so le trong)

c) Do BE là tia phân giác của ∠ABD

⇒ ∠ABE = ∠ABD : 2

= 108⁰ : 2

= 54⁰

1) -x - 3 = 7

-x = 7 + 3

-x = 10

x = -10

2) x + 5 = -10

x = -10 - 5

x = -15

3) 2x - 7 = 713

2x = 713 + 7

2x = 720

x = 720 : 2

x = 360

4) -129 - (35 - x) = 55

35 - x = -129 - 55

35 - x = -184

x = 35 - (-184)

x = 219

5) 103 - x = 16 - (13 - 8)

103 - x = 16 - 5

103 - x = 11

x = 103 - 11

x = 192

\(\left(12+x\right)-\left(22+x\right)\)

\(=12+x-22-x\)

\(=-10\)

Vậy giá trị của biểu thức đã cho là \(-10\) với mọi \(x\)

\(\dfrac{2}{3}-\left|x-2,4\right|=\dfrac{1}{2}\)

\(\left|x-2,4\right|=\dfrac{2}{3}-\dfrac{1}{2}\)

\(\left|x-2,4\right|=\dfrac{1}{6}\)

*) Với \(x\ge2,4\) ta có:

\(x-2,4=\dfrac{1}{6}\)

\(x=\dfrac{1}{6}+2,4\)

\(x=\dfrac{77}{30}\) (nhận)

*) Với \(x< 2,4\) ta có:

\(x-2,4=-\dfrac{1}{6}\)

\(x=-\dfrac{1}{6}+2,4\)

\(x=\dfrac{67}{30}\) (nhận)

Vậy \(x=\dfrac{67}{30};x=\dfrac{77}{30}\)