viết biểu thức sau dưới dạng lũy thừa 9.3 mũ 2 .1/81.27
cách chình bầyHãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Sửa đề:
\(H=\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}+\dfrac{1}{72}+\dfrac{1}{90}\\ H=\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+\dfrac{1}{4\cdot5}+\dfrac{1}{5\cdot6}+\dfrac{1}{6\cdot7}+\dfrac{1}{7\cdot8}+\dfrac{1}{8\cdot9}+\dfrac{1}{9\cdot10}\\ H=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{10}\\ H=\dfrac{1}{2}-\dfrac{1}{10}\\ H=\dfrac{2}{5}\)
Vậy \(H=\dfrac{2}{5}\)
\(H=\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{72}+\dfrac{1}{90}\)
\(H=\dfrac{1}{90}+\left(\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{72}\right)\)
\(H=\dfrac{1}{90}+\left(\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}\right)\)
\(H=\dfrac{1}{90}+\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}\right)\)
\(H=\dfrac{1}{90}+\left(\dfrac{1}{2}-\dfrac{1}{8}\right)\)
\(H=\dfrac{1}{90}+\left(\dfrac{4}{8}-\dfrac{1}{8}\right)\)
\(H=\dfrac{1}{90}+\dfrac{3}{8}\)
\(H=\dfrac{49}{360}\)

\(\dfrac{9.3^2.1}{81.27}\)
\(=\dfrac{81.1}{81.27}\)
\(=\dfrac{3^4.1}{3^4.3^3}\)

Bạn tự vẽ hình nhé
a) Có IA + IB = AB (tính chất cộng đoạn thẳng)
=> IB = AB - IA = 8 - 4 = 4 cm
Mà IA = 4 cm
=> IA = IB (=4 cm)
kết hợp I nằm giữa AB
=> I là trung điểm của AB (đpcm)
b) Vì E là trung điểm của IA
=> IE = \(\dfrac{IA}{2}\) = \(\dfrac{4}{2}\) = 2 cm
Vì F là trung điểm của IB
=> IF = \(\dfrac{IB}{2}\) = \(\dfrac{4}{2}\) = 2 cm
Có EF = IF + IE (tính chất cộng đoạn thẳng)
=> EF = 2 + 2 = 4 cm

\(\dfrac{3x}{2.5}+\dfrac{3x}{5.8}+\dfrac{3x}{8.11}+\dfrac{3x}{11.14}=\dfrac{1}{21}\)
\(3x.\left(\dfrac{1}{2.5}+\dfrac{1}{5.8}+\dfrac{1}{8.11}+\dfrac{1}{11.14}\right)=\dfrac{1}{21}\)
\(3x\left(\dfrac{1}{2}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{14}\right)=\dfrac{1}{21}\)
\(3x.\left(\dfrac{1}{2}-\dfrac{1}{14}\right)\) \(=\dfrac{1}{21}\)
\(3x.\dfrac{3}{7}\) \(=\dfrac{1}{21}\)
\(3x\) \(=\dfrac{1}{21}:\dfrac{3}{7}\)
\(3x=\dfrac{1}{9}\)
\(x=\dfrac{1}{9}:3\)
\(x=\dfrac{1}{27}\)
1
x(3/2.5 + 3/5.8 + 3/8.11 + 3/11.14)=1/21
x(1/2 - 1/5 + 1/5 - 1/8 + 1/8 - 1/11 + 1/11- 1/14)=1/21
x(1/2 - 1/14)=1/21
x . 6/14=1/21
x=1/21 : 6/14=1/21 . 14/6=2/3

\(A=\dfrac{3.5.7.11.13.37-10101}{1212120+40404}\)
\(A=\dfrac{5.11.3.7.11.13-3.7.11.13}{120.10101+4.10101}\)
\(A=\dfrac{3.7.11.13.\left(5.11-1\right)}{10101\cdot\left(120+4\right)}\)
\(A=\dfrac{10101.54}{10101.124}\)
\(A=\dfrac{54}{124}=\dfrac{27}{62}\)
\(\Rightarrow\) Vậy \(A=\dfrac{27}{62}\)

Bài 2
a) 5/3 - x = 2 1/3
5/3 - x = 7/3
x = 5/3 - 7/3
x = -2/3
b) 3,5 - 1/2 x = -5/4
1/2 x = 3,5 - (-5/4)
1/2 x = 19/4
x = 19/4 : 1/2
x = 19/2
c) 4/(2 - x) - 2/3 = 0
4/(2 - x) = 2/3
2(2 - x) = 3.4
2(2 - x) = 12
2 - x = 12 : 2
2 - x = 6
x = 2 - 6
x = -4
d) 0,25 + 7,5% x = 2 5/6
3/40 x = 17/6 - 0,25
3/40 x = 31/12
x = 31/12 : 3/40
x = 310/9
Bài 4
a) Số học sinh xếp loại tốt:
120 . 4/15 = 32 (học sinh)
Số học sinh xếp loại khá:
32 : 80% = 40 (học sinh)
Số học sinh xếp loại đạt:
120 - 32 - 40 = 48 (học sinh)
b) Tỉ số phần trăm của số học sinh xếp loại khá so với cả khối:
40 . 100% : 120 ≈ 33,33%

Bài 5:
1: \(\dfrac{2}{5}+\dfrac{3}{5}x=\dfrac{9}{20}\)
=>\(\dfrac{3}{5}x=\dfrac{9}{20}-\dfrac{2}{5}=\dfrac{9}{20}-\dfrac{8}{10}=\dfrac{1}{10}\)
=>\(x=\dfrac{1}{10}:\dfrac{3}{5}=\dfrac{1}{10}\cdot\dfrac{5}{3}=\dfrac{5}{30}=\dfrac{1}{6}\)
2: \(\dfrac{1}{4}+\dfrac{1}{3}:\left(3x\right)=-5\)
=>\(\dfrac{1}{3}:\left(3x\right)=-5-\dfrac{1}{4}=-\dfrac{21}{4}\)
=>\(3x=-\dfrac{1}{3}:\dfrac{21}{4}=-\dfrac{1}{3}\cdot\dfrac{4}{21}=-\dfrac{4}{63}\)
=>\(x=-\dfrac{4}{63}:3=-\dfrac{4}{189}\)
3: \(-\dfrac{21}{13}x+\dfrac{1}{3}=-\dfrac{2}{3}\)
=>\(-\dfrac{21}{13}x=-\dfrac{2}{3}-\dfrac{1}{3}=-\dfrac{3}{3}=-1\)
=>\(x=1:\dfrac{21}{13}=\dfrac{13}{21}\)
4: \(\dfrac{3}{4}x-\dfrac{1}{2}=\dfrac{3}{7}\)
=>\(\dfrac{3}{4}x=\dfrac{1}{2}+\dfrac{3}{7}=\dfrac{7+6}{14}=\dfrac{13}{14}\)
=>\(x=\dfrac{13}{14}:\dfrac{3}{4}=\dfrac{13}{14}\cdot\dfrac{4}{3}=\dfrac{52}{42}=\dfrac{26}{21}\)
5: \(\dfrac{2}{3}x+\dfrac{1}{2}=\dfrac{3}{10}-\dfrac{1}{5}\)
=>\(\dfrac{2}{3}x+\dfrac{1}{2}=\dfrac{1}{10}\)
=>\(\dfrac{2}{3}x=\dfrac{1}{10}-\dfrac{1}{2}=\dfrac{1}{10}-\dfrac{5}{10}=-\dfrac{4}{10}=-\dfrac{2}{5}\)
=>\(x=-\dfrac{2}{5}:\dfrac{2}{3}=-\dfrac{2}{5}\cdot\dfrac{3}{2}=-\dfrac{3}{5}\)
6: \(\dfrac{2}{3}+\dfrac{1}{3}x=-\dfrac{1}{2}\)
=>\(\dfrac{1}{3}x=-\dfrac{1}{2}-\dfrac{2}{3}=\dfrac{-7}{6}\)
=>\(x=-\dfrac{7}{6}:\dfrac{1}{3}=-\dfrac{7}{6}\cdot3=-\dfrac{7}{2}\)
7: \(\dfrac{11}{12}x+\dfrac{3}{4}=-\dfrac{1}{6}\)
=>\(\dfrac{11}{12}x=-\dfrac{1}{6}-\dfrac{3}{4}=\dfrac{-2}{12}-\dfrac{9}{12}=-\dfrac{11}{12}\)
=>x=-1
8: \(-\dfrac{5}{6}-\dfrac{2}{3}x=\dfrac{7}{12}+\dfrac{-1}{3}\)
=>\(-\dfrac{5}{6}-\dfrac{2}{3}x=\dfrac{7}{12}-\dfrac{4}{12}=\dfrac{3}{12}=\dfrac{1}{4}\)
=>\(\dfrac{2}{3}x=-\dfrac{5}{6}-\dfrac{1}{4}=\dfrac{-10}{12}-\dfrac{3}{12}=-\dfrac{13}{12}\)
=>\(x=-\dfrac{13}{12}:\dfrac{2}{3}=-\dfrac{13}{12}\cdot\dfrac{3}{2}=\dfrac{-39}{24}=\dfrac{-13}{8}\)
9: \(2\dfrac{2}{3}x+8\dfrac{2}{3}=3\dfrac{1}{3}\)
=>\(\dfrac{8}{3}x=3+\dfrac{1}{3}-8-\dfrac{2}{3}=-5-\dfrac{1}{3}=-\dfrac{16}{3}\)
=>\(x=-\dfrac{16}{3}:\dfrac{8}{3}=-\dfrac{16}{3}\cdot\dfrac{3}{8}=-\dfrac{16}{8}=-2\)
10: \(\dfrac{3}{4}-\dfrac{1}{4}:\left(x:\dfrac{5}{2}\right)=-3\)
=>\(\dfrac{1}{4}:\left(x:\dfrac{5}{2}\right)=\dfrac{3}{4}+3=\dfrac{15}{4}\)
=>\(x:\dfrac{5}{2}=\dfrac{1}{4}:\dfrac{15}{4}=\dfrac{1}{15}\)
=>\(x=\dfrac{1}{15}\cdot\dfrac{5}{2}=\dfrac{1}{6}\)

1: Khối lượng của quả dưa là:
\(\dfrac{7}{2}:\dfrac{3}{4}=\dfrac{7}{2}\cdot\dfrac{4}{3}=\dfrac{14}{3}\left(kg\right)\)
Câu 2:
a: Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOy}< \widehat{xOz}\)
nên tia Oy nằm giữa hai tia Ox và Oz
=>\(\widehat{xOy}+\widehat{yOz}=\widehat{xOz}\)
=>\(\widehat{yOz}+40^0=120^0\)
=>\(\widehat{yOz}=80^0\)
b: Ta có: \(\widehat{xOy}+\widehat{xOt}=180^0\)(hai góc kề bù)
=>\(\widehat{xOt}+40^0=180^0\)
=>\(\widehat{xOt}=140^0\)
c: Om là phân giác của góc yOz
=>\(\widehat{yOm}=\widehat{zOm}=\dfrac{\widehat{yOz}}{2}=\dfrac{80^0}{2}=40^0\)
Vì \(\widehat{zOm}< \widehat{zOx}\)
nên tia Om nằm giữa hai tia Oz và Ox
=>\(\widehat{mOz}+\widehat{mOx}=\widehat{xOz}=120^0\)
=>\(\widehat{xOm}=120^0-40^0=80^0\)
Vì \(\widehat{xOy}+\widehat{yOm}=40^0+40^0=80^0=\widehat{xOm}\)
và \(\widehat{xOy}=\widehat{yOm}\left(=40^0\right)\)
nên Oy là phân giác của góc xOm
bạn trl 1 câu cũng được nhé làm được câu nào trl câu .mik cũng sẽ tick cho các bạn nếu bạn nào giúp mình trl lời mà trl câu nào cũng được

\(A=\dfrac{2024}{1.2}+\dfrac{2024}{2.3}+\dfrac{2024}{3.4}+...+\dfrac{2024}{2023.2024}\)
\(A=2024.\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{2023.2024}\right)\)
\(A=2024.\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2023}-\dfrac{1}{2024}\right)\)
\(A=2024.\left(1-\dfrac{1}{2024}\right)\)
\(A=2024.\dfrac{2023}{2024}\)
\(A=\dfrac{2024}{1}.\dfrac{2023}{2024}\)
\(A=1.2023\)
\(A=2023\)
\(\Rightarrow\) Vậy \(A=2023\)
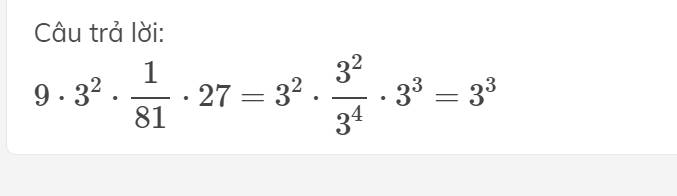


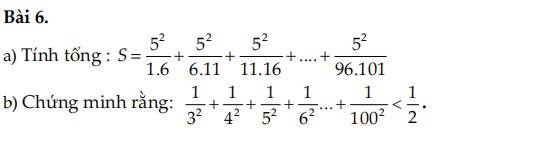

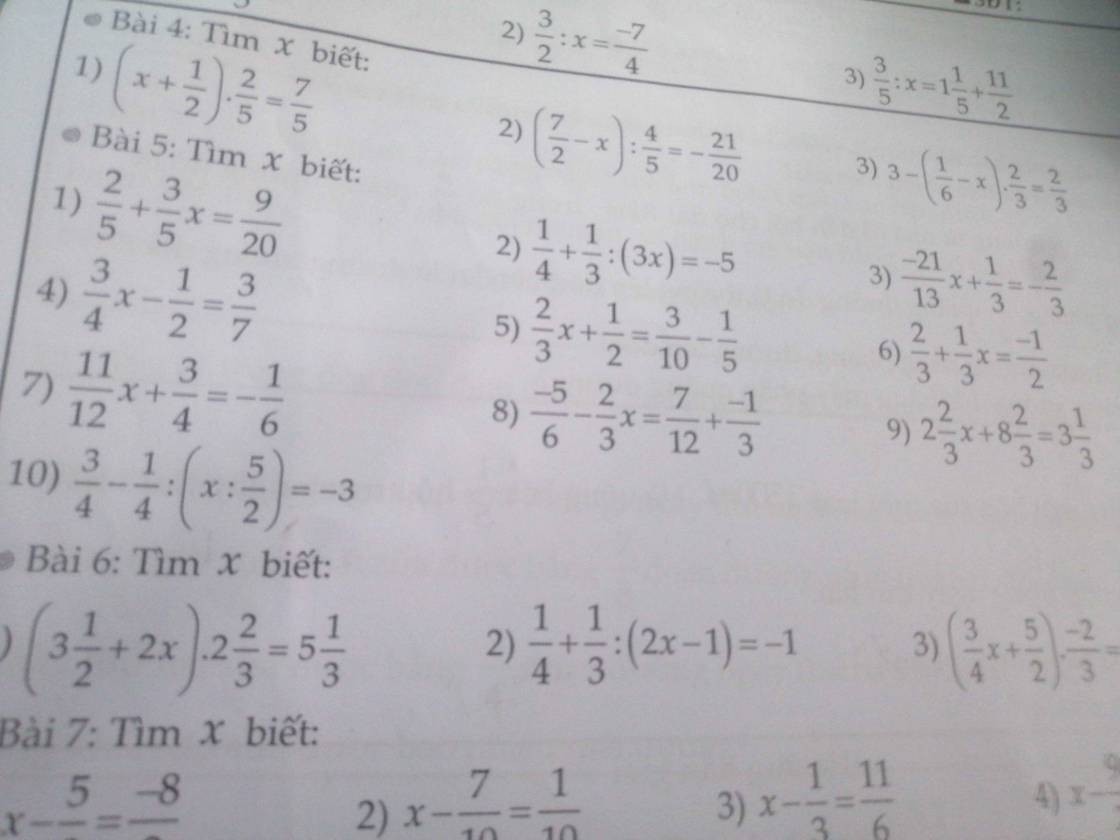
\(9\cdot3^2\cdot\dfrac{1}{81}\cdot27=3^2\cdot\dfrac{3^2}{3^4}\cdot3^3=3^3\)