Giúp mình bài này với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(\dfrac{12}{5}>\dfrac{10}{5}=2=\dfrac{4}{2}>\dfrac{3}{2}\) (Số 2 làm trung gian)
Hay \(\dfrac{12}{5}>\dfrac{3}{2}\)
b) Ta có:
`2023 < 2024 =>` \(\dfrac{2023}{2024}< 1\)
`2026 > 2025 =>` \(\dfrac{2026}{2025}>1\)
=> \(\dfrac{2023}{2024}< 1< \dfrac{2026}{2025}\) (1 làm trung gian)
Hay \(\dfrac{2023}{2024}< \dfrac{2026}{2025}\)
a: \(\dfrac{12}{5}=2,4;\dfrac{3}{2}=1,5\)
mà 2,4>1,5
nên \(\dfrac{12}{5}>\dfrac{3}{2}\)
b: \(\dfrac{2023}{2024}< \dfrac{2024}{2024}=1;\dfrac{2026}{2025}>\dfrac{2025}{2025}=1\)
Do đó: \(\dfrac{2023}{2024}< \dfrac{2026}{2025}\)

Bài 4:
a: 4x-y=1
=>y=4x-1
Vậy: Nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=4x-1\end{matrix}\right.\)
b: x+3y=-2
=>x=-3y-2
Vậy: Nghiệm tổng quát là \(\left\{{}\begin{matrix}y\in R\\x=-3y-2\end{matrix}\right.\)
Bài 5:
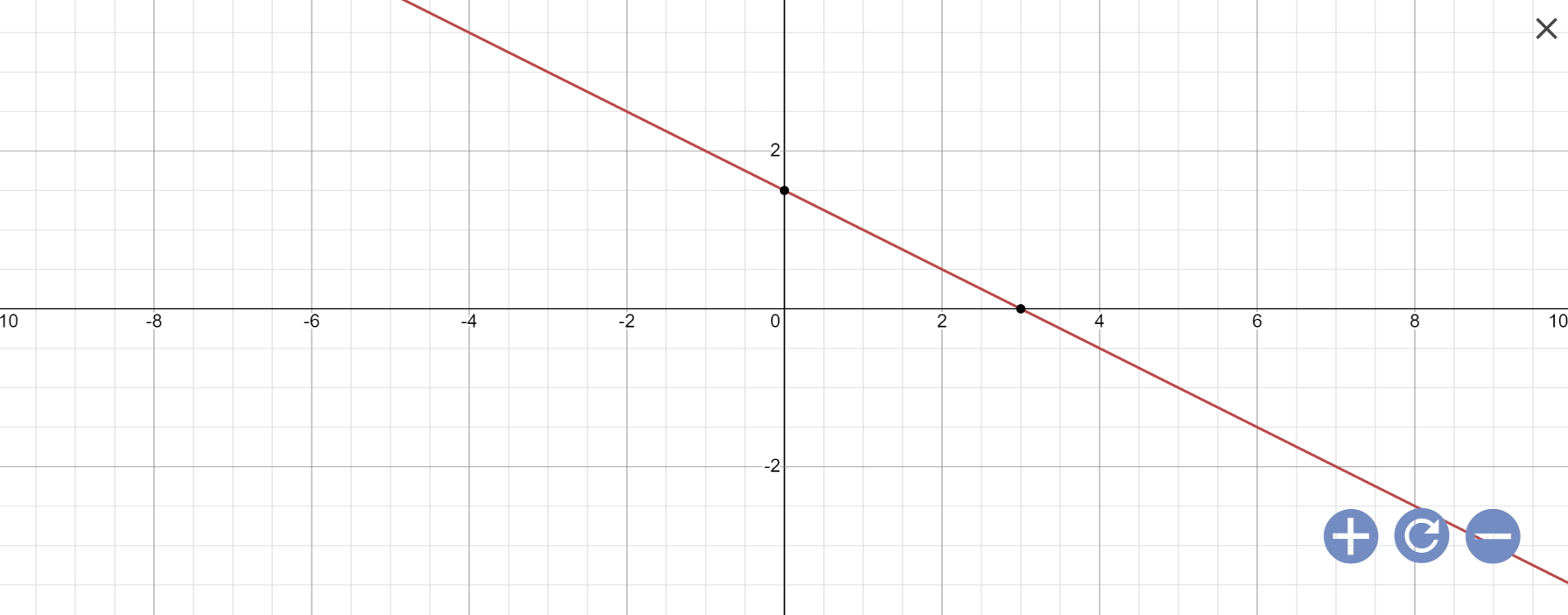
x+2y-3=0
=>2y=-x+3
=>\(y=\dfrac{-x+3}{2}\)
Vậy: Nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=\dfrac{-x+3}{2}\end{matrix}\right.\)
Biểu diễn tập nghiệm:

a: 2<3
=>\(2+8,5\cdot6< 3+8,5\cdot6\)
b: 2<3
=>\(\sqrt{2}< \sqrt{3}\)
=>\(-\sqrt{2}>-\sqrt{3}\)
=>\(30-\sqrt{2}>30-\sqrt{3}\)
c:
Vì 3>2
nên \(3\sqrt{3}>3\sqrt{2}\)
=>\(-3\sqrt{3}< -3\sqrt{2}\)
mà 35<36
nên \(35-3\sqrt{3}< 36-3\sqrt{2}\)

a: 2a+3>2b+3
=>2a>2b
=>a>b
b: -3a-1>=-3b-1
=>\(-3a>=-3b\)
=>3a<=3b
=>a<=b
c: 5-2a<5-a-b
=>5-2a+a<5-b
=>5-a<5-b
=>a-5>b-5
=>a>b

a: \(x^2+y^2>=2xy\)
=>\(x^2-2xy+y^2>=0\)
=>\(\left(x-y\right)^2>=0\)(luôn đúng)
b: \(x^2+4xy>=-4y^2\)
=>\(x^2+4xy+4y^2>=0\)
=>\(\left(x+2y\right)^2>=0\)(luôn đúng)
c: \(2\left(x^2+y^2\right)>=\left(x+y\right)^2\)
=>\(2x^2+2y^2-x^2-2xy-y^2>=0\)
=>\(x^2-2xy+y^2>=0\)
=>\(\left(x-y\right)^2>=0\)(luôn đúng)

a: \(\dfrac{x}{y}+\dfrac{y}{x}>=2\cdot\sqrt{\dfrac{x}{y}\cdot\dfrac{y}{x}}=2\)
b: \(\dfrac{1}{x}+\dfrac{1}{y}>=\dfrac{4}{x+y}\)
=>\(\dfrac{x+y}{xy}>=\dfrac{4}{x+y}\)
=>\(\left(x+y\right)^2>=4xy\)
=>\(x^2+2xy+y^2-4xy>=0\)
=>\(x^2-2xy+y^2>=0\)
=>\(\left(x-y\right)^2>=0\)(luôn đúng)

a: \(\left\{{}\begin{matrix}2\left(x+y\right)+3\left(x-y\right)=4\\x+y+2\left(x-y\right)=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+2y+3x-3y=4\\x+y+2x-2y=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5x-y=4\\3x-y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x-y-3x+y=4-5\\3x-y=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x=-1\\y=3x-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=3\cdot\dfrac{-1}{2}-5=-\dfrac{3}{2}-5=-\dfrac{13}{2}\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}\left(x+1\right)\left(y-1\right)=xy-1\\\left(x-3\right)\left(y+3\right)=xy-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}xy-x+y-1=xy-1\\xy+3x-3y-9=xy-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-x+y=0\\3x-3y=6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x-y=0\\x-y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-y-x+y=0-2\\x-y=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}0y=-2\\x-y=0\end{matrix}\right.\Leftrightarrow\left(x;y\right)\in\varnothing\)

\(1.2\left(x+2\right)^2< 2x\left(x+2\right)+4\\ \Leftrightarrow2\left(x^2+4x+4\right)-2x\left(x+2\right)-4< 0\\ \Leftrightarrow2x^2+8x+4-2x^2-4x-4< 0\\ \Leftrightarrow4x< 0\\ \Leftrightarrow x< 0\\ 2.\left(x-1\right)^2+x^2< \left(x+1\right)^2+\left(x+2\right)^2\\ \Leftrightarrow x^2-2x+1+x^2< x^2+2x+1+x^2+4x+4\\ \Leftrightarrow2x^2-2x+1-2x^2-6x-5< 0\\ \Leftrightarrow-8x-4< 0\\ \Leftrightarrow8x>-4\\ \Leftrightarrow x>-\dfrac{1}{2}\\ 3.\left(x^2+1\right)\left(x-6\right)< \left(x-2\right)^3\\ \Leftrightarrow x^3-6x^2+x-6< x^3-6x^2+12x-8\\ \Leftrightarrow x-6< 12x-8\\ \Leftrightarrow12x-x>-6+8\\ \Leftrightarrow11x>2\\ \Leftrightarrow x>\dfrac{2}{11}\)

Diện tích tam giác BAC là:
\(S_{BAC}=\dfrac{1}{2}\cdot BA\cdot BC\cdot sinABC=\dfrac{1}{2}\cdot5,2\cdot3,5\cdot sin75=\dfrac{91\sqrt{6}+91\sqrt{2}}{40}\)
ABCD là hình bình hành
=>\(S_{ABCD}=2\cdot S_{BAC}=\dfrac{91\sqrt{6}+91\sqrt{2}}{20}\)

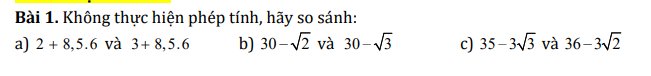
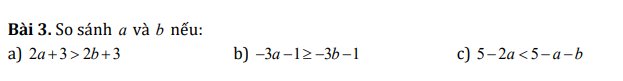


a: Ta có: \(AE=EB=\dfrac{AB}{2}\)
\(BF=FC=\dfrac{BC}{2}\)
\(DK=KC=\dfrac{DC}{2}\)
mà AB=BC=CD
nên AE=EB=BF=FC=DK=KC
Xét tứ giác AECK có
AE//CK
AE=CK
Do đó: AECK là hình bình hành
b: Xét ΔDCF vuông tại C và ΔCBE vuông tại B có
DC=CB
CF=BE
Do đó: ΔDCF=ΔCBE
=>\(\widehat{DFC}=\widehat{CEB}\)
mà \(\widehat{CEB}+\widehat{BCE}=90^0\)
nên \(\widehat{BCE}+\widehat{DFC}=90^0\)
=>CE\(\perp\)DF