Bài 3: Một chiếc đồng hồ mỗi giờ nhanh 3 phút. Sáng nay, lúc ti vi báo năm giờ người ta chỉnh lại đồng hồ. Hỏi đến 8 giờ tối hôm nay thì đồng hồ đó chỉ mấy giờ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a.
$=\frac{10-8xy^3+12xy^3+10}{4x^3y^2}=\frac{20+4xy^3}{4x^3y^2}$
$=\frac{5+xy^3}{x^3y^2}$
b.
$=\frac{4(x-2)+2(x+2)}{(x+2)(x-2)}+\frac{6-5x}{(x-2)(x+2)}$
$=\frac{6x-4}{(x+2)(x-2)}+\frac{6-5x}{(x-2)(x+2)}$
$=\frac{x+2}{(x-2)(x+2)}=\frac{1}{x-2}$
c.
$=\frac{4x+7-(3x+6)}{2x+2}=\frac{x+1}{2(x+1)}=\frac{1}{2}$
d.
$=\frac{y+6}{(y-2)(y+2)}-\frac{2}{y(y+2)}$
$=\frac{y(y+6)-2(y-2)}{y(y+2)(y-2)}=\frac{y^2+4y+4}{y(y+2)(y-2)}=\frac{(y+2)^2}{y(y+2)(y-2)}=\frac{y+2}{y(y-2)}$
e.
$=\frac{4y+7}{3y+2}.\frac{3y+2}{8y+14}=\frac{4y+7}{8y+14}=\frac{4y+7}{2(4y+7)}=\frac{1}{2}$
g.
$=\frac{3y+2}{4(2y+3)}.\frac{2y+3}{3y+2}=\frac{1}{4}$
h.
$=\frac{2y+3}{y+3}.\frac{3(y+3)}{2y+3}=3$


Lời giải:
a. $=\frac{6xy^2.3y}{6xy^2.4x^2}=\frac{3y}{4x^2}$
b.
$=\frac{(x-y)(x^2+xy+y^2)}{(x-y)(x+y)}=\frac{x^2+xy+y^2}{x+y}$
c.
$=\frac{5(4x^2-9)}{(2x+3)^2}=\frac{5(2x-3)(2x+3)}{(2x+3)^2}=\frac{5(2x-3)}{2x+3}$
d.
$=\frac{4x(x^2+2x+1)}{2x^2(x+1)}=\frac{4x(x+1)^2}{2x^2(x+1)}=\frac{2(x+1)}{x}$

Lời giải:
a. Bạn tự vẽ hình
b. PT hoành độ giao điểm của $(d), (d')$:
$x+2=-2x+8\Leftrightaarrow 3x=6\Leftrightarrow x=2$
$y=x+2=2+2=4$
Vậy $A$ có tọa độ $(2,4)$
$B\in Ox$ nên $y_B=0$
$B\in (d)$ nên $y_B=x_B+2\Rightarrow x_B=y_B-2=0-2=-2$
Vậy $B(-2,0)$
$C\in Ox$ nên $y_C=0$
$C\in (d')$ nên $y_C=-2x_C+8\Rightarrow x_C=\frac{y_C-8}{-2}=\frac{-8}{-2}=4$
Vậy $C(4,0)$
Diện tích tam giác $ABC$:
$S_{ABC}=\frac{d(A,BC).BC}{2}=\frac{d(A,Ox).BC}{2}=\frac{|y_A|(|x_B|+|x_C|)}{2}=\frac{4(2+4)}{2}=12$ (đvdt)

Sự vật là một phần trong danh từ
Con người là chủ nhân của thế giới
Đồ vật là những đồ dùng không thể thiếu trong cuộc sống
Con vật là người bạn đồng hành gần gũi thân thiết nhất của con người

a.
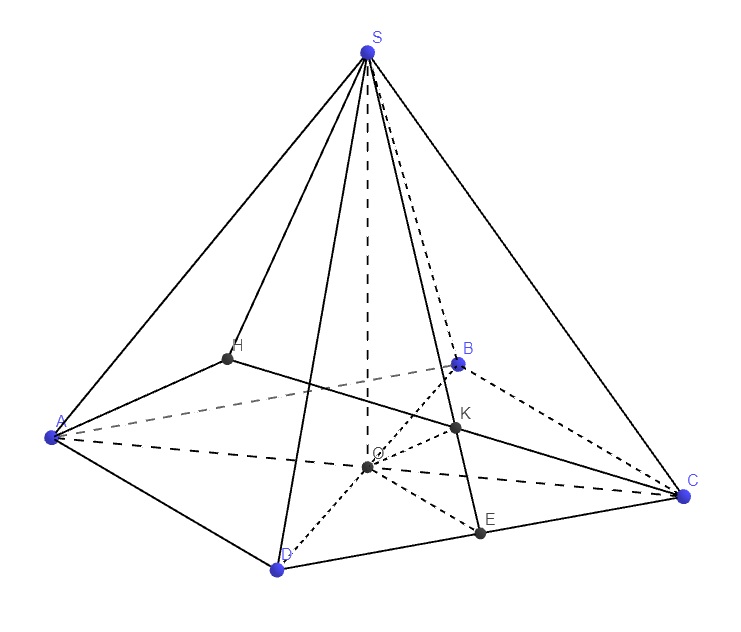
Do chóp S.ABCD đều \(\Rightarrow SO\perp\left(ABCD\right)\)
\(\Rightarrow\) O là hình chiếu vuông góc của S lên (ABCD)
\(\Rightarrow\Delta OAB\) là hình chiếu vuông góc của \(\Delta SAB\) lên (ABCD)
b.
Gọi E là trung điểm CD \(\Rightarrow OE\) là đường trung bình tam giác BCD
\(\Rightarrow OE||BC\Rightarrow OE\perp CD\)
\(\Rightarrow CD\perp\left(SOE\right)\)
Trong mp (SOE), từ O kẻ \(OK\perp SE\)
\(OK\in\left(SOE\right)\Rightarrow CD\perp OK\)
\(\Rightarrow OK\perp\left(SCD\right)\)
Trong mp (ACK), qua A kẻ đường thẳng song song OK cắt CK kéo dài tại H
\(\Rightarrow AH\perp\left(SCD\right)\Rightarrow SH\) là hình chiếu vuông góc của SA lên (SCD)
\(\Rightarrow\widehat{ASH}\) là góc giữa SA và (SCD) hay \(\widehat{ASH}=\varphi\)
\(OE=\dfrac{1}{2}BC=\dfrac{a}{2}\)
Áp dụng hệ thức lượng trong tam giác vuông SOE:
\(OK=\dfrac{SO.OE}{\sqrt{SO^2+OE^2}}=\dfrac{a\sqrt{5}}{5}\)
O là trung điểm AC và \(OK||SH\Rightarrow OK\) là đường trung bình tam giác CAH
\(\Rightarrow AH=2OK=\dfrac{2a\sqrt{5}}{5}\)
\(OA=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\Rightarrow SA=\sqrt{SO^2+OA^2}=\dfrac{a\sqrt{6}}{2}\)
\(\Rightarrow sin\varphi=\dfrac{AH}{SA}=\dfrac{2\sqrt{30}}{15}\)
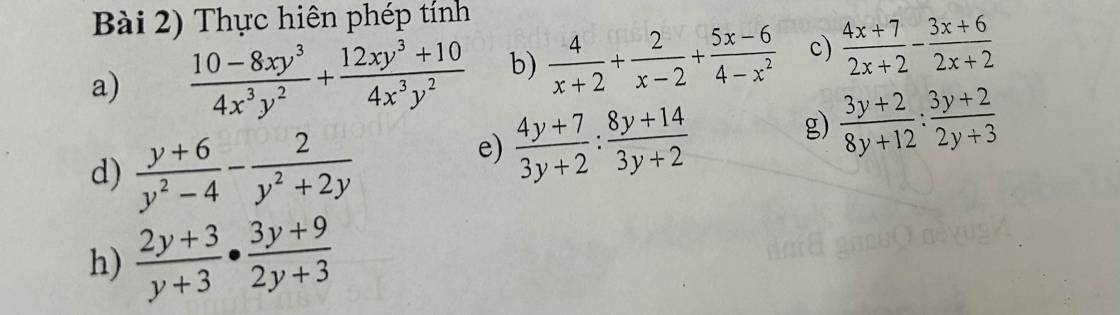
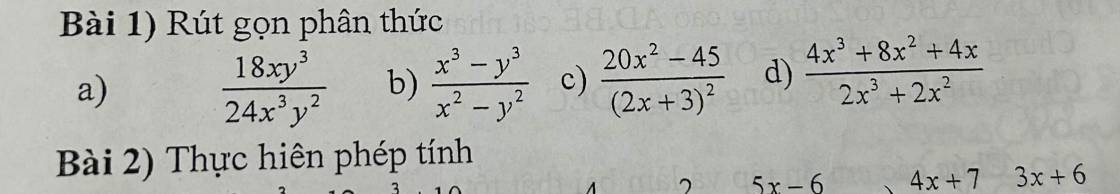


8 giờ tối = 20 giờ
Từ 5 giờ sáng đến 8 giờ tối có:
20 giờ - 5 giờ = 15 (giờ)
Mỗi giờ sớm 3 phút nên lúc 8 giờ tối đồng hồ chỉ:
8 giờ + 3 × 15 phút = 8 giờ 45 phút