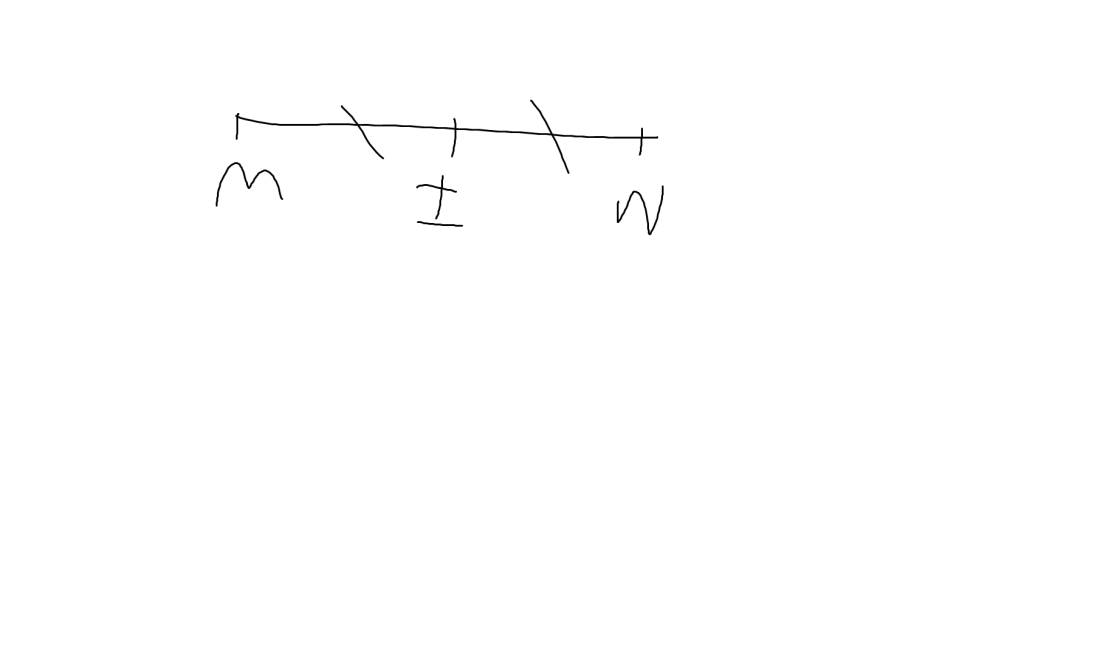
a: Vì OA và OB là hai tia đối nhau

nên O nằm giữa A và B

Ta có: O nằm giữa A và B

OA=OB(=3cm)

Do đó: O là trung điểm của AB

b: Trên tia Oy, ta có: OC<OB

nên C nằm giữa O và B

Để C là trung điểm của OB nên \(OC=\dfrac{OB}{2}\)

=>\(a=\dfrac{3}{2}=1,5\left(cm\right)\)

\(\dfrac{-3}{8}\cdot16\cdot\dfrac{8}{17}-0,375\cdot7\cdot\dfrac{9}{17}\)

\(=-\dfrac{3}{8}\cdot\dfrac{128}{17}-\dfrac{3}{8}\cdot\dfrac{63}{17}\)

\(=-\dfrac{3}{8}\left(\dfrac{128}{17}+\dfrac{63}{17}\right)=-\dfrac{3}{8}\cdot\dfrac{191}{17}=\dfrac{-573}{136}\)

- \(\dfrac{3}{8}\).16.\(\dfrac{8}{17}\) - 0,375.7\(\dfrac{9}{17}\)

Đề như này phải không em?

Gọi d=ƯCLN(-6n+5;4n-3)

=>\(\left\{{}\begin{matrix}-6n+5⋮d\\4n-3⋮d\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}12n-10⋮d\\12n-9⋮d\end{matrix}\right.\)

=>\(12n-10-12n+9⋮d\)

=>\(-1⋮d\)

=>d=1

=>ƯCLN(-6n+5;4n-3)=1

=>\(\dfrac{-6n+5}{4n-3}\) là phân số tối giản

Bài 8:

\(\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{97\cdot99}\)

\(=\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{97}-\dfrac{1}{99}\)

\(=\dfrac{1}{3}-\dfrac{1}{99}=\dfrac{33}{99}-\dfrac{1}{99}=\dfrac{32}{99}\)

Bài 6:

a: 

b: I là trung điểm của MN

=>\(MI=\dfrac{MN}{2}=\dfrac{7}{2}=3,5\left(cm\right)\)

giải theo kiểu lớp 6 được ko ạ?

Căn bậc hai là của lớp 7 ak.

\(x^2-2=0\)

=>\(x^2=2\)

=>\(x=\pm\sqrt{2}\)

a: SỐ tiền lãi anh Duy nhận được sau 1 năm là:

\(200\cdot10^6\cdot5,6\%=11200000\left(đồng\right)\)

Số tiền cả gốc lẫn lãi anh Duy nhận được là:

\(200000000+11200000=211200000\left(đồng\right)\)

b: Số tiền lãi năm thứ hai anh Duy nhận được là:

\(211200000\cdot8\%=16896000\left(đồng\right)\)

Tổng số tiền anh Duy nhận được là:

\(211200000+16896000=228096000\left(đồng\right)\)

Ta có:

\(2020+2021+2022< 2021+2022+2023\)

\(\Rightarrow\dfrac{2020+2021+2022}{2021+2022+2023}< 1\)

\(\Rightarrow Q< 1\)

Lại có: \(2020.2>2021.1\Rightarrow\dfrac{2020}{2021}>\dfrac{1}{2}\)

\(2021.2>2022.1\Rightarrow\dfrac{2021}{2022}>\dfrac{1}{2}\)

\(2022.2>2023.1\Rightarrow\dfrac{2022}{2023}>\dfrac{1}{2}\)

\(\Rightarrow\dfrac{2020}{2021}+\dfrac{2021}{2022}+\dfrac{2022}{2023}>\dfrac{1}{2}+\dfrac{1}{2}+\dfrac{1}{2}=\dfrac{3}{2}\)

\(\Rightarrow P>\dfrac{3}{2}>1\)

\(\Rightarrow P>Q\)

^{\(\dfrac{2020}{2021}\) > \(\dfrac{2020}{2021+2022+2023}\)}

^{\(\dfrac{2021}{2022}\) > \(\dfrac{2021}{2021+2022+2023}\)}

^{\(\dfrac{2022}{2023}\) > \(\dfrac{2022}{2021+2022+2023}\)}

^{Cộng vế với vế ta có: P = \(\dfrac{2020}{2021}\) + \(\dfrac{2021}{2022}\) + \(\dfrac{2022}{2023}\) > \(\dfrac{2020+2021+2022}{2021+2022+2023}\) = Q}

Ta có: \(6xy+4x+15y+18=0\\ \Leftrightarrow\left(6xy+15y\right)+\left(4x+18\right)=0\\ \Leftrightarrow3y\left(2x+5\right)+2\left(2x+6\right)=0\Leftrightarrow3y\left(2x+5\right)+2\left(2x+5\right)+2=0\\ \Leftrightarrow\left(2x+5\right)\left(3y+2\right)=-2\)

Vì \(x,y\inℤ\) nên \(2x+5\inℤ;3y+2\inℤ\) 

\(\Rightarrow\left(2x+5;3y+2\right)\inƯ\left(-2\right)\\\Rightarrow\left(2x+5;3y+2\right)\in \left\{\pm1;\pm2\right\}\)

Ta có bảng sau:

\(\Rightarrow\left(x;y\right)\in\left\{\left(\dfrac{8}{11};-\dfrac{1}{11}\right);\left(\dfrac{1}{11};\dfrac{4}{11}\right);\left(-\dfrac{8}{11};\dfrac{1}{11}\right);\left(-\dfrac{1}{11};-\dfrac{4}{11}\right)\right\}\)(Loại)

Vậy không có nghiệm \(x,y\inℤ\)

\(-\dfrac{2}{7}+\dfrac{5}{12}\cdot\dfrac{18}{35}\)

\(=\dfrac{-2}{7}+\dfrac{18}{12}\cdot\dfrac{5}{35}\)

\(=-\dfrac{2}{7}+\dfrac{3}{2}\cdot\dfrac{1}{7}=\dfrac{-2}{7}+\dfrac{3}{14}=\dfrac{-4+3}{14}=-\dfrac{1}{14}\)

-2/7 + 5/12 . 18/35

= -2/7 + 1/2 . 3/7

= -2/7 + 3/14

= -4/14 + 3/14

= 1/14

\(\dfrac{x}{3}-\dfrac{2}{y}=\dfrac{1}{5}\)

=>\(\dfrac{xy-6}{3y}=\dfrac{1}{5}\)

=>5(xy-6)=3y

=>5xy-30=3y

=>5xy-3y=30

=>y(5x-3)=30

mà 5x-3>=-3 và y>=0(vì x và y là số tự nhiên)

nên \(\left(5x-3\right)\cdot y=30\cdot1=15\cdot2=10\cdot3=6\cdot5=5\cdot6=3\cdot10=2\cdot15=1\cdot30\)

=>\(\left(x;y\right)\in\left\{\left(\dfrac{33}{5};1\right);\left(\dfrac{18}{5};2\right);\left(\dfrac{13}{5};3\right);\left(\dfrac{9}{5};5\right);\left(\dfrac{8}{5};6\right);\left(\dfrac{6}{5};10\right);\left(1;15\right);\left(\dfrac{4}{5};30\right)\right\}\)

mà x,y là các số tự nhiên

nên \(\left(x;y\right)\in\left(1;15\right)\)