lớp 7a có 4 bạn làm vệ sinh lớp hết 2 giờ. nếu có 16 bạn (năng xuất làm việc như nha) thì làm trong bao lâu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{-3}{4}\) = \(\dfrac{-9}{12}\)
\(\dfrac{-3}{-9}\) = \(\dfrac{4}{12}\); \(\dfrac{-9}{-3}\) = \(\dfrac{12}{4}\); \(\dfrac{4}{-3}\) = \(\dfrac{12}{-9}\)

\(\dfrac{5^{2023}\cdot3^4+5^{2023}\cdot19}{5^{2025}}\)
\(=\dfrac{5^{2023}\left(3^4+19\right)}{5^{2025}}\)
\(=\dfrac{5^{2023}\cdot100}{5^{2023}\cdot25}=\dfrac{100}{25}=4\)

\(\left(\dfrac{3}{4}-81\right)\left(\dfrac{3^2}{5}-81\right)\left(\dfrac{3^3}{6}-81\right)\cdot...\cdot\left(\dfrac{3^{2000}}{2003}-81\right)\)
\(=\left(\dfrac{3^6}{9}-81\right)\left(\dfrac{3}{4}-81\right)\cdot...\cdot\left(\dfrac{3^{2000}}{2003}-81\right)\)
\(=\left(81-81\right)\left(\dfrac{3}{4}-81\right)\cdot...\cdot\left(\dfrac{3^{2000}}{2003}-81\right)\)
=0


Lời giải:
Vì $|\frac{1}{3}+2019x|+|\frac{2}{3}+2020x|\geq 0$ với mọi $x\in\mathbb{R}$
$\Rightarrow 4040x\geq 0\Rightarrow x\geq 0$
$\Rightarrow |\frac{1}{3}+2019x|=\frac{1}{3}+2019x; |\frac{2}{3}+2020x|=\frac{2}{3}+2020x$
Bài toán trở thành:
$\frac{1}{3}+2019x+\frac{2}{3}+2020x=4040x$
$\Rightarrow 1+4039x=4040x$
$\Rightarrow x=1$ (tm)

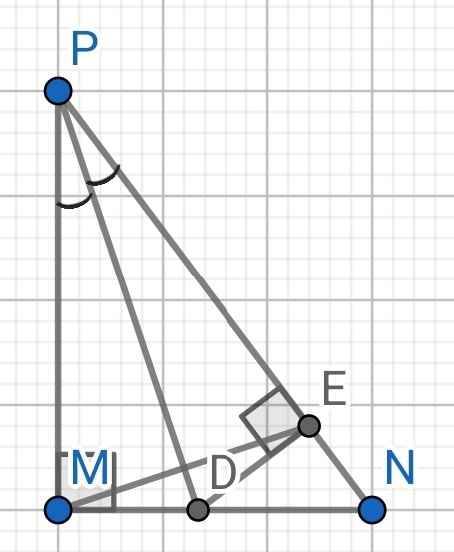
a) Sửa đề: Chứng minh ∆PMD = ∆PED
Do PD là tia phân giác của ∠MPN (gt)
⇒ ∠MPD = ∠EPD
Xét hai tam giác vuông: ∆PMD và ∆PED có:
PD là cạnh chung
∠MPD = ∠EPD (cmt)
⇒ ∆PMD = ∆PED (cạnh huyền - góc nhọn)
b) Do ∆PMD = ∆PED (cmt)
⇒ PM = PE (hai cạnh tương ứng)
⇒ ∆PEM cân tại P
⇒ ∠PEM = ∠PME
c) Do ∆PMD = ∆PED (cmt)
⇒ DM = DE (hai cạnh tương ứng)
∆DEN vuông tại E (do DE ⊥ PN)
⇒ DN là cạnh huyền nên là cạnh lớn nhất
⇒ DN > DE
Mà DE = DM (cmt)
⇒ DN > DM

Bài 5:
Thay x=1 và y=-2 vào Q, ta được:
\(Q=1^2\cdot\left(-2\right)-3\cdot1\cdot\left(-2\right)+2\cdot1\cdot\left(-2\right)^2-1\)
=-2+6+8-1
=4+8-1
=11
bài 4:
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
=>BA=BE
b: Ta có: ΔBAD=ΔBED
=>DA=DE
mà DE<DC(ΔDEC vuông tại E)
nên DA<DC
c: Ta có: ΔBHA vuông tại H
=>BH<BA
mà BA=BE(cmt)
nên BH<BE
mà BE<BC(E nằm giữa B và C)
nên BH<BE<BC

Bài 5:
Thay x=1 và y=-2 vào Q, ta được:
\(Q=1^2\cdot\left(-2\right)-3\cdot1\cdot\left(-2\right)+2\cdot1\cdot\left(-2\right)^2-1\)
=-2+6+8-1
=4+8-1
=11
bài 4:
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
=>BA=BE
b: Ta có: ΔBAD=ΔBED
=>DA=DE
mà DE<DC(ΔDEC vuông tại E)
nên DA<DC
c: Ta có: ΔBHA vuông tại H
=>BH<BA
mà BA=BE(cmt)
nên BH<BE
mà BE<BC(E nằm giữa B và C)
nên BH<BE<BC
Nếu có 16 bạn thì công việc sẽ hoàn thành trong:
4*2:16=0,5(giờ)
16 bạn làm xong trong: 2 x 4: 16 = 0,5 giờ = 30 phút