Phân tích mỗi đa thức sau thành nhân tử
a)x^3-2x^2y+xy^2+xy
b)x^3+4x^2y+4xy^2-9x
c)x^3-y^3+x-y
d)4x^2-4xy+2x-y+y^2
e)9x^2-3x+2y-4y^2
f)3x^2-6xy+3y^2-5x+5y
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn cần bài nào thì nên ghi chú rõ bài đó ra. Nếu cần nhiều bài thì nên tách lẻ mỗi bài một post để được hỗ trợ tốt hơn.

Lời giải:
$x^4+ax^2+b=x^2(x^2-x+1)+x(x^2-x+1)+ax^2-x+b$
$=(x^2+x)(x^2-x+1)+a(x^2-x+1)+ax-a-x+b$
$=(x^2+x+a)(x^2-x+1)+x(a-1)+(b-a)$
Điều này nghĩa là: $x^4+ax^2+b$ chia $x^2-x+1$ dư $x(a-1)+(b-a)$
Để phép chia là chia hết thì $a-1=b-a=0$
$\Rightarrow a=b=1$


Bạn cần rút gọn đa thức nào thì nên ghi đầy đủ đa thức đó ra nhé.

Chiều dài của mảnh đất trồng rau: \(x-8\) (m)
Chiều rộng của mảnh đất trồng rau: \(x-12\left(m\right)\)
Diện tích của mảnh đất trồng rau: \(\left(x-8\right)\left(x-12\right)\left(m^2\right)\)
Ta có phương trình:
\(\left(x-8\right)\left(x-12\right)=96\)
\(\Leftrightarrow x^2-8x-12x+84=96\)
\(\Leftrightarrow x^2-20x+96-96=0\)
\(\Leftrightarrow x^2-20x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(ktm\right)\\x=20\left(tm\right)\end{matrix}\right.\)
Vậy độ dài của khu vườn là 20 m

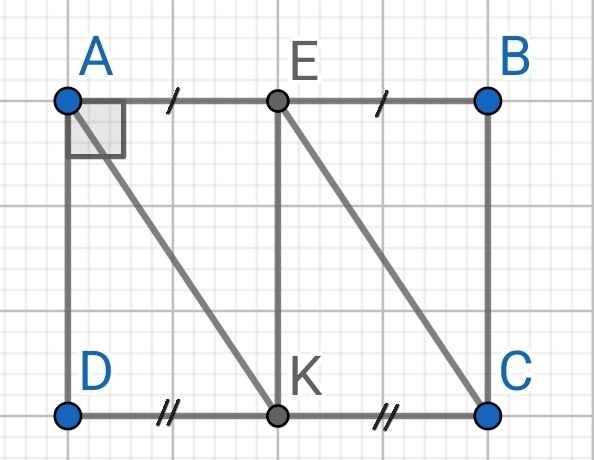 a) Do E là trung điểm của AB (gt)
a) Do E là trung điểm của AB (gt)
⇒ AE = AB : 2
Do K là trung điểm của CD (gt)
⇒ CK = DK = CD : 2
Mà AB = CD (do ABCD là hình chữ nhật)
⇒ AE = CK
Lại có AB // CD (do ABCD là hình chữ nhật)
⇒ AE // CK
Tứ giác AECK có:
AE // CK (cmt)
AE = CK (cmt)
⇒ AECK là hình bình hành
b) Do AE = AB : 2 (cmt)
DK = CD : 2 (cmt)
AB = CD (cmt)
⇒ AE = DK
Lại có:
AB // CD (cmt)
⇒ AE // DK
Tứ giác AEKD có:
AE // DK (cmt)
AE = DK (cmt)
⇒ AEKD là hình bình hành
Mà ∠EAK = 90⁰ (do ABCD là hình chữ nhật)
⇒ AEKD là hình chữ nhật
⇒ ∠AEK = 90⁰
Hay AE ⊥ EK

a) Ta thấy đa thức \(f\left(x\right)=4x^2+81\) vô nghiệm (*).
Giả sử \(f\left(x\right)\) có thể phân tích được thành nhân tử, khi đó \(f\left(x\right)=\left(ax+b\right)\left(cx+d\right)\), suy ra \(f\) có nghiệm là \(x=-\dfrac{b}{a}\) hoặc \(x=-\dfrac{d}{c}\), mâu thuẫn với (*).
Vậy ta không thể phân tích \(f\left(x\right)\) thành nhân tử.
b) \(g\left(x\right)=x^7+x^2+1\)
\(g\left(x\right)=x^7-x+x^2+x+1\)
\(g\left(x\right)=x\left(x^6-1\right)+\left(x^2+x+1\right)\)
\(g\left(x\right)=x\left(x^3-1\right)\left(x^3+1\right)+\left(x^2+x+1\right)\)
\(g\left(x\right)=x\left(x^3+1\right)\left(x-1\right)\left(x^2+x+1\right)+\left(x^2+x+1\right)\)
\(g\left(x\right)=\left(x^2+x+1\right)\left(x^5-x^4+x^2-x+1\right)\)
Xét \(h\left(x\right)=x^5-x^4+x^2-x+1\), nếu \(h\left(x\right)\) phân tích được thành nhân tử thì nó có nghiệm hữu tỉ. Khi đó nó có dạng \(x=\dfrac{p}{q},\left(p,q\inℤ;\left(p,q\right)=1\right),p|1,q|1\) \(\Rightarrow x=\pm1\). Ta thấy \(h\left(1\right).h\left(-1\right)\ne0\) nên 2 nghiệm này không thỏa mãn. Vậy h(x) không có nghiệm hữu tỉ \(\Rightarrow\) g(x) không thể phân tích tiếp.

\(x^2+4y^2+z^2-2x-6z+8y+14=0\\\Leftrightarrow (x^2-2x+1)+(4y^2+8y+4)+(z^2-6z+9)=0\\\Leftrightarrow (x^2-2\cdot x\cdot1+1^2)+[(2y)^2+2\cdot2y\cdot 2+2^2]+(z^2-2\cdot z\cdot3+3^2)=0\\\Leftrightarrow (x-1)^2+(2y+2)^2+(z-3)^2=0\)
Ta thấy: \(\left\{{}\begin{matrix}\left(x-1\right)^2\ge0\forall x\\\left(2y+2\right)^2\ge0\forall y\\\left(z-3\right)^2\ge0\forall z\end{matrix}\right.\)
\(\Rightarrow\left(x-1\right)^2+\left(2y+2\right)^2+\left(z-3\right)^2\ge0\forall x;y;z\)
Mặt khác: \(\left(x-1\right)^2+\left(2y+2\right)^2+\left(z-3\right)^2=0\)
nên ta được:
\(\left\{{}\begin{matrix}x-1=0\\2y+2=0\\z-3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\\z=3\end{matrix}\right.\)
Vậy: ...
\(x^2+4y^2+z^2-2x-6z+8y+14=0\)
\(\left(x^2-2x+1\right)+\left(4y^2+8y+4\right)+\left(z^2-6z+9\right)=0\)
\(\left(x-1\right)^2+\left(2y+2\right)^2+\left(z-3\right)^2=0\) (1)
Do \(\left(x-1\right)^2\ge0;\left(2y+2\right)^2\ge0;\left(z-3\right)^2\ge0\)
\(\left(1\right)\Rightarrow\) \(\left(x-1\right)^2=0;\left(2y+2\right)^2=0;\left(z-3\right)^2=0\)
*) \(\left(x-1\right)^2=0\)
\(x-1=0\)
\(x=1\)
*) \(\left(2y+2\right)^2=0\)
\(2y+2=0\)
\(2y=-2\)
\(y=-1\)
*) \(\left(z-3\right)^2=0\)
\(z-3=0\)
\(z=3\)
Vậy x = 1; y = -1; z = 3
a) Xem lại đề
b) x³ - 4x²y + 4xy² - 9x
= x(x² - 4xy + 4y² - 9)
= x[(x² - 4xy + 4y² - 3²]
= x[(x - 2y)² - 3²]
= x(x - 2y - 3)(x - 2y + 3)
c) x³ - y³ + x - y
= (x³ - y³) + (x - y)
= (x - y)(x² + xy + y²) + (x - y)
= (x - y)(x² + xy + y² + 1)
d) 4x² - 4xy + 2x - y + y²
= (4x² - 4xy + y²) + (2x - y)
= (2x - y)² + (2x - y)
= (2x - y)(2x - y + 1)
e) 9x² - 3x + 2y - 4y²
= (9x² - 4y²) - (3x - 2y)
= (3x - 2y)(3x + 2y) - (3x - 2y)
= (3x - 2y)(3x + 2y - 1)
f) 3x² - 6xy + 3y² - 5x + 5y
= (3x² - 6xy + 3y²) - (5x - 5y)
= 3(x² - 2xy + y²) - 5(x - y)
= 3(x - y)² - 5(x - y)
= (x - y)[(3(x - y) - 5]
= (x - y)(3x - 3y - 5)