A B C M N O H d

a/

Xét tg vuông AHO và tg vuông BHO có

AH=BH; OH chung => tg AHO = tg BHO (hai tg vuông có 2 cạnh góc vuông bằng nhau)

=> OA=OB (1)

=> tg OAB cân tại O \(\Rightarrow\widehat{OAB}=\widehat{OBA}\) (góc ở đáy tg cân) (2)

Ta có

AM+AN=AB (gt) => AN=AB-AM

BM=AB-AM

=> AN=BM (3)

Từ (1) (2) (3) => tg BOM = tg AON (c.g.c)

b/

Từ O dựng đường thẳng d vuông góc với MN

=> d là đường cao của tg OMN

Ta có

tg BOM = tg AON (cmt) => OM=ON => tg OMN cân tại O

=> d là đường trung trực của tg OMN hay d là đường trung trực của MN (Trong tg cân đường cao xuất phát từ đỉnh tg cân đồng thời là đường trung trực)

Ta có OH là đường trung trực của AB cố định; AO là đường phân giác của \(\widehat{A}\) không đổi => O cố dịnh

=> d luôn đi qua O cố định

Số chẵn là một số nguyên chia hết cho 2

Cảm ơn bạn nha

a: \(f\left(x\right)=2x^3+2x+x^2-2x^3-x+1\)

\(=\left(2x^3-2x^3\right)+x^2+2x-x+1=x^2+x+1\)

b: \(h\left(x\right)-f\left(x\right)=2x^2-x-1\)

=>\(h\left(x\right)=2x^2-x-1+x^2+x+1\)

=>\(h\left(x\right)=3x^2\)

c: \(f\left(x\right)\cdot\left(x-1\right)=\left(x^2+x+1\right)\left(x-1\right)\)

\(=x^3-x^2+x^2-x+x-1=x^3-1\)

Bài 2:

a: \(\dfrac{a}{5}=\dfrac{b}{7}\)

mà a-b=10

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{a}{5}=\dfrac{b}{7}=\dfrac{a-b}{5-7}=\dfrac{10}{-2}=-5\)

=>\(a=-5\cdot5=-25;b=-5\cdot7=-35\)

b: \(\dfrac{a}{-4}=\dfrac{b}{6}=\dfrac{c}{7}\)

mà a-2b+c=18

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{a}{-4}=\dfrac{b}{6}=\dfrac{c}{7}=\dfrac{a-2b+c}{-4-2\cdot6+7}=\dfrac{18}{-9}=-2\)

=>\(\left\{{}\begin{matrix}a=\left(-2\right)\cdot\left(-4\right)=8\\b=-2\cdot6=-12\\c=-2\cdot7=-14\end{matrix}\right.\)

Bài 3:

Gọi độ dài ba cạnh lần lượt là a(cm),b(cm),c(cm)

(Điều kiện: a>0; b>0; c>0)

Độ dài ba cạnh lần lượt tỉ lệ với 3;7;5 nên \(\dfrac{a}{3}=\dfrac{b}{7}=\dfrac{c}{5}\)

Chu vi tam giác là 105cm nên a+b+c=105

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{a}{3}=\dfrac{b}{7}=\dfrac{c}{5}=\dfrac{a+b+c}{3+7+5}=\dfrac{105}{15}=7\)

=>\(a=7\cdot3=21\left(nhận\right);b=7\cdot7=49\left(nhận\right);c=7\cdot5=35\left(nhận\right)\)

Vậy: Độ dài ba cạnh là 21cm; 49cm; 35cm

Bài 6

Em ghi đề sai rồi

Bài 7

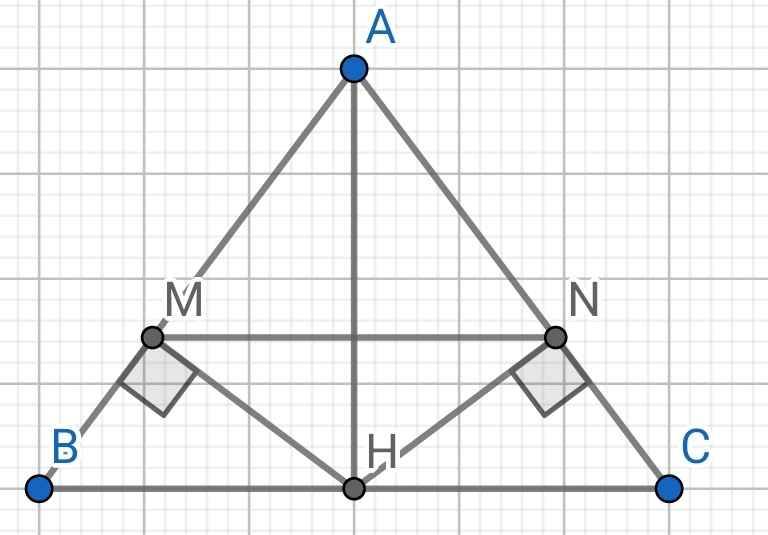
a) Do ∆ABC cân tại A (gt)

⇒ AB = AC

Do H là trung điểm của BC (gt)

⇒ HB = HC

Xét ∆ABH và ∆ACH có:

AB = AC (cmt)

AH là cạnh chung

HB = HC (cmt)

⇒ ∆ABH = ∆ACH (c-c-c)

⇒ ∠BAH = ∠CAH (hai góc tương ứng)

⇒ AH là tia phân giác của ∠BAC

b) Do ∠BAH = ∠CAH (cmt)

⇒ ∠MAH = ∠NAH

Xét hai tam giác vuông: ∆AHM và ∆AHN có:

AH là cạnh chung

∠MAH = ∠NAH (cmt)

⇒ ∆AHM = ∆AHN (cạnh góc vuông - góc nhọn kề)

⇒ AM = AN (hai cạnh tương ứng)

⇒ ∆AMN cân tại A

205: \(f\left(x\right)=x^2-x+1\)

\(=x^2-x+\dfrac{1}{4}+\dfrac{3}{4}\)

\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>=\dfrac{3}{4}>0\forall x\)

=>f(x) không có nghiệm thực

204:

a: \(f\left(-1\right)=\left(-1\right)^4+5\cdot\left(-1\right)^3+3\cdot\left(-1\right)^2+2\cdot\left(-1\right)+3\)

\(=1-5+3-2+3\)

=7-7=0

=>x=-1 là nghiệm của f(x)

\(g\left(-1\right)=3\cdot\left(-1\right)^4+\left(-1\right)^3+\left(-1\right)^2-7\cdot\left(-1\right)-10\)

\(=3-1+1+7-10=10-10=0\)

=>x=-1 là nghiệm của g(x)

\(h\left(-1\right)=4\cdot\left(-1\right)^3+2\cdot\left(-1\right)^2-\left(-1\right)+1\)

\(=-4+2+1+1=0\)

=>x=-1 là nghiệm của h(x)

khoảng 40-45

40-45 kg

Cho:

Điền hệ số thích hợp vào ô trống.
�(�)+�(�)=P(x)+Q(x)= ((�3x3)) ++ ((�2x2))++ ((�x)) ++ (())

P(x)+Q(x)

\(=3x^2-3x+6+4x^3-5x^2+x-3\)

\(=4x^3-2x^2-2x+3\)

a: Xét ΔAHB và ΔAHC có

AH chung

HB=HC

AB=AC

Do đó: ΔAHB=ΔAHC

b: Ta có: ΔAHB=ΔAHC

=>\(\widehat{BAH}=\widehat{CAH}\)

mà \(\widehat{BAH}=\widehat{CKA}\)(hai góc so le trong, BA//CK)

nên \(\widehat{CAK}=\widehat{CKA}\)

=>ΔCAK cân tại C

=>CA=CK

mà CA=BA

nên CK=BA

Ta có: ΔAHB=ΔAHC

=>\(\widehat{AHB}=\widehat{AHC}\)

mà \(\widehat{AHB}+\widehat{AHC}=180^0\)(hai góc kề bù)

nên \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\)

=>AH\(\perp\)BC

Ta có: ΔCAK cân tại C

mà CH là đường cao

nên H là trung điểm của AK

Xét ΔBAK có

BH là đường cao

BH là đường trung tuyến

Do đó: ΔBAK cân tại B

=>BA=BK

c: Đề sai rồi bạn

a: Xét ΔABD và ΔACD có

AB=AC

\(\widehat{BAD}=\widehat{CAD}\)

AD chung

Do đó: ΔABD=ΔACD

=>\(\widehat{ADB}=\widehat{ADC}\)

mà \(\widehat{ADB}+\widehat{ADC}=180^0\)

nên \(\widehat{ADB}=\widehat{ADC}=\dfrac{180^0}{2}=90^0\)

=>AD\(\perp\)BC

ta có: ΔABD=ΔACD

=>BD=CD

=>D là trung điểm của BC

mà AD\(\perp\)BC tại D

nên AD là đường trung trực của BC

b: 

Cách 1:

XétΔEDB vuông tại D và ΔEDC vuông tại E có

ED chung

DB=DC

Do đó: ΔEDB=ΔEDC

=>EB=EC

=>ΔEBC cân tại E

Cách 2:

Xét ΔEBC có

ED là đường cao

ED là đường trung tuyến

Do đó: ΔEBC cân tại E