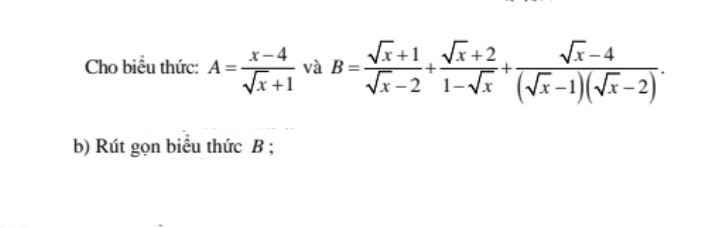
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số nghệ sỹ tham gia từ nơi khác đến là \(x\) (nghệ sỹ ; \(x\) \(\in\) N*
Số nghệ sỹ không chuyên tại Quảng Ninh là: \(x\) \(\times\) \(\dfrac{2}{3}\) (nghệ sỹ)
Theo bài ra ta có: \(x-200\) = \(x\times\) \(\dfrac{2}{3}\) + 200
\(x\) - \(x\times\) \(\dfrac{2}{3}\) = 400
\(x\) \(\times\) ( 1 - \(\dfrac{2}{3}\)) = 400
\(x\) \(\times\) \(\dfrac{1}{3}\) = 400
\(x\) = 400: \(\dfrac{1}{3}\)
\(x\) = 1200
Số nghệ sỹ không chuyên tại Quảng Ninh là:
1200 \(\times\) \(\dfrac{2}{3}\) = 800 (nghệ sỹ)
Tổng số nghệ sỹ tham gia tại buổi biểu diễn canarval là:
1200 + 800 = 2000 (nghệ sỹ)
Kết luận có 2000 nghệ sỹ đã tham gia buổi biểu diễn

Do số tam giác được lập từ n điểm đã cho là hữu hạn nên tồn tại 1 tam giác ABC có diện tích lớn nhất.
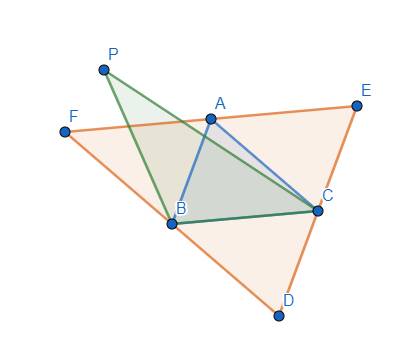
Dựng tam giác DEF sao cho A, B, C lần lượt là trung điểm của EF, DF, DE. Khi đó vì \(S_{ABC}\le1\) nên \(S_{DEF}\le4\). Ta sẽ chứng minh tam giác DEF chính là tam giác cần tìm.
Thật vậy, giả sử tồn tại điểm P trong số n điểm đã cho nằm ngoài tam giác DEF. Không mất tính tổng quát, giả sử P nằm khác phía BC đối với EF. Khi đó khoảng cách từ P đến BC sẽ lớn hơn khoảng cách từ A đến BC, dẫn đến \(S_{PBC}>S_{ABC}\), điều này là vô lí vì ta đã giả sử tam giác ABC là tam giác có diện tích lớn nhất trong số các tam giác tạo thành từ n điểm đã cho \(\Rightarrow\) tam giác DEF thỏa ycbt
Vậy ta có đpcm.
,
Nếu bạn không xem được phần trả lời của mình thì vào trang cá nhân của mình xem nhé, tại câu trả lời của mình có vẽ hình nên nó không đăng lên được ngay.

Gọi \(2n+1\) điểm đó là \(A_1,A_2,...,A_{2n+1}\). Do số điểm là hữu hạn nên tồn tại 1 đoạn thẳng \(A_iA_j\left(i\ne j\right)\) sao cho \(A_iA_j\) lớn nhất trong các \(A_kA_l\left(k\ne l;k,l=\overline{1,2n+1}\right)\).
TH1: Nếu \(A_iA_j\le1\), ta dựng 2 đường tròn \(\left(A_i,1cm\right)\) và \(\left(A_j,1cm\right)\). Dĩ nhiên nếu có bất kì điểm \(A_m\) nào nằm ngoài 2 đường tròn trên thì mâu thuẫn với giả thiết \(A_iA_j\) là đoạn thẳng có độ dài lớn nhất. Do đó, tất cả \(2n+1\) điểm sẽ nằm trong 2 đường tròn. Theo nguyên lí Dirichlet sẽ tồn tại 1 hình tròn chứa \(n+1\) điểm trong \(2n+1\) điểm đã cho. Đó là hình tròn cần tìm.
TH2: Nếu \(A_iA_j>1\), ta vẫn dựng 2 đường tròn \(\left(A_i,1cm\right)\) và \(\left(A_j,1cm\right)\). Khi đó nếu có bất kì điểm \(A_m\) nào nằm ở ngoài cả 2 hình tròn thì \(A_mA_i\) và \(A_mA_j\) đều lớn hơn 1. Khi đó bộ 3 điểm \(\left(A_i,A_j,A_m\right)\) mâu thuẫn với giả thiết trong 3 điểm bất kì luôn có 2 điểm có khoảng cách nhỏ hơn 1. Do vậy, tất cả các điểm đã cho đều nằm trong 2 đường tròn kể trên. Lại theo nguyên lí Dirichlet thì tồn tại \(n+1\) điểm thuộc cùng một hình tròn. Đấy chính là hình tròn cần tìm.
Vậy trong mọi trường hợp, ta đều tìm được 1 hình tròn bán kính 1cm chứa \(n+1\) điểm trong số \(2n+1\) điểm đã cho. Ta có đpcm.
Mình giải thích thêm trường hợp 1 nhé. Nếu như có 1 điểm \(A_m\) nằm ngoài 1 trong 2 đường tròn \(\left(A_i,1\right)\) và \(\left(A_j,1\right)\) thì 1 trong 2 đoạn \(A_mA_i\) và \(A_mA_j\) sẽ lớn hơn 1. Không mất tính tổng quát, giả sử đó là đoạn \(A_mA_i\). Khi đó \(A_mA_i>1\ge A_iA_j\), vô lí vì ta đã giả sử \(A_iA_j\) là đoạn có độ dài lớn nhất.

áp dụng
\(x^2+y^2\ge\dfrac{\left(x+y\right)^2}{2};\dfrac{1}{x^2}+\dfrac{1}{y^2}\ge\dfrac{1}{2}.\left(\dfrac{1}{x}+\dfrac{1}{y}\right)^2\)
\(\Rightarrow A\ge\dfrac{[\left(x+y\right)^2}{2}+z^2].\left(\dfrac{1}{2}.\left(\dfrac{1}{x}+\dfrac{1}{y}\right)^2+\dfrac{1}{z^2}\right)\)
áp dụng \(\dfrac{1}{x}+\dfrac{1}{y}\ge\dfrac{4}{x+y}\)
\(\Rightarrow A\ge[\dfrac{\left(x+y\right)^2}{2}+z^2].\left(\dfrac{1}{2}.\left(\dfrac{4}{x+y}\right)^2+\dfrac{1}{z^2}\right)=[\dfrac{\left(x+y\right)^2}{2}+z^2].\left(\dfrac{8}{\left(x+y\right)^2}+\dfrac{1}{z^2}\right)=4+1+\dfrac{\left(x+y\right)^2}{2z^2}+\dfrac{8z^2}{\left(x+y\right)^2}=5+\left(\dfrac{\left(x+y\right)^2}{2z^2}+\dfrac{z^2}{2\left(x+y\right)^2}\right)+\dfrac{15z^2}{2\left(x+y\right)^2}\ge5+2.\sqrt{\dfrac{1}{2}.\dfrac{1}{2}}+\dfrac{15\left(x+y\right)^2}{2.\left(x+y\right)^2}=5+1+\dfrac{15}{2}=\dfrac{27}{2}\)
dbxr<=>y=x=z/2>0

Ta thấy \(ab\le\dfrac{a^2+b^2}{2}=1\) và \(a+b\le\sqrt{2\left(a^2+b^2\right)}=2\). Áp dụng BĐT B.C.S, ta được \(P=\dfrac{a^4}{ba^2+a^2}+\dfrac{b^4}{ab^2+b^2}\) \(\ge\dfrac{\left(a^2+b^2\right)^2}{ba^2+ab^2+a^2+b^2}=\dfrac{2^2}{ab\left(a+b\right)+2}\ge\dfrac{4}{1.2+2}=1\)
ĐTXR \(\Leftrightarrow a=b=1\)
Vậy GTNN của P là 1 khi \(a=b=1\)
\(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}+\dfrac{\sqrt{x}+2}{1-\sqrt{x}}+\dfrac{\sqrt{x}-4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}\left(x\ge1\right)\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-\dfrac{\sqrt{x}+2}{\sqrt{x}-1}+\dfrac{\sqrt{x}-4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}-\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}-4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x-1-\left(x-4\right)+\sqrt{x}-4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x-1-x+4+\sqrt{x}-4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}-1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\\ =\dfrac{1}{\sqrt{x}-2}\)