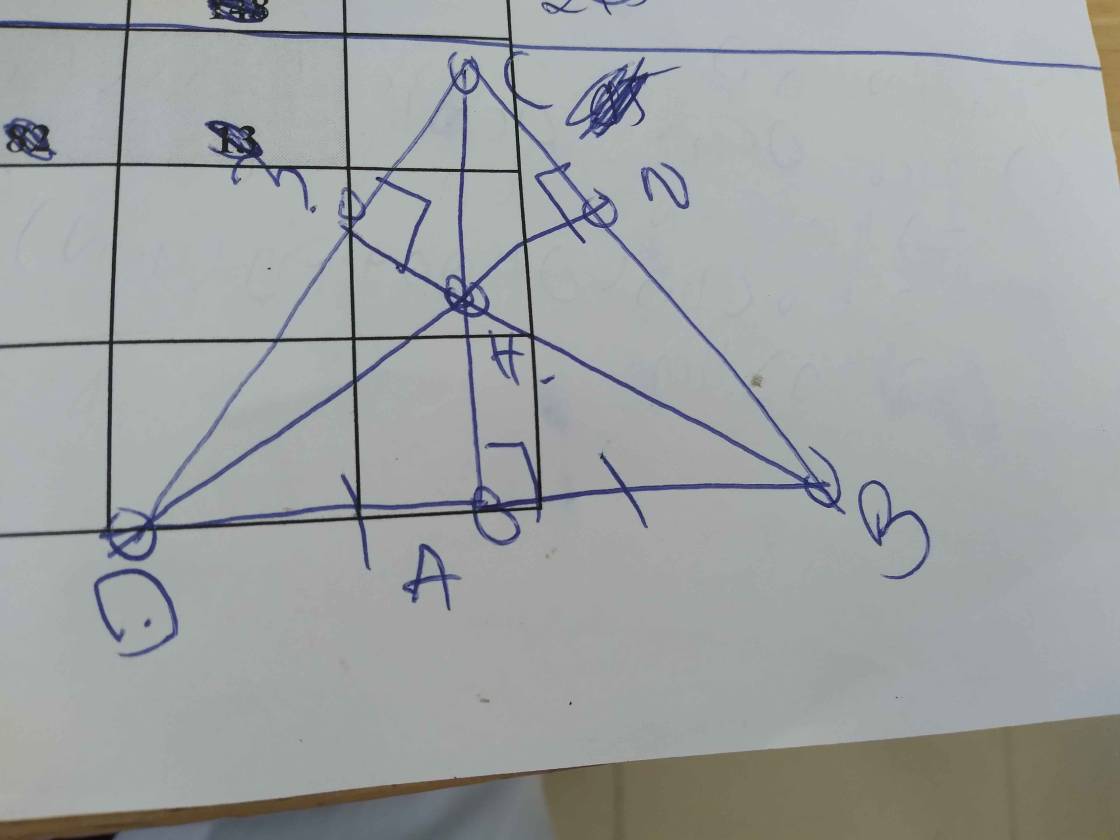
cho tam giác ABC vuông tại A,AB<AC.Lấy điểm D sao cho A là trung điểm của BD.a)Chứng minh CA là tia phân giác của góc BCD;b)Vẽ BM vuông góc với DC tại M,BM cắt AC tại H.Vẽ HN vuông góc với BC tại N.Chứng minh tam giác CMN cân và MN//BD;c)So sánh HB và HM
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Để chứng minh rằng \( BM = CN \), chúng ta sẽ sử dụng tính chất của tam giác cân.
Vì tam giác \( ABC \) cân tại \( A \), nên ta có \( AM = MC \) và \( AN = NB \), vì \( M \) là trung điểm của \( AC \) và \( N \) là trung điểm của \( AB \).
Bây giờ, ta cần chứng minh \( BM = CN \).
Ta có thể sử dụng định lí đối xứng của tam giác để chứng minh điều này.
Xét tam giác \( AMC \) và \( ANB \):
- \( AM = MC \) (vì \( M \) là trung điểm của \( AC \))
- \( AN = NB \) (vì \( N \) là trung điểm của \( AB \))
- \( AC = AB \) (vì tam giác \( ABC \) cân tại \( A \))
Theo định lí đối xứng của tam giác, ta có \( BM = CN \), vì hai tam giác \( AMC \) và \( ANB \) là đối xứng với nhau qua đường trung tuyến \( MN \).
Do đó, \( BM = CN \).


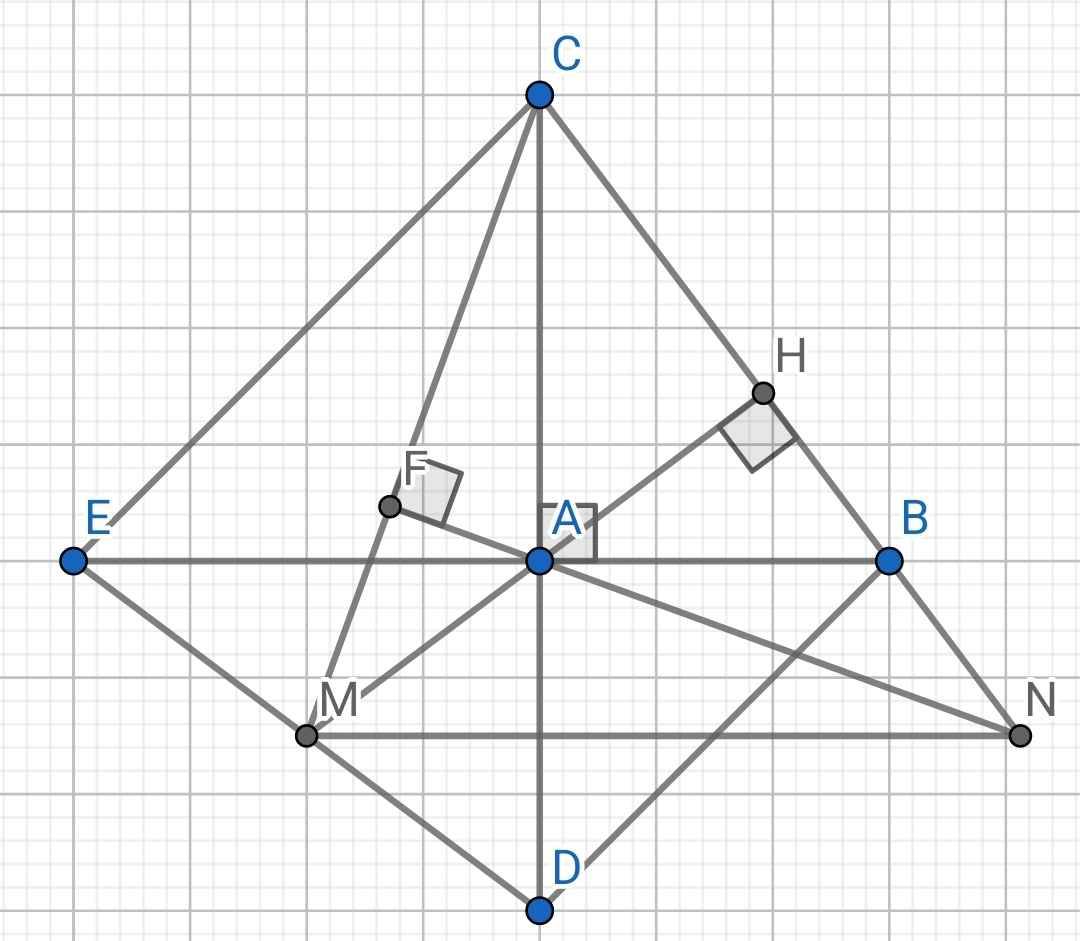
a) Do ∆ADB vuông cân tại A (gt)
⇒ AB = AD
Do ∆AEC vuông cân tại A (gt)
⇒ AE = AC
Xét hai tam giác vuông: ∆ABC và ∆ADE có:
AB = AD (cmt)
AC = AE (cmt)
∆ABC = ∆ADE (hai cạnh góc vuông)
⇒ BC = DE (hai cạnh tương ứng)
b) Do ∆ADE vuông cân tại A (gt)
⇒ ∠ADB = ∠ABD = 45⁰
Do ∆AEC vuông cân tại A (gt)
⇒ ∠ACE = ∠AEC = 45⁰
⇒ ∠ACE = ∠ADB = 45⁰
Mà ∠ACE và ∠ADB là hai góc so le trong
⇒ DB // EC
c) Do AH ⊥ BC (gt)
⇒ MH ⊥ CN
Do AF ⊥ MC (gt)
⇒ NF ⊥ MC
∆CMN có:
MH ⊥ CN (cmt)
NF ⊥ MC (cmt)
⇒ MH và NF là hai đường cao của ∆CMN
Mà MH cắt NF tại A
⇒ CA là đường cao thứ ba của ∆CMN
⇒ CA ⊥ MN
d) Em xem lại đề nhé

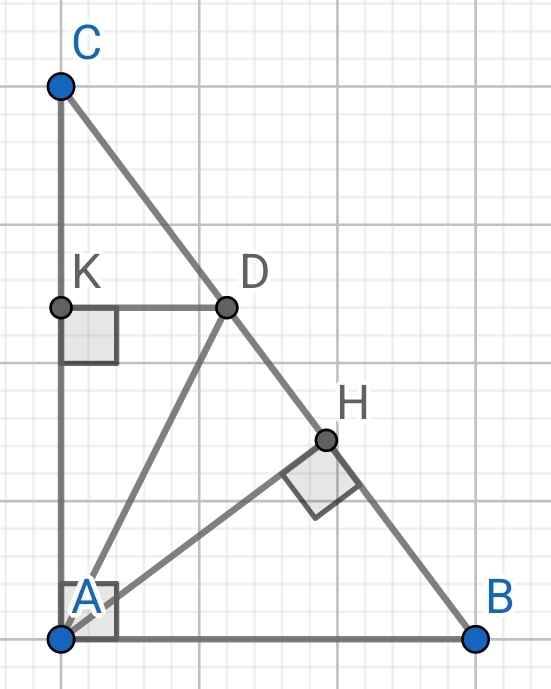
a) ∆ABD có:
BA = BD (gt)
⇒ ∆ABD cân tại B
⇒ ∠BAD = ∠BDA
b) Do DK ⊥ AC (gt)
AB ⊥ AC (do ∆ABC vuông tại A)
⇒ DK // AB
⇒ ∠ADK = ∠BAD (so le trong)
Mà ∠BAD = ∠BDA (cmt)
⇒ ∠ADK = ∠BDA
⇒ ∠ADK = ∠HDA
Xét hai tam giác vuông: ∆ADK và ∆ADH có:
AD là cạnh chung
∠ADK = ∠HDA (cmt)
⇒ ∆ADK = ∆ADH (cạnh huyền - góc nhọn)
⇒ ∠DAK = ∠DAH (hai góc tương ứng)
⇒ ∠DAC = ∠DAH
⇒ AD là tia phân giác của ∠HAC
c) Do ∆ADK = ∆ADH (cmt)
⇒ AK = AH (hai cạnh tương ứng)
d) ∆CDK vuông tại K
⇒ CD là cạnh huyền nên là cạnh lớn nhất
⇒ CK < CD
Mà AK = AH (cmt)
BA = BD (cmt)
Cộng vế với vế, ta có:
CK + AK + AB < CD + AH + BD
⇒ AB + AC < BC + AH
a: Xet ΔBAD có BA=BD
nên ΔBAD cân tại B
=>\(\widehat{BAD}=\widehat{BDA}\)
b: Ta có: \(\widehat{HAD}+\widehat{BDA}=90^0\)(ΔDHA vuông tại H)
\(\widehat{DAC}+\widehat{BAD}=90^0\)
mà \(\widehat{BDA}=\widehat{BAD}\)
nên \(\widehat{HAD}=\widehat{DAC}\)
=>AD là phân giác của góc HAC
c: Xét ΔAHD vuông tại H và ΔAKD vuông tại K có
AD chung
\(\widehat{HAD}=\widehat{KAD}\)
Do đó: ΔAHD=ΔAKD
=>AH=AK
d: Xét ΔABC có AH là đường cao
nên \(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{1}{2}\cdot AB\cdot AC\)
=>\(AH\cdot BC=AB\cdot AC\)
\(\left(AB+AC\right)^2-\left(BC+AH\right)^2\)
\(=AB^2+AC^2+2\cdot AB\cdot AC-BC^2-AH^2-2\cdot BC\cdot AH\)
\(=BC^2+2\cdot AH\cdot BC-BC^2-2\cdot BC\cdot AH-AH^2\)
\(=-AH^2< 0\)
=>\(\left(AB+AC\right)^2< \left(BC+AH\right)^2\)
=>AB+AC<BC+AH


a: \(M\left(x\right)=x^2-3x+5x^4-mx-3\)
\(=5x^4+x^2+x\left(-m-3\right)-3\)
\(=5x^4+x^2+x\left(-m-3\right)-3\)
b: Hệ số cao nhất của M(x) là 2 nên \(5=2\)(vô lý)
=>\(m\in\varnothing\)

M(\(x\)) = \(x^2\) - 3\(x\) + 5\(x^4\) - 2\(x^2\) - m\(x\) - 3
M(\(x\)) = 5\(x^4\) + (\(x^2\) - 2\(x^2\)) - (3\(x\) + m\(x\)) - 3
M(\(x\)) = 5\(x^4\) - \(x^2\) - \(x\)(3 + m) - 3
Bậc của đa thức M(\(x\)) là 4
Hệ số cao nhất là 5

a: Xét ΔANB và ΔENM có
NA=NE
\(\widehat{ANB}=\widehat{ENM}\)(hai góc đối đỉnh)
NB=NM
Do đó: ΔANB=ΔENM
b: Ta có: \(AB=\dfrac{BC}{2}\)
\(BM=MC=\dfrac{BC}{2}\)
Do đó: AB=BM=MC
mà ME=AB(ΔNAB=ΔNEM)
nên MC=ME
=>ΔMEC cân tại M
c: N là trung điểm của MB
=>\(BN=NM=\dfrac{BM}{2}=\dfrac{CM}{2}\)
\(CM+MN=CN\)
=>\(CN=CM+\dfrac{1}{2}CM=\dfrac{3}{2}CM\)
=>\(CM=\dfrac{2}{3}CN\)
Xét ΔCAE có
CN là đường trung tuyến
\(CM=\dfrac{2}{3}CN\)
Do đó: M là trọng tâm của ΔCAE
d: Xét ΔAEC có
M là trọng tâm
EM cắt AC tại D
Do đó: D là trung điểm của AC