tìm x
(x+2)(x2-2x+4)-x(x+3)3=8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
a. Xét tam giác $AME$ và $AHE$ có:
$AE$ chung
$\widehat{AEM}=\widehat{AEH}=90^0$
$ME=HE$ (gt)
$\Rightarrow \triangle AME=\triangle AHE$(c.g.c)
$\Rightarrow AM=AH(1)$
Hoàn toàn tương tự ta có $\triangle AHF=\triangle ANF$ (c.g.c)
$\Rightarrow AH=AN(2)$
Từ $(1); (2)\Rightarrow AM=AN$ nên tam giác $AMN$ là tam giác cân tại $A$.
b.
Ta có:
$\frac{HE}{EM}=\frac{HF}{FN}=1$ nên theo định lý Talet thì $EF\parallel MN$
c.
Vì tam giác $AMN$ cân tại $A$ (cm ở phần a) nên trung tuyến $AI$ đồng thời là đường cao.
$\Rightarrow AI\perp MN$
Mà $MN\parallel EF$
$\Rightarrow AI\perp EF$ (đpcm)


x²y + xy² - x - y
= (x²y + xy²) - (x + y)
= xy(x + y) - (x + y)
= (x + y)(xy - 1)

a) Ta tính tổng số các cặp lớp phân biệt có thể xảy ra.
Vị trí đầu tiên có \(x\) cách chọn và vị trí thứ hai sẽ có \(x-1\) cách chọn (do một lớp bất kì không thể đấu với chính lớp đó). Nhưng nếu tính như trên, thì mỗi trận đấu giữa 2 đội bất kì sẽ bị lặp lại thêm 1 lần, nên tổng số trận đấu khác nhau là \(\dfrac{x\left(x-1\right)}{2}\)
b) Cho \(\dfrac{x\left(x-1\right)}{2}=105\)
\(\Leftrightarrow x^2-x-210=0\)
\(\Leftrightarrow\left(x-21\right)\left(x+20\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=21\left(nhận\right)\\x=-20\left(loại\right)\end{matrix}\right.\)
Vậy có 21 đội tham gia.

Với \(x\ne0;x\ne\pm1;x\ne\dfrac{5}{2}\), ta có:
\(M=\left(\dfrac{3}{x-1}-\dfrac{7}{x+1}\right):\dfrac{-4x+10}{x\left(x+1\right)}\)
\(=\left[\dfrac{3\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}-\dfrac{7\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}\right]\cdot\dfrac{x\left(x+1\right)}{-4x+10}\)
\(=\dfrac{3x+3-7x+7}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x\left(x+1\right)}{-4x+10}\)
\(=\dfrac{-4x+10}{x-1}\cdot\dfrac{x}{-4x+10}\)
\(=\dfrac{x}{x-1}\)
\(Toru\)

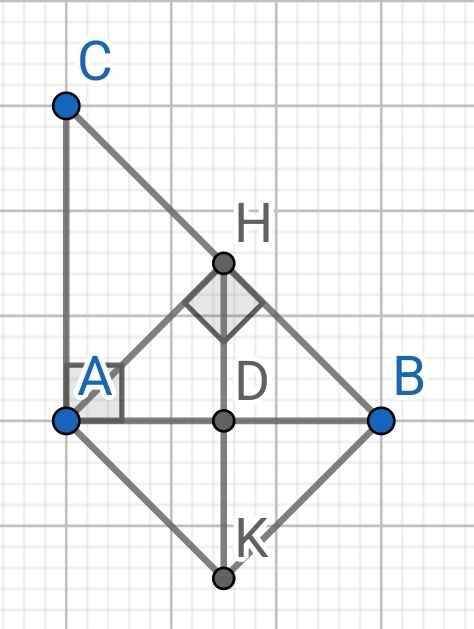
Do AH ⊥ BC (gt)
⇒ AH ⊥ BH
Do ∆ABC vuông cân tại A (gt)
AH là đường cao
⇒ AH cũng là đường trung tuyến của ∆ABC
⇒ H là trung điểm của BC
Gọi D là giao điểm của AB và HK
Do H và K đối xứng nhau qua AB (gt)
⇒ D là trung điểm của HK và AB là đường trung trực của HK
⇒ HK ⊥ AB
Mà AB ⊥ AC
⇒ HK // AC
⇒ HD // AC
Mà H là trung điểm của BC
⇒ D là trung điểm AB
Do ∆ABC vuông cân tại A (gt)
AH là đường trung tuyến của ∆ABC (cmt)
⇒ AH = HB = HC = BC : 2
Tứ giác AHBK có:
D là trung điểm HK (cmt)
D là trung điểm AB (cmt)
⇒ AHBK là hình bình hành
Mà AH ⊥ BH (cmt)
⇒ AHBK là hình chữ nhật
Lại có AH = BH (cmt)
⇒ AHBK là hình vuông
bbbbbbbbbbbbffv
Đề là $x(x+3)^3$ hay $x(x+3)^2$ hả bạn?