Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{2x^3-24x-20}{x^2+4x+3}\)
\(=\dfrac{2x^3+8x^2+6x-8x^2-32x-24x+2x-20}{x^2+4x+3}\)
\(=2x^2-8x+\dfrac{2x-20}{x^2+4x+3}\)

a: Nửa chu vi mảnh vườn là 90:2=45(m)
Chiều rộng mảnh vườn là 45-x(m)
Diện tích mảnh vườn là \(x\left(45-x\right)=45x-x^2\left(m^2\right)\)
b: Khi x=30 thì diện tích mảnh vườn là:
\(45\cdot30-30^2=1350-900=450\left(m^2\right)\)

a: Xét ΔCAE vuông tại A và ΔCDE vuông tại D có
CE chung
\(\widehat{ACE}=\widehat{DCE}\)
Do đó: ΔCAE=ΔCDE
=>\(\widehat{AEC}=\widehat{DEC}\)
=>EC là phân giác của góc AED
b: Ta có: ΔCAE=ΔCDE
=>CA=CD và EA=ED
Ta có: CA=CD
=>C nằm trên đường trung trực của AD(1)
Ta có: EA=ED
=>E nằm trên đường trung trực của AD(2)
Từ (1),(2) suy ra CE là đường trung trực của AD
c: Ta có: \(\widehat{CIH}+\widehat{ICH}=90^0\)(ΔCHI vuông tại H)
\(\widehat{CEA}+\widehat{ACE}=90^0\)(ΔCAE vuông tại A)
mà \(\widehat{ICH}=\widehat{ACE}\)
nên \(\widehat{CIH}=\widehat{CEA}\)
=>\(\widehat{AEI}=\widehat{AIE}\)
=>ΔAIE cân tại A

Bài 2:
a: Đặt A(x)=0
=>\(\left(2x+3\right)\left(x-1\right)-2x\left(x+3\right)=0\)
=>\(2x^2-2x+3x-3-2x^2-6x=0\)
=>-5x-3=0
=>-5x=3
=>\(x=-\dfrac{3}{5}\)
b: Đặt B(x)=0
=>\(9x^3-x=0\)
=>\(x\left(9x^2-1\right)=0\)
=>x(3x-1)(3x+1)=0
=>\(\left[{}\begin{matrix}x=0\\x=\dfrac{1}{3}\\x=-\dfrac{1}{3}\end{matrix}\right.\)
c: Đặt C(x)=0
=>\(\left(x^2+1\right)\left(x^2-3\right)=0\)
mà \(x^2+1>0\forall x\)
nên \(x^2-3=0\)
=>\(x^2=3\)
=>\(x=\pm\sqrt{3}\)
Câu 1:
a: \(A\left(x\right)=x^4-3x^3-3x^4+2x^3-x^2+2x-5\)
\(=\left(x^4-3x^4\right)+\left(-3x^3+2x^3\right)-x^2+2x-5\)
\(=-2x^4-x^3-x^2+2x-5\)
\(B\left(x\right)=2x^4+x^2-3x^3-2x\left(x-1\right)\)
\(=2x^4-3x^3+x^2-2x^2+2x\)
\(=2x^4-3x^3-x^2+2x\)
b: A(x)+B(x)
\(=-2x^4-x^3-x^2+2x-5+2x^4-3x^3-x^2+2x\)
\(=-4x^3-2x^2+4x-5\)
A(x)-B(x)
\(=-2x^4-x^3-x^2+2x-5-2x^4+3x^3+x^2-2x\)
\(=-4x^4+2x^3-5\)
c: \(B\left(1\right)=2\cdot1^4-3\cdot1^3-1^2+2\cdot1=2-3-1+2=0\)

Bài 1:
Gọi số quyển sách của An,Bình,Cường lần lượt là a(quyển),b(quyển),c(quyển)
(ĐK: \(a,b,c\in Z^+\))
Số quyển sách của An,Bình, Cường lần lượt tỉ lệ với 3;4;5 nên \(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}\)
Số sách của Bình ít hơn tổng số sách của An và Cường là 8 quyển nên a+c-b=8
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+c-b}{3+5-4}=\dfrac{8}{4}=2\)
=>\(a=2\cdot3=6;b=2\cdot4=8;c=2\cdot5=10\)
Vậy: số quyển sách của An,Bình,Cường lần lượt là 6 quyển; 8 quyển; 10 quyển
Bài 2:
a: Biến cố chắc chắn là B
Biến cố không thể là C
b: Biến cố A:"lấy được số là số nguyên tố"
=>A={5}
=>n(A)=1
\(P\left(A\right)=\dfrac{1}{5}\)
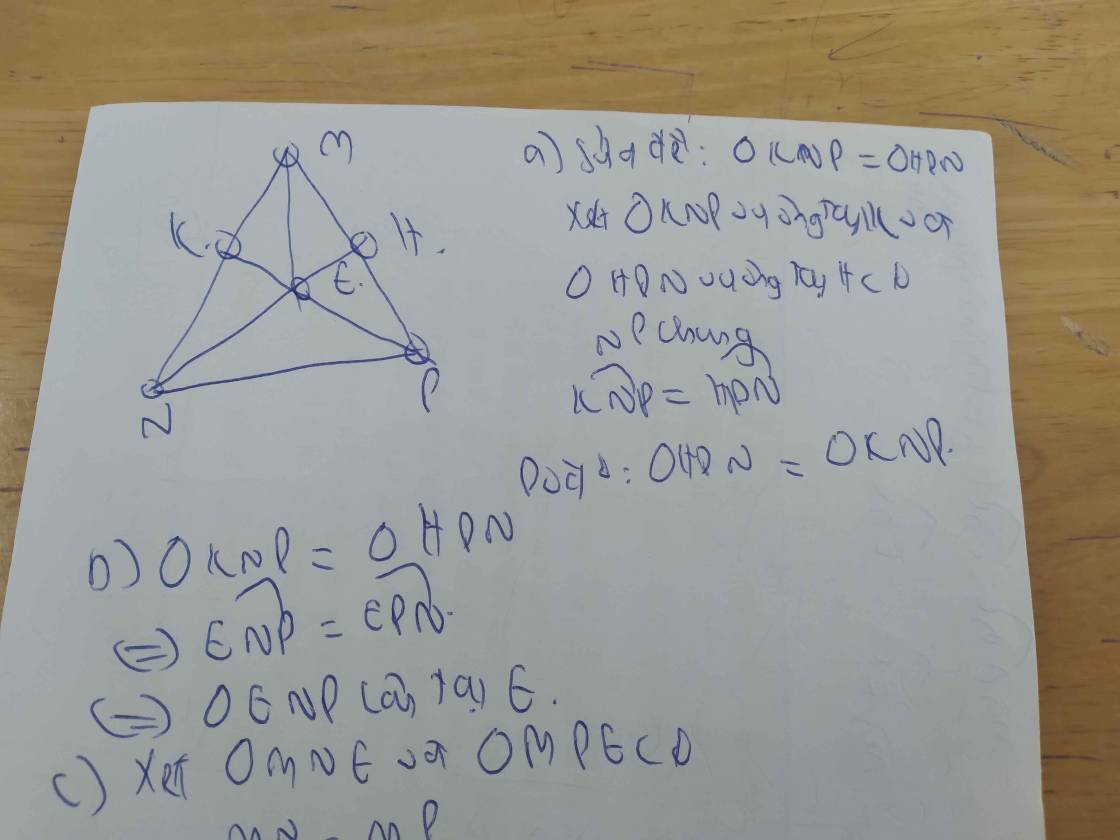




A = (xⁿ + 1)(xⁿ - 2) - xⁿ⁻³(xⁿ⁺³ - x³) + 2007
= x²ⁿ - 2xⁿ + xⁿ - 2 - x²ⁿ - xⁿ + 2007
= (x²ⁿ - x²ⁿ) + (xⁿ - xⁿ) + (-2 + 2007)
= 2005
Vậy giá trị của A không phụ thuộc váo giá trị của x